Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10 tập 2 Kết nối tri thức. Mục 3 trang 85, 86 tập trung vào các kiến thức quan trọng về vectơ, phép toán vectơ và ứng dụng của chúng trong hình học.
Chúng tôi hiểu rằng việc tự học Toán đôi khi gặp nhiều khó khăn. Vì vậy, đội ngũ gia sư giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn bộ giải bài tập này với mục tiêu giúp bạn nắm vững kiến thức và tự tin giải quyết mọi bài toán.
Có ba hộp A, B, C. Hộp A có chứa ba thẻ mang số 1, số 2 và số 3. Hộp B chứa hai thẻ mang số 2 và số 3. Hộp C chứa hai thẻ mang số 1 và số 2. Từ mỗi hộp ta rút ra ngẫu nhiên một thẻ.
Cho E là một biến cố và \(\Omega \) là không gian mẫu. Tính n(\(\overline E \)) theo n(\(\Omega \)) và n(E).
Lời giải chi tiết:
Ta có \(n\left( {\overline E } \right) = n\left( \Omega \right) - n\left( E \right)\).
Giải bài toán trong tình huống mở đầu.
Lời giải chi tiết:
Ta có \(P\left( F \right) = \frac{{n\left( F \right)}}{{n\left( \Omega \right)}} = \frac{1}{{C_{45}^6}} = \frac{1}{{8145060}}\) và \(P\left( G \right) = \frac{{n\left( G \right)}}{{n\left( \Omega \right)}} = \frac{{234}}{{C_{45}^6}} = \frac{{39}}{{1357510}}\).
Cho E là một biến cố và \(\Omega \) là không gian mẫu. Tính n(\(\overline E \)) theo n(\(\Omega \)) và n(E).
Lời giải chi tiết:
Ta có \(n\left( {\overline E } \right) = n\left( \Omega \right) - n\left( E \right)\).
Có ba hộp A, B, C. Hộp A có chứa ba thẻ mang số 1, số 2 và số 3. Hộp B chứa hai thẻ mang số 2 và số 3. Hộp C chứa hai thẻ mang số 1 và số 2. Từ mỗi hộp ta rút ra ngẫu nhiên một thẻ.
a) Vẽ sơ đồ hình cây để mô tả các phần tử của không gian mẫu.
b) Gọi M là biến cố: “Trong ba thẻ rút ra có ít nhất một thẻ số 1". Biến cố \(\overline M \) là tập con nào của không gian mẫu?
c) Tính P(M) và P(\(\overline M \)).
Lời giải chi tiết:
a) Vẽ sơ đồ cây ba tầng.
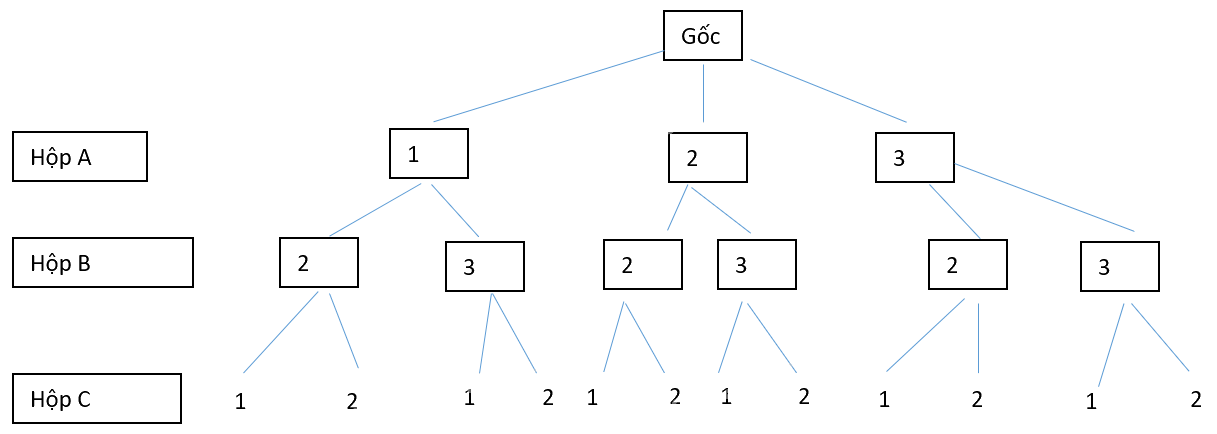
b) Chuyển qua biến cố đối: Từ sơ đồ cây xác định không gian mẫu và biến cố \(\overline M \): “Trong ba thẻ rút ra không có thẻ số 1”.
\(\begin{array}{l}\overline M = \left\{ {222;232;322;332} \right\}\\c, n(\overline M ) = 4\\P(\overline M ) = \frac{{n(\overline M )}}{{n(\Omega )}} = \frac{4}{{12}} = \frac{1}{3}\\ \Rightarrow P(M) = 1 - P(\overline M ) = 1 - \frac{1}{3} = \frac{2}{3}\end{array}\)
Giải bài toán trong tình huống mở đầu.
Lời giải chi tiết:
Ta có \(P\left( F \right) = \frac{{n\left( F \right)}}{{n\left( \Omega \right)}} = \frac{1}{{C_{45}^6}} = \frac{1}{{8145060}}\) và \(P\left( G \right) = \frac{{n\left( G \right)}}{{n\left( \Omega \right)}} = \frac{{234}}{{C_{45}^6}} = \frac{{39}}{{1357510}}\).
Có ba hộp A, B, C. Hộp A có chứa ba thẻ mang số 1, số 2 và số 3. Hộp B chứa hai thẻ mang số 2 và số 3. Hộp C chứa hai thẻ mang số 1 và số 2. Từ mỗi hộp ta rút ra ngẫu nhiên một thẻ.
a) Vẽ sơ đồ hình cây để mô tả các phần tử của không gian mẫu.
b) Gọi M là biến cố: “Trong ba thẻ rút ra có ít nhất một thẻ số 1". Biến cố \(\overline M \) là tập con nào của không gian mẫu?
c) Tính P(M) và P(\(\overline M \)).
Lời giải chi tiết:
a) Vẽ sơ đồ cây ba tầng.
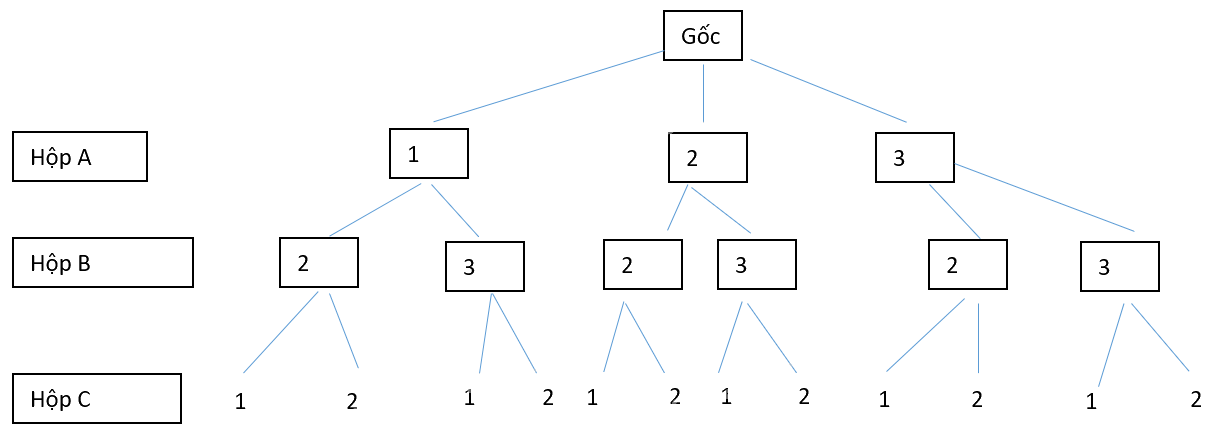
b) Chuyển qua biến cố đối: Từ sơ đồ cây xác định không gian mẫu và biến cố \(\overline M \): “Trong ba thẻ rút ra không có thẻ số 1”.
\(\begin{array}{l}\overline M = \left\{ {222;232;322;332} \right\}\\c, n(\overline M ) = 4\\P(\overline M ) = \frac{{n(\overline M )}}{{n(\Omega )}} = \frac{4}{{12}} = \frac{1}{3}\\ \Rightarrow P(M) = 1 - P(\overline M ) = 1 - \frac{1}{3} = \frac{2}{3}\end{array}\)
Mục 3 của SGK Toán 10 tập 2 Kết nối tri thức tập trung vào việc củng cố và mở rộng kiến thức về vectơ. Các bài tập trong mục này yêu cầu học sinh vận dụng các định nghĩa, tính chất của vectơ, các phép toán vectơ (cộng, trừ, nhân với một số thực) và ứng dụng của vectơ trong việc giải quyết các bài toán hình học.
Bài 1 thường bao gồm các câu hỏi trắc nghiệm và bài tập tự luận nhằm kiểm tra mức độ hiểu biết của học sinh về khái niệm vectơ, các yếu tố của vectơ, và các phép toán cơ bản trên vectơ. Việc nắm vững các định nghĩa và tính chất là chìa khóa để giải quyết thành công các bài tập trong bài này.
Bài 2 đi sâu vào các phép toán cộng, trừ vectơ, nhân vectơ với một số thực. Học sinh cần hiểu rõ các quy tắc thực hiện các phép toán này và biết cách áp dụng chúng để giải quyết các bài toán cụ thể. Các bài tập thường yêu cầu học sinh tính toán các phép toán vectơ, chứng minh các đẳng thức vectơ, và tìm các vectơ thỏa mãn các điều kiện cho trước.
Bài 3 tập trung vào việc ứng dụng vectơ để giải quyết các bài toán hình học, chẳng hạn như chứng minh các tính chất của hình bình hành, hình thang, và các hình đa giác khác. Học sinh cần biết cách biểu diễn các điểm, vectơ, và các đường thẳng bằng phương trình vectơ, và sử dụng các phương trình này để giải quyết các bài toán hình học.
Giaitoan.edu.vn cung cấp lời giải chi tiết cho từng bài tập trong mục 3 trang 85, 86 SGK Toán 10 tập 2 Kết nối tri thức. Lời giải được trình bày một cách rõ ràng, dễ hiểu, và có kèm theo các hình vẽ minh họa để giúp học sinh dễ dàng theo dõi và nắm bắt kiến thức. Ngoài ra, chúng tôi cũng cung cấp các lời giải khác nhau cho cùng một bài tập để giúp học sinh có thêm nhiều góc nhìn và lựa chọn.
Bài tập: Cho tam giác ABC. Gọi M là trung điểm của BC. Chứng minh rằng AB + AC = 2AM.
Lời giải:
Để học tốt môn Toán 10, bạn có thể tham khảo thêm các tài liệu sau:
Hy vọng rằng với lời giải chi tiết và các hướng dẫn hữu ích trên đây, bạn sẽ tự tin giải quyết các bài tập trong mục 3 trang 85, 86 SGK Toán 10 tập 2 Kết nối tri thức. Chúc bạn học tập tốt!