Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10 Kết nối tri thức. Bài viết này sẽ hướng dẫn bạn giải bài 14 trang 96 SGK Toán 10 một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những phương pháp giải toán đơn giản, dễ tiếp thu, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
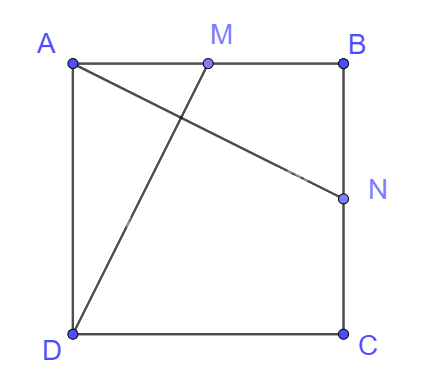
Cho hình vuông ABCD có cạnh bằng a. Gọi M, N tương ứng là trung điểm của các cạnh AB, BC.
Đề bài
Cho hình vuông ABCD có cạnh bằng a. Gọi M, N tương ứng là trung điểm của các cạnh AB, BC.
a) Biểu thị các vecto \(\overrightarrow {DM} ,\overrightarrow {AN} \) theo các vecto \(\overrightarrow {AB} ,\overrightarrow {AD} \)
b) Tính \(\overrightarrow {DM} .\overrightarrow {AN} \) và tìm góc giữa hai đường thẳng DM và AN.
Lời giải chi tiết
a) Ta có:
\(\overrightarrow {DM} = \overrightarrow {DA} + \overrightarrow {AM} = - \overrightarrow {AD} + \frac{1}{2}\overrightarrow {AB} \) (do M là trung điểm của AB)
\(\overrightarrow {AN} = \overrightarrow {AB} + \overrightarrow {BN} = \overrightarrow {AB} + \frac{1}{2}\overrightarrow {BC} = \overrightarrow {AB} + \frac{1}{2}\overrightarrow {AD} \) (do N là trung điểm của BC)
b)
\(\begin{array}{l}\overrightarrow {DM} .\overrightarrow {AN} = \left( { - \overrightarrow {AD} + \frac{1}{2}\overrightarrow {AB} } \right).\left( {\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AD} } \right)\\ = - \overrightarrow {AD} .\overrightarrow {AB} - \frac{1}{2}{\overrightarrow {AD} ^2} + \frac{1}{2}{\overrightarrow {AB} ^2} + \frac{1}{4}\overrightarrow {AB} .\overrightarrow {AD} \end{array}\)
Mà \(\overrightarrow {AB} .\overrightarrow {AD} = \overrightarrow {AD} .\overrightarrow {AB} = 0\) (do \(AB \bot AD\)), \({\overrightarrow {AB} ^2} = A{B^2} = {a^2};{\overrightarrow {AD} ^2} = A{D^2} = {a^2}\)
\( \Rightarrow \overrightarrow {DM} .\overrightarrow {AN} = - 0 - \frac{1}{2}{a^2} + \frac{1}{2}{a^2} + \frac{1}{4}.0 = 0\)
Vậy \(DM \bot AN\) hay góc giữa hai đường thẳng DM và AN bằng \({90^ \circ }\).
Bài 14 trang 96 SGK Toán 10 – Kết nối tri thức thuộc chương trình học về vectơ trong mặt phẳng. Bài tập này yêu cầu học sinh vận dụng kiến thức về tích vô hướng của hai vectơ để giải quyết các bài toán liên quan đến góc giữa hai vectơ, độ dài vectơ và các ứng dụng thực tế.
Bài 14 bao gồm các dạng bài tập sau:
Để giải các bài tập về tích vô hướng, bạn cần nắm vững các công thức và tính chất sau:
Để giúp bạn hiểu rõ hơn về cách giải bài tập, chúng tôi sẽ trình bày lời giải chi tiết cho từng câu hỏi trong bài 14:
(Nội dung câu a và lời giải chi tiết)
(Nội dung câu b và lời giải chi tiết)
(Nội dung câu c và lời giải chi tiết)
Ví dụ 1: Cho hai vectơ a = (1; 2) và b = (-3; 1). Tính tích vô hướng của a và b.
Giải:a.b = (1)(-3) + (2)(1) = -3 + 2 = -1
Ví dụ 2: Cho hai vectơ a = (2; -1) và b = (x; 3). Tìm giá trị của x để a và b vuông góc.
Giải: Để a và b vuông góc, ta cần có a.b = 0. Suy ra (2)(x) + (-1)(3) = 0, giải phương trình này ta được x = 3/2.
Để củng cố kiến thức, bạn có thể tự giải thêm các bài tập sau:
Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về cách giải bài 14 trang 96 SGK Toán 10 – Kết nối tri thức. Chúc bạn học tập tốt và đạt kết quả cao trong môn Toán!