Bài 6.7 trang 16 SGK Toán 10 Kết nối tri thức là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 6.7 trang 16 SGK Toán 10 Kết nối tri thức, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Vẽ các đường parabol sau:
Đề bài
Vẽ các đường parabol sau:
a) \(y = {x^2} - 3x + 2\)
b) \(y = - 2{x^2} + 2x + 3\)
c)\(y = {x^2} + 2x + 1\)
d)\(y = - {x^2} + x - 1\)
Phương pháp giải - Xem chi tiết
-Vẽ đồ thị \(y = a{x^2} + bx + c\left( {a \ne 0} \right)\)
Là 1 parabol có đỉnh là điểm \(I\left( { - \frac{b}{{2a}}; - \frac{\Delta }{{4a}}} \right)\), có trục đối xứng là đường thẳng \(x = - \frac{b}{{2a}}\)
Quay bề lõm lên trên nếu a>0, quay bề lõm xuống dưới nếu a<0
Xác định các điểm (đặc biệt) thuộc đồ thị.
Lời giải chi tiết
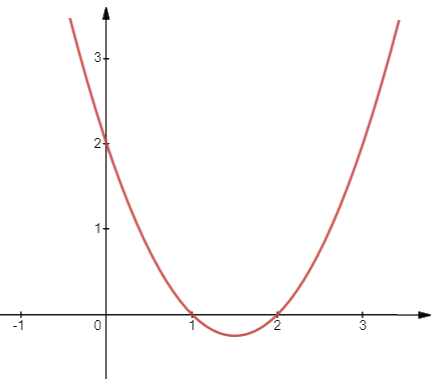
a) Đồ thị \(y = {x^2} - 3x + 2\)
- Có đỉnh là điểm \(I\left( {\frac{3}{2}; - \frac{1}{4}} \right)\), có trục đối xứng là đường thẳng \(x = \frac{3}{2}\)
- \(a = 1 > 0\), quay bề lõm lên trên
- Đi qua điểm (0;2);(1;0)
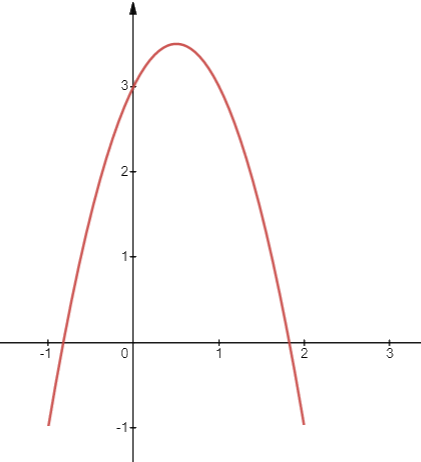
b) Đồ thị \(y = - 2{x^2} + 2x + 3\)
- Có đỉnh là điểm \(I\left( {\frac{1}{2};\frac{7}{2}} \right)\), có trục đối xứng là đường thẳng \(x = \frac{1}{2}\)
- \(a = - 2 < 0\), quay bề lõm xuống dưới
- Đi qua điểm (0;3);(1;3)
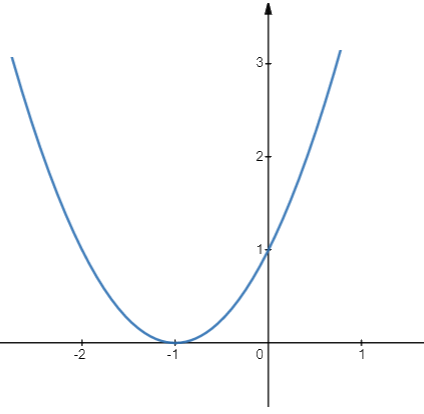
c) Đồ thị\(y = {x^2} + 2x + 1\)
- Có đỉnh là điểm \(I( - 1;0)\), có trục đối xứng là đường thẳng \(x = - 1\)
- \(a = 1 > 0\), quay bề lõm lên trên
- Đi qua điểm (0;1); (1;4)
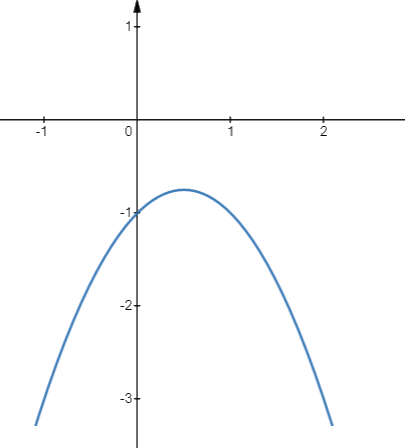
d) Đồ thị \(y = - {x^2} + x - 1\)
- Có đỉnh là điểm \(I\left( {\frac{1}{2};\frac{{ - 3}}{4}} \right)\), có trục đối xứng là đường thẳng \(x = \frac{1}{2}\)
- \(a = - 1 < 0\), quay bề lõm xuống dưới
- Đi qua điểm (0;-1);(1;-1)
Bài 6.7 trang 16 SGK Toán 10 – Kết nối tri thức là một bài toán ứng dụng thực tế về vectơ trong mặt phẳng. Để giải bài toán này, học sinh cần nắm vững các kiến thức cơ bản về vectơ, bao gồm:
Đề bài: Cho tam giác ABC. Gọi M là trung điểm của BC. Tìm vectơ AM theo hai vectơ AB và AC.
Lời giải:
Ta có:
Cụ thể:
Vì M là trung điểm của BC, ta có: BM = MC. Do đó, BC = 2BM.
Ta có thể biểu diễn vectơ AM như sau:
AM = AB + BM
Mà BM = (1/2)BC và BC = AC - AB. Vậy:
BM = (1/2)(AC - AB)
Thay vào biểu thức của AM, ta được:
AM = AB + (1/2)(AC - AB)
AM = AB + (1/2)AC - (1/2)AB
AM = (1/2)AB + (1/2)AC
Vậy, AM = (1/2)AB + (1/2)AC
Bài toán này là một ví dụ điển hình về việc sử dụng quy tắc trung điểm và quy tắc cộng vectơ để giải quyết các bài toán hình học. Việc hiểu rõ các quy tắc này sẽ giúp học sinh giải quyết nhiều bài toán tương tự một cách dễ dàng.
Ngoài ra, bài toán này còn có thể được mở rộng bằng cách thay đổi vị trí của điểm M trên cạnh BC. Ví dụ, nếu M là một điểm bất kỳ trên cạnh BC, ta có thể biểu diễn vectơ AM theo hai vectơ AB và AC bằng cách sử dụng hệ số tỉ lệ.
Để củng cố kiến thức về vectơ, học sinh có thể tự giải các bài tập tương tự sau:
Bài 6.7 trang 16 SGK Toán 10 – Kết nối tri thức là một bài tập quan trọng giúp học sinh hiểu rõ hơn về vectơ và các ứng dụng của nó trong hình học. Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trên đây, các em học sinh sẽ tự tin hơn khi giải bài tập và đạt kết quả tốt trong môn Toán.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Hãy truy cập website của chúng tôi để tìm hiểu thêm về các bài giải Toán 10 và các môn học khác.