Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10 tập 1 - Kết nối tri thức. Chúng tôi hiểu rằng việc tự học đôi khi gặp khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức.
Mục tiêu của chúng tôi là giúp bạn nắm vững kiến thức Toán học một cách nhanh chóng và hiệu quả nhất. Bài giải này sẽ cung cấp các bước giải chi tiết, rõ ràng, giúp bạn hiểu được bản chất của bài toán và cách áp dụng kiến thức vào thực tế.
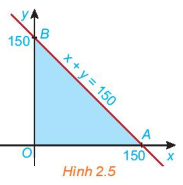
Cho đường thẳng d: x+y=150 trên mặt phẳng tọa độ Oxy. Đường thẳng này cắt hai trục tọa độ Ox và Oy tại hai điểm A và B. Biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn sau trên mặt phẳng tọa độ
Cho đường thẳng d: x+y=150 trên mặt phẳng tọa độ Oxy. Đường thẳng này cắt hai trục tọa độ Ox và Oy tại hai điểm A và B.
a) Xác định miền nghiệm \({D_1},{D_2},{D_3}\) của các bất phương trình tương ứng \(x \ge 0;y \ge 0\) và \(x + y \le 150\).
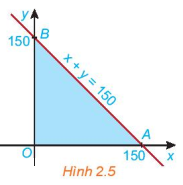
b) Miền tam giác OAB (H.2.5) có phải là giao điểm của các miền \({D_1},{D_2}\) và \({D_3}\) hay không?
c) Lấy một điểm trong tam giác OAB (chẳng hạn điểm (1;2)) hoặc một điểm trên cạnh nào đó của tam giác OAB (chẳng hạn điểm (1;149)) và kiểm tra xem tọa độ của các điểm đó có phải là nghiệm của hệ bất phương trình sau hay không:
\(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 150\end{array} \right.\)
Phương pháp giải:
a) Biểu diễn các miền nghiệm của từng bất phương trình \(x \ge 0;y \ge 0\) và \(x + y \le 150\)
Bước 1: Vẽ đường thẳng (nét liền) \(ax + by = c\).
Bước 2: Lấy điểm một điểm không thuộc đường thẳng \(ax + by = c\) và thay vào bất phương trình cần xác định miền nghiệm.
Bước 3: Nếu tọa độ điểm đó thỏa mãn bất phương trình thì miền nghiệm của bất phương trình chứa điểm đó.
b) Vẽ tất cả các miền miền \({D_1},{D_2}\) và \({D_3}\) lên cùng một mặt phẳng.
Lời giải chi tiết:
a)
Miền nghiệm của bất phương trình \(x \ge 0\)
Bước 1: Vẽ đường thẳng (nét liền) \(x = 0\). Đây là trục Oy.
Bước 2: Lấy điểm A(150;0) không thuộc trục Oy và thay vào biểu thức \(x\), ta được: \(x = 150 \ge 0\).
Bước 3: Do điểm A thỏa mãn bất phương trình nên miền nghiệm của bất phương trình là nửa mặt phẳng có chứa điểm A.
Minh họa (phần không bị gạch chéo):
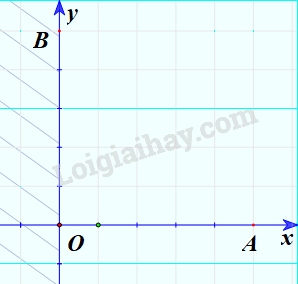
Miền nghiệm của bất phương trình \(y \ge 0\)
Bước 1: Vẽ đường thẳng (nét liền) \(y = 0\). Đây là trục Ox.
Bước 2: Lấy điểm B(0;150) không thuộc trục Ox và thay vào biểu thức \(y\), ta được: \(y = 150 \ge 0\).
Bước 3: Do điểm B thỏa mãn bất phương trình nên miền nghiệm của bất phương trình là nửa mặt phẳng có chứa điểm B.
Minh họa (phần không bị gạch chéo):
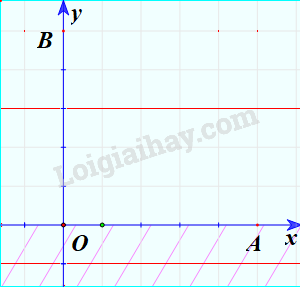
Miền nghiệm của bất phương trình \(x + y \le 150\):
Bước 1: Vẽ đường thẳng (nét liền) \(x + y = 150\).
Bước 2: Lấy điểm O(0;0) không thuộc đường thẳng \(x + y = 150\) và thay vào \(x + y\), ta được: \(0 + 0 = 0 \le 150\)
Bước 3: Do điểm O thỏa mãn bất phương trình nên miền nghiệm của bất phương trình là nửa mặt phẳng có chứa điểm O.
Minh họa (phần không bị gạch chéo):
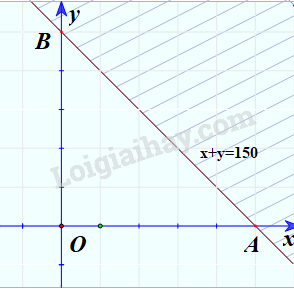
Vậy \({D_1}\) là nửa trên mặt phẳng có bờ là trục Oy, \({D_2}\) là nửa bên phải mặt phẳng có bờ là trục Ox và \({D_3}\) là nửa mặt phẳng có bờ là đường thẳng x+y=150 chứa điểm O.
b) Vẽ tất cả các miền miền \({D_1},{D_2}\) và \({D_3}\) lên cùng một mặt phẳng.
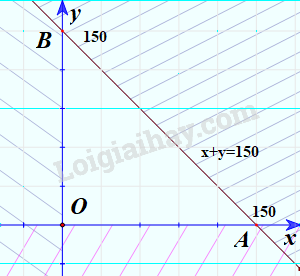
=>Miền tam giác OAB (H.2.5) có phải là giao điểm của các miền \({D_1},{D_2}\) và \({D_3}\)
c) Lấy một điểm trong tam giác OAB (chẳng hạn điểm (1;2)) hoặc một điểm trên cạnh nào đó của tam giác OAB (chẳng hạn điểm (1;149)) và kiểm tra xem tọa độ của các điểm đó có phải là nghiệm của hệ bất phương trình sau hay không:
\(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 150\end{array} \right.\)
Lấy điểm (1;2) trong tam giác OAB, thay vào hệ \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 150\end{array} \right.\)
Ta được:
\(\left\{ {\begin{array}{*{20}{l}}{1 \ge 0}\\{2 \ge 0}\\{1 + 2 \le 150}\end{array}} \right.\) (luôn đúng)
Vậy điểm (1;2) là nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 150\end{array} \right.\)
Lấy điểm (1;149), thay vào hệ \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 150\end{array} \right.\)
Ta được:
\(\left\{ {\begin{array}{*{20}{l}}{1 \ge 0}\\{149 \ge 0}\\{1 + 149 \le 150}\end{array}} \right.\) (luôn đúng)
Vậy điểm (1;149) là nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 150\end{array} \right.\)
Biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn sau trên mặt phẳng tọa độ: \(\left\{ \begin{array}{l}x \ge 0\\y > 0\\x + y \le 100\\2x + y < 120\end{array} \right.\)
Phương pháp giải:
Bước 1: Xác định miền nghiệm của bất phương trình \(x \ge 0\)
Bước 2: Xác định miền nghiệm của bất phương trình \(y > 0\)
Bước 3: Xác định miền nghiệm của bất phương trình \(x + y \le 100\)
Bước 4: Xác định miền nghiệm của bất phương trình \(2x + y < 120\)
Miền không bị gạch là miền nghiệm của hệ bất phương trình đã cho.
Lời giải chi tiết:
Bước 1: Xác định miền nghiệm của bất phương trình \(x \ge 0\)
Miền nghiệm của bất phương trình \(x \ge 0\) là nửa mặt phẳng bờ Oy chứa điểm (1;0).
Bước 2: Xác định miền nghiệm của bất phương trình \(y > 0\)
Miền nghiệm của bất phương trình \(y > 0\) là nửa mặt phẳng bờ Ox chứa điểm (0;1) không kể trục Ox.
Bước 3: Xác định miền nghiệm của bất phương trình \(x + y \le 100\)
+ Vẽ đường thẳng d: x+y=100
+ Vì 0+0=0
Do đó, miền nghiệm của bất phương trình \(x + y \le 100\) là nửa mặt phẳng bờ d chứa gốc tọa độ O.
Bước 4: Xác định miền nghiệm của bất phương trình \(2x + y < 120\)
Tương tự miền nghiệm của bất phương trình \(2x + y < 120\) là nửa mặt phẳng bờ d’ chúa gốc tọa độ O. (không kể đường thẳng d’).
Khi đó miền không bị gạch là giao của các miền nghiệm của các bất phương trình trong hệ. Vậy miền không bị gạch là miền nghiệm của hệ bất phương trình đã cho (Không kể đoạn thẳng OC và CD).
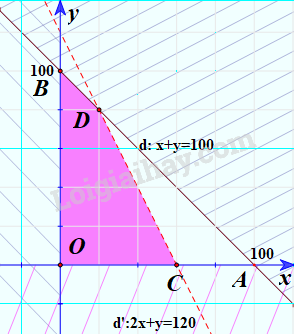
Cho đường thẳng d: x+y=150 trên mặt phẳng tọa độ Oxy. Đường thẳng này cắt hai trục tọa độ Ox và Oy tại hai điểm A và B.
a) Xác định miền nghiệm \({D_1},{D_2},{D_3}\) của các bất phương trình tương ứng \(x \ge 0;y \ge 0\) và \(x + y \le 150\).
b) Miền tam giác OAB (H.2.5) có phải là giao điểm của các miền \({D_1},{D_2}\) và \({D_3}\) hay không?
c) Lấy một điểm trong tam giác OAB (chẳng hạn điểm (1;2)) hoặc một điểm trên cạnh nào đó của tam giác OAB (chẳng hạn điểm (1;149)) và kiểm tra xem tọa độ của các điểm đó có phải là nghiệm của hệ bất phương trình sau hay không:
\(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 150\end{array} \right.\)
Phương pháp giải:
a) Biểu diễn các miền nghiệm của từng bất phương trình \(x \ge 0;y \ge 0\) và \(x + y \le 150\)
Bước 1: Vẽ đường thẳng (nét liền) \(ax + by = c\).
Bước 2: Lấy điểm một điểm không thuộc đường thẳng \(ax + by = c\) và thay vào bất phương trình cần xác định miền nghiệm.
Bước 3: Nếu tọa độ điểm đó thỏa mãn bất phương trình thì miền nghiệm của bất phương trình chứa điểm đó.
b) Vẽ tất cả các miền miền \({D_1},{D_2}\) và \({D_3}\) lên cùng một mặt phẳng.
Lời giải chi tiết:
a)
Miền nghiệm của bất phương trình \(x \ge 0\)
Bước 1: Vẽ đường thẳng (nét liền) \(x = 0\). Đây là trục Oy.
Bước 2: Lấy điểm A(150;0) không thuộc trục Oy và thay vào biểu thức \(x\), ta được: \(x = 150 \ge 0\).
Bước 3: Do điểm A thỏa mãn bất phương trình nên miền nghiệm của bất phương trình là nửa mặt phẳng có chứa điểm A.
Minh họa (phần không bị gạch chéo):
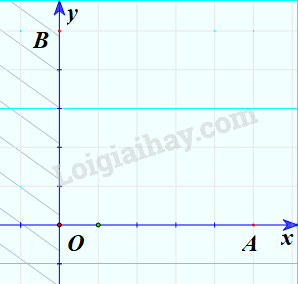
Miền nghiệm của bất phương trình \(y \ge 0\)
Bước 1: Vẽ đường thẳng (nét liền) \(y = 0\). Đây là trục Ox.
Bước 2: Lấy điểm B(0;150) không thuộc trục Ox và thay vào biểu thức \(y\), ta được: \(y = 150 \ge 0\).
Bước 3: Do điểm B thỏa mãn bất phương trình nên miền nghiệm của bất phương trình là nửa mặt phẳng có chứa điểm B.
Minh họa (phần không bị gạch chéo):
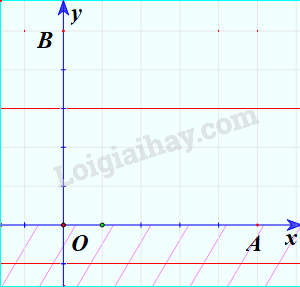
Miền nghiệm của bất phương trình \(x + y \le 150\):
Bước 1: Vẽ đường thẳng (nét liền) \(x + y = 150\).
Bước 2: Lấy điểm O(0;0) không thuộc đường thẳng \(x + y = 150\) và thay vào \(x + y\), ta được: \(0 + 0 = 0 \le 150\)
Bước 3: Do điểm O thỏa mãn bất phương trình nên miền nghiệm của bất phương trình là nửa mặt phẳng có chứa điểm O.
Minh họa (phần không bị gạch chéo):
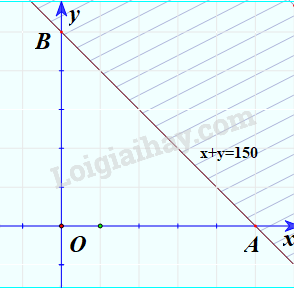
Vậy \({D_1}\) là nửa trên mặt phẳng có bờ là trục Oy, \({D_2}\) là nửa bên phải mặt phẳng có bờ là trục Ox và \({D_3}\) là nửa mặt phẳng có bờ là đường thẳng x+y=150 chứa điểm O.
b) Vẽ tất cả các miền miền \({D_1},{D_2}\) và \({D_3}\) lên cùng một mặt phẳng.
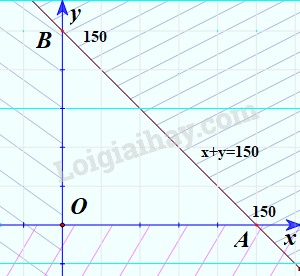
=>Miền tam giác OAB (H.2.5) có phải là giao điểm của các miền \({D_1},{D_2}\) và \({D_3}\)
c) Lấy một điểm trong tam giác OAB (chẳng hạn điểm (1;2)) hoặc một điểm trên cạnh nào đó của tam giác OAB (chẳng hạn điểm (1;149)) và kiểm tra xem tọa độ của các điểm đó có phải là nghiệm của hệ bất phương trình sau hay không:
\(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 150\end{array} \right.\)
Lấy điểm (1;2) trong tam giác OAB, thay vào hệ \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 150\end{array} \right.\)
Ta được:
\(\left\{ {\begin{array}{*{20}{l}}{1 \ge 0}\\{2 \ge 0}\\{1 + 2 \le 150}\end{array}} \right.\) (luôn đúng)
Vậy điểm (1;2) là nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 150\end{array} \right.\)
Lấy điểm (1;149), thay vào hệ \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 150\end{array} \right.\)
Ta được:
\(\left\{ {\begin{array}{*{20}{l}}{1 \ge 0}\\{149 \ge 0}\\{1 + 149 \le 150}\end{array}} \right.\) (luôn đúng)
Vậy điểm (1;149) là nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 150\end{array} \right.\)
Biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn sau trên mặt phẳng tọa độ: \(\left\{ \begin{array}{l}x \ge 0\\y > 0\\x + y \le 100\\2x + y < 120\end{array} \right.\)
Phương pháp giải:
Bước 1: Xác định miền nghiệm của bất phương trình \(x \ge 0\)
Bước 2: Xác định miền nghiệm của bất phương trình \(y > 0\)
Bước 3: Xác định miền nghiệm của bất phương trình \(x + y \le 100\)
Bước 4: Xác định miền nghiệm của bất phương trình \(2x + y < 120\)
Miền không bị gạch là miền nghiệm của hệ bất phương trình đã cho.
Lời giải chi tiết:
Bước 1: Xác định miền nghiệm của bất phương trình \(x \ge 0\)
Miền nghiệm của bất phương trình \(x \ge 0\) là nửa mặt phẳng bờ Oy chứa điểm (1;0).
Bước 2: Xác định miền nghiệm của bất phương trình \(y > 0\)
Miền nghiệm của bất phương trình \(y > 0\) là nửa mặt phẳng bờ Ox chứa điểm (0;1) không kể trục Ox.
Bước 3: Xác định miền nghiệm của bất phương trình \(x + y \le 100\)
+ Vẽ đường thẳng d: x+y=100
+ Vì 0+0=0
Do đó, miền nghiệm của bất phương trình \(x + y \le 100\) là nửa mặt phẳng bờ d chứa gốc tọa độ O.
Bước 4: Xác định miền nghiệm của bất phương trình \(2x + y < 120\)
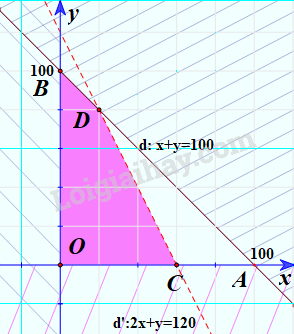
Tương tự miền nghiệm của bất phương trình \(2x + y < 120\) là nửa mặt phẳng bờ d’ chúa gốc tọa độ O. (không kể đường thẳng d’).
Khi đó miền không bị gạch là giao của các miền nghiệm của các bất phương trình trong hệ. Vậy miền không bị gạch là miền nghiệm của hệ bất phương trình đã cho (Không kể đoạn thẳng OC và CD).
Mục 2 của chương trình Toán 10 tập 1 - Kết nối tri thức tập trung vào các khái niệm cơ bản về tập hợp, các phép toán trên tập hợp và các tính chất của chúng. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương trình Toán học ở các lớp trên. Bài tập trang 28 và 29 SGK Toán 10 tập 1 yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán cụ thể, từ đó củng cố và nâng cao hiểu biết về tập hợp.
Bài tập này yêu cầu học sinh xác định các phần tử thuộc một tập hợp cho trước, dựa trên một điều kiện hoặc tiêu chí nhất định. Để giải bài tập này, học sinh cần hiểu rõ khái niệm về tập hợp và cách xác định các phần tử của tập hợp.
Bài tập này yêu cầu học sinh xác định các tập hợp con của một tập hợp cho trước. Để giải bài tập này, học sinh cần hiểu rõ khái niệm về tập hợp con và cách xác định các tập hợp con.
Bài tập này yêu cầu học sinh thực hiện các phép toán trên tập hợp, như hợp, giao, hiệu và phần bù. Để giải bài tập này, học sinh cần hiểu rõ các định nghĩa và tính chất của các phép toán trên tập hợp.
| Phép toán | Ký hiệu | Định nghĩa |
|---|---|---|
| Hợp | A ∪ B | Tập hợp chứa tất cả các phần tử thuộc A hoặc B (hoặc cả hai). |
| Giao | A ∩ B | Tập hợp chứa tất cả các phần tử thuộc cả A và B. |
| Hiệu | A \ B | Tập hợp chứa tất cả các phần tử thuộc A nhưng không thuộc B. |
| Phần bù | CA | Tập hợp chứa tất cả các phần tử không thuộc A. |
Để giải tốt các bài tập về tập hợp, bạn nên:
Việc giải các bài tập trong mục 2 trang 28, 29 SGK Toán 10 tập 1 - Kết nối tri thức là một bước quan trọng trong quá trình học Toán 10. Hy vọng rằng với những hướng dẫn chi tiết và lời khuyên trên, bạn sẽ tự tin hơn khi giải quyết các bài tập về tập hợp và đạt được kết quả tốt nhất. Chúc bạn học tập hiệu quả!