Giaitoan.edu.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 2 trang 15, 16 sách giáo khoa Toán 10 tập 1 chương trình Kết nối tri thức. Bài viết này sẽ giúp các em học sinh nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi cung cấp đáp án đầy đủ, kèm theo các bước giải thích rõ ràng, giúp các em dễ dàng theo dõi và áp dụng vào các bài tập tương tự.
Các mệnh đề sau đúng hay sai? a) Mọi số nguyên đều viết được dưới dạng phân số Cho tập hợp C = {-4; 0; 1; 2}. Các mệnh đề sau đúng hay sai? Cho hai tập hợp C = và D =. Các mệnh đề sau đúng hay sai? Hãy ghép mỗi dòng ở cột bên trái với một dòng thích hợp ở cột bên phải.
Các mệnh đề sau đúng hay sai?
a) Mọi số nguyên đều viết được dưới dạng phân số
b) Tập hợp các số thực chứa tập hợp các số hữu tỉ;
c) Tồn tại một số thực không là số hữu tỉ.
Phương pháp giải:
Nhắc lại: \(\mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R}\)
Lời giải chi tiết:
a) Mệnh đề “Mọi số nguyên đều viết được dưới dạng phân số” đúng.
Vì \(\forall a \in \mathbb{Z}:a = \dfrac{a}{1}\)
Hoặc: \(a \in \mathbb{Z} \subset \mathbb{Q}\) => mỗi số nguyên cũng là một phân số.
b) Mệnh đề "Tập hợp các số thực chứa tập hợp các số hữu tỉ" là mệnh đề đúng.
c) Mệnh đề “Tồn tại một số thực không là số hữu tỉ” đúng.
Ví dụ: \(\sqrt 2 \) ( vì \(\sqrt 2 \in \mathbb{R};\;\sqrt 2 \notin \mathbb{Q}\)).
Cho hai tập hợp C = {\(x \in \mathbb{R}|x \ge 3\)} và D = {\(x \in \mathbb{R}|x\;\, > 3\)}. Các mệnh đề sau đúng hay sai?
a) C, D là các tập con của \(\mathbb{R}\);
b) \(\forall x,\;x \in C \Rightarrow x \in D\);
c) \(3 \in C\) nhưng \(3 \notin D\);
d) \(C = D\)
Phương pháp giải:
+) \(C \subset \mathbb{R}\) nếu mọi phần tử của C đều là phần tử của \(\mathbb{R}\).
+) \(C = D \Leftrightarrow \left\{ \begin{array}{l}C \subset D\\C \supset D\end{array} \right.\)
Lời giải chi tiết:
a) Hiển nhiên: C, D là các tập con của \(\mathbb{R}\).
Vậy mệnh đề này đúng.
b) Mệnh đề “\(\forall x,\;x \in C \Rightarrow x \in D\)” sai. Vì \(3 \in C\) nhưng \(3 \notin D\);
c) Mệnh đề “\(3 \in C\) nhưng \(3 \notin D\)” đúng;
d) Mệnh đề “\(C = D\)” sai vì \(3 \in C\) nhưng \(3 \notin D\).
Cho tập hợp C = {-4; 0; 1; 2}. Các mệnh đề sau đúng hay sai?
a) C là tập con của \(\mathbb{Z}\)
b) C là tập con của \(\mathbb{N}\)
c) C là tập con của \(\mathbb{R}\)
Phương pháp giải:
C là tập con của X nếu mỗi phần tử của C đều là phần tử của X.
Lời giải chi tiết:
a) Dễ thấy: \( - 4;{\rm{ }}0;{\rm{ }}1;{\rm{ }}2 \in \mathbb{Z}\)
Vậy C là tập con của \(\mathbb{Z}\), mệnh đề đúng.
b) Vì \( - 4 \notin \mathbb{N}\) nên C không là tập con của \(\mathbb{N}\)
Vậy mệnh đề sai.
c) Dễ thấy: \( - 4;{\rm{ }}0;{\rm{ }}1;{\rm{ }}2 \in \mathbb{R}\)
Vậy C là tập con của \(\mathbb{R}\), mệnh đề đúng.
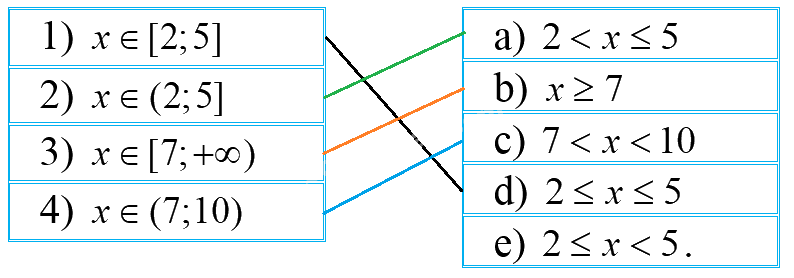
Hãy ghép mỗi dòng ở cột bên trái với một dòng thích hợp ở cột bên phải.
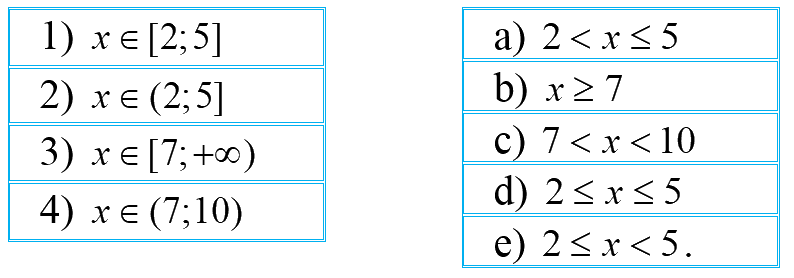
Lời giải chi tiết:
1) \(x \in [2;5] \Leftrightarrow 2 \le x \le 5\). Nối 1) với d)
2) \(x \in (2;5] \Leftrightarrow 2 < x \le 5\). Nối 2) với a)
3) \(x \in [7; + \infty ) \Leftrightarrow x \ge 7\). Nối 3) với b)
4) \(x \in (7;10) \Leftrightarrow 7 < x < 10\). Nối 4) với c)
Các mệnh đề sau đúng hay sai?
a) Mọi số nguyên đều viết được dưới dạng phân số
b) Tập hợp các số thực chứa tập hợp các số hữu tỉ;
c) Tồn tại một số thực không là số hữu tỉ.
Phương pháp giải:
Nhắc lại: \(\mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R}\)
Lời giải chi tiết:
a) Mệnh đề “Mọi số nguyên đều viết được dưới dạng phân số” đúng.
Vì \(\forall a \in \mathbb{Z}:a = \dfrac{a}{1}\)
Hoặc: \(a \in \mathbb{Z} \subset \mathbb{Q}\) => mỗi số nguyên cũng là một phân số.
b) Mệnh đề "Tập hợp các số thực chứa tập hợp các số hữu tỉ" là mệnh đề đúng.
c) Mệnh đề “Tồn tại một số thực không là số hữu tỉ” đúng.
Ví dụ: \(\sqrt 2 \) ( vì \(\sqrt 2 \in \mathbb{R};\;\sqrt 2 \notin \mathbb{Q}\)).
Cho tập hợp C = {-4; 0; 1; 2}. Các mệnh đề sau đúng hay sai?
a) C là tập con của \(\mathbb{Z}\)
b) C là tập con của \(\mathbb{N}\)
c) C là tập con của \(\mathbb{R}\)
Phương pháp giải:
C là tập con của X nếu mỗi phần tử của C đều là phần tử của X.
Lời giải chi tiết:
a) Dễ thấy: \( - 4;{\rm{ }}0;{\rm{ }}1;{\rm{ }}2 \in \mathbb{Z}\)
Vậy C là tập con của \(\mathbb{Z}\), mệnh đề đúng.
b) Vì \( - 4 \notin \mathbb{N}\) nên C không là tập con của \(\mathbb{N}\)
Vậy mệnh đề sai.
c) Dễ thấy: \( - 4;{\rm{ }}0;{\rm{ }}1;{\rm{ }}2 \in \mathbb{R}\)
Vậy C là tập con của \(\mathbb{R}\), mệnh đề đúng.
Cho hai tập hợp C = {\(x \in \mathbb{R}|x \ge 3\)} và D = {\(x \in \mathbb{R}|x\;\, > 3\)}. Các mệnh đề sau đúng hay sai?
a) C, D là các tập con của \(\mathbb{R}\);
b) \(\forall x,\;x \in C \Rightarrow x \in D\);
c) \(3 \in C\) nhưng \(3 \notin D\);
d) \(C = D\)
Phương pháp giải:
+) \(C \subset \mathbb{R}\) nếu mọi phần tử của C đều là phần tử của \(\mathbb{R}\).
+) \(C = D \Leftrightarrow \left\{ \begin{array}{l}C \subset D\\C \supset D\end{array} \right.\)
Lời giải chi tiết:
a) Hiển nhiên: C, D là các tập con của \(\mathbb{R}\).
Vậy mệnh đề này đúng.
b) Mệnh đề “\(\forall x,\;x \in C \Rightarrow x \in D\)” sai. Vì \(3 \in C\) nhưng \(3 \notin D\);
c) Mệnh đề “\(3 \in C\) nhưng \(3 \notin D\)” đúng;
d) Mệnh đề “\(C = D\)” sai vì \(3 \in C\) nhưng \(3 \notin D\).
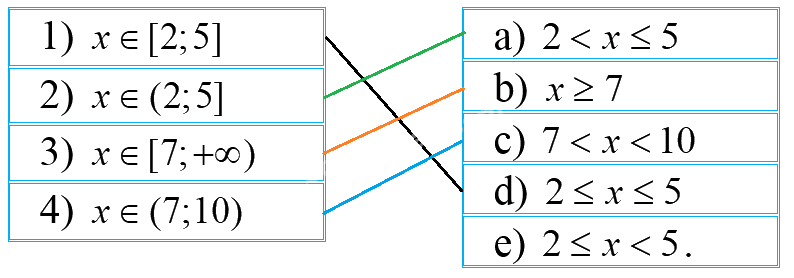
Hãy ghép mỗi dòng ở cột bên trái với một dòng thích hợp ở cột bên phải.
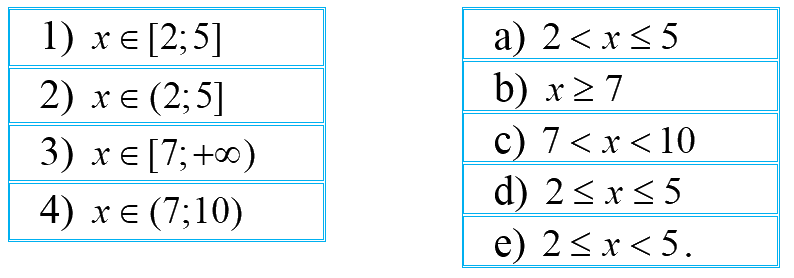
Lời giải chi tiết:
1) \(x \in [2;5] \Leftrightarrow 2 \le x \le 5\). Nối 1) với d)
2) \(x \in (2;5] \Leftrightarrow 2 < x \le 5\). Nối 2) với a)
3) \(x \in [7; + \infty ) \Leftrightarrow x \ge 7\). Nối 3) với b)
4) \(x \in (7;10) \Leftrightarrow 7 < x < 10\). Nối 4) với c)
Mục 2 của chương trình Toán 10 tập 1 Kết nối tri thức tập trung vào các khái niệm cơ bản về tập hợp số, bao gồm tập số thực, các phép toán trên tập số thực và các tính chất của chúng. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo.
Mục 2 bao gồm các nội dung chính sau:
Dưới đây là lời giải chi tiết cho các bài tập trong mục 2 trang 15, 16 SGK Toán 10 tập 1 Kết nối tri thức:
(Đề bài)
Lời giải:
...
(Đề bài)
Lời giải:
...
(Đề bài)
Lời giải:
...
Để giúp các em hiểu rõ hơn về các khái niệm và phương pháp giải, chúng tôi cung cấp một số ví dụ minh họa và bài tập luyện tập:
(Đề bài)
Lời giải:
...
(Đề bài)
Đáp án:
...
Khi giải các bài tập về tập số thực, các em cần lưu ý:
Kiến thức về tập số thực có ứng dụng rộng rãi trong nhiều lĩnh vực của toán học và khoa học tự nhiên, như giải phương trình, bất phương trình, tính giới hạn, đạo hàm, tích phân, vật lý, hóa học, kinh tế,...
Hy vọng rằng với lời giải chi tiết và các ví dụ minh họa trên, các em học sinh đã nắm vững kiến thức về mục 2 trang 15, 16 SGK Toán 10 tập 1 Kết nối tri thức. Chúc các em học tập tốt!
| Công thức | Mô tả |
|---|---|
| |a| | Giá trị tuyệt đối của a |
| a < b | a nhỏ hơn b |
| a > b | a lớn hơn b |