Bài 1.23 trang 20 SGK Toán 10 tập 1 – Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 10. Bài tập này yêu cầu học sinh vận dụng kiến thức về tập hợp, các phép toán trên tập hợp để giải quyết các bài toán cụ thể.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 1.23 trang 20 SGK Toán 10 tập 1 – Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Phần không bị gạch trên trục số dưới đây biểu diễn tập hợp số nào?
Đề bài
Phần không bị gạch trên trục số dưới đây biểu diễn tập hợp số nào?

Lời giải chi tiết
Ta có:
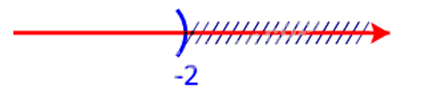
Biểu diễn khoảng \(\left( { - \infty ; - 2} \right)\)
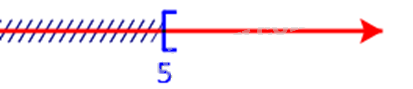
Biểu diễn nửa khoảng \([5; + \infty )\)
Vậy phần không bị gạch trên trục số là \(\left( { - \infty ; - 2} \right) \cup [5; + \infty )\)
Cách 2:
Dễ thấy phần bị gạch trên trục số là nửa khoảng \([-2;5)\)

Vậy phần không bị gạch trên trục số là \(\left( { - \infty ; - 2} \right) \cup [5; + \infty )\)
Bài 1.23 SGK Toán 10 tập 1 – Kết nối tri thức yêu cầu chúng ta thực hiện các phép toán trên tập hợp, bao gồm hợp, giao, hiệu và phần bù của tập hợp. Để giải bài tập này một cách hiệu quả, trước hết chúng ta cần nắm vững định nghĩa và các tính chất cơ bản của các phép toán này.
Bài 1.23 thường đưa ra các tập hợp cụ thể và yêu cầu chúng ta thực hiện các phép toán trên chúng. Ví dụ, cho A = {1, 2, 3} và B = {2, 4, 5}, hãy tìm A ∪ B, A ∩ B, A \ B và B \ A.
Giả sử bài toán yêu cầu:
Cho A = {1, 2, 3, 4, 5} và B = {3, 5, 6, 7}. Hãy tính:
Lời giải:
Để hiểu sâu hơn về các phép toán trên tập hợp, bạn có thể thực hành với các bài tập tương tự. Hãy thử thay đổi các tập hợp A và B và tính toán lại các phép toán. Điều này sẽ giúp bạn làm quen với các khái niệm và rèn luyện kỹ năng giải toán.
Tập hợp có rất nhiều ứng dụng trong thực tế, ví dụ như:
Bài 1.23 trang 20 SGK Toán 10 tập 1 – Kết nối tri thức là một bài tập cơ bản nhưng quan trọng trong chương trình học Toán 10. Việc nắm vững lý thuyết và thực hành giải các bài tập tương tự sẽ giúp bạn tự tin hơn trong việc học tập và giải quyết các vấn đề liên quan đến tập hợp.