Bài 3.15 trang 44 SGK Toán 10 tập 1 thuộc chương 3: Hàm số và đồ thị. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai, điều kiện xác định và tập giá trị của hàm số để giải quyết.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho tam giác ABC có B = 60, C = 45,AC = 10. Tính a,R,S,r.
Đề bài
Cho tam giác ABC có \(\widehat B = {60^o},\;\,\widehat C = {45^o},AC = 10\). Tính \(a,R,S,r\).
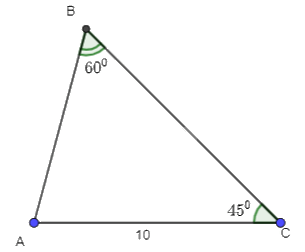
Phương pháp giải - Xem chi tiết
Định lí sin: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\)
Lời giải chi tiết
Theo định lí sin: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\quad (*)\)
+) Ta có: \(\hat A = {180^o} - \left( {\hat B + \;\hat C} \right) = {180^o} - \left( {{{60}^o} + {{45}^o}} \right) = {75^o}\)
\( \Rightarrow a = \frac{b}{{\sin B}}.\sin A = \frac{{10}}{{\sin {{60}^o}}}.\sin {75^o} \approx 11,154\)
+) \((*) \Rightarrow R = \frac{b}{{2\sin B}} = \frac{{10}}{{2\sin {{60}^o}}} = \frac{{10}}{{2.\frac{{\sqrt 3 }}{2}}} = \frac{{10\sqrt 3 }}{3}.\)
+) Diện tích tam giác ABC là: \(S = \frac{1}{2}ab.\sin {\mkern 1mu} \hat C\) \( \approx \frac{1}{2}.11,154.10.\sin {45^o}\)\( \approx 39,44\)
+) Lại có: \(R = \frac{c}{{2\sin C}}\)\( \Rightarrow c = 2.\frac{{10\sqrt 3 }}{3}.\sin {45^o} = \frac{{10\sqrt 6 }}{3} \approx 8,165\)
\( \Rightarrow p = \frac{{a + b + c}}{2} \approx \frac{{11,154 + 10 + 8,165}}{2} \approx 14,66\)
\( \Rightarrow r = \frac{S}{p} \approx \frac{{39,44}}{{14,66}} \approx 2,7\)
Bài 3.15 SGK Toán 10 tập 1 – Kết nối tri thức yêu cầu chúng ta xét hàm số f(x) = x2 - 4x + 3 và thực hiện các yêu cầu sau:
1. Tập xác định của hàm số:
Hàm số f(x) = x2 - 4x + 3 là một hàm số bậc hai. Hàm số bậc hai có tập xác định là tập số thực, tức là D = ℝ.
2. Tìm các giá trị của x sao cho f(x) = 0:
Để tìm các giá trị của x sao cho f(x) = 0, ta giải phương trình:
x2 - 4x + 3 = 0
Phương trình này có thể được giải bằng cách phân tích thành nhân tử:
(x - 1)(x - 3) = 0
Vậy, x = 1 hoặc x = 3.
3. Tìm các giá trị của x sao cho f(x) = 3:
Để tìm các giá trị của x sao cho f(x) = 3, ta giải phương trình:
x2 - 4x + 3 = 3
x2 - 4x = 0
x(x - 4) = 0
Vậy, x = 0 hoặc x = 4.
4. Tìm các giá trị của x sao cho f(x) > 0:
Để tìm các giá trị của x sao cho f(x) > 0, ta xét dấu của biểu thức (x - 1)(x - 3):
Vậy, f(x) > 0 khi x < 1 hoặc x > 3.
5. Tìm các giá trị của x sao cho f(x) ≤ 0:
Để tìm các giá trị của x sao cho f(x) ≤ 0, ta xét dấu của biểu thức (x - 1)(x - 3):
f(x) ≤ 0 khi 1 ≤ x ≤ 3.
Thông qua việc giải bài 3.15 trang 44 SGK Toán 10 tập 1 – Kết nối tri thức, chúng ta đã củng cố kiến thức về hàm số bậc hai, tập xác định, nghiệm của hàm số và cách xét dấu của biểu thức bậc hai. Bài tập này là nền tảng quan trọng để học tốt các bài toán về hàm số trong chương trình Toán 10.
Để luyện tập thêm, các em có thể tham khảo các bài tập sau:
Hy vọng với lời giải chi tiết này, các em học sinh sẽ hiểu rõ hơn về bài 3.15 trang 44 SGK Toán 10 tập 1 – Kết nối tri thức và tự tin hơn trong việc giải các bài tập tương tự.