Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập Toán 10 tập 2 Kết nối tri thức. Chúng tôi hiểu rằng việc tự học đôi khi gặp nhiều khó khăn, vì vậy chúng tôi luôn cố gắng mang đến những giải pháp tốt nhất để giúp bạn nắm vững kiến thức.
Mục 1 của chương trình Toán 10 tập 2 tập trung vào các khái niệm quan trọng về hàm số bậc hai. Việc hiểu rõ các khái niệm này là nền tảng để giải quyết các bài toán phức tạp hơn trong tương lai.
Hãy chỉ ra một đặc điểm chung của các biểu thức dưới đây: Hãy cho biết biểu thức nào sau đây là tam thức bậc hai. c) Nhận xét về dấu của f(x) và dấu của hệ số a trên từng khoảng đó. Nêu nội dung thay vào các ô có dấu “?” trong bảng sau cho thích hợp
Hãy chỉ ra một đặc điểm chung của các biểu thức dưới đây:
\(A = 0,5{x^2}\)
\(B = 1 - {x^2}\)
\(C = {x^2} + x + 1\)
\(D = (1 - x)(2x + 1)\)
Lời giải chi tiết:
Ta có :
\(A = 0,5{x^2}\)
\(B = 1 - {x^2}\)
\(C = {x^2} + x + 1\)
\(D = (1 - x)(2x + 1) = 2x + 1 - 2{x^2} - x = - 2{x^2} + x + 1\)
=> Các biểu thức đều có dạng \(a{x^2} + bx + c(a \ne 0)\), a,b,c là các số thực.
Hãy cho biết biểu thức nào sau đây là tam thức bậc hai.
\(A = 3x + 2\sqrt x + 1\)
\(B = - 5{x^4} - 3{x^2} + 4\)
\(C = - \frac{2}{3}{x^2} + 7x - 4\)
\(D = {\left( {\frac{1}{x}} \right)^2} + 2.\frac{1}{x} + 3\)
Phương pháp giải:
Tam thức bậc hai là biểu thức có dạng \(a{x^2} + bx + c\), trong đó a,b,c là những số cho trước \(\left( {a \ne 0} \right)\)
Lời giải chi tiết:
Biểu thức \(C = - \frac{2}{3}{x^2} + 7x - 4\) là tam thức bậc hai
Biểu thức A không là tam thức bậc hai vì chứa \(\sqrt x \)
Biểu thức B không là tam thức bậc hai vì chứa \({x^4}\)
Biểu thức D không là tam thức bậc hai vì chứa \({\left( {\frac{1}{x}} \right)^2}\)
Cho hàm số bậc hai \(y = f(x) = {x^2} - 4x + 3\)
a) Xác định hệ số a. Tính \(f(0);f(1);f(2);f(3);f(4)\) và nhận xét về dấu của chúng so với dấu của hệ số a
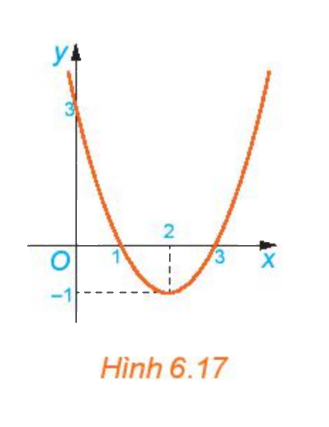
b) Cho đồ thị hàm số y=f(x) (H.6.17). Xét từng khoảng \(\left( { - \infty ;1} \right);\left( {1;3} \right);\left( {3; + \infty } \right)\), đồ thị nằm phía trên hay phía dưới trục Ox?
c) Nhận xét về dấu của f(x) và dấu của hệ số a trên từng khoảng đó.
Lời giải chi tiết:
a) Hệ số a là: a=1
\(f(0) = {0^2} - 4.0 + 3 = 3\)
\(f(1) = {1^2} - 4.1 + 3 = 0\)
\(f(2) = {2^2} - 4.2 + 3 = - 1\)
\(f(3) = {3^2} - 4.3 + 3 = 0\)
\(f(4) = {4^2} - 4.4 + 3 = 3\)
=> f(0); f(4) cùng dấu với hệ số a; f(2) khác dấu với hệ số a
b) Nhìn vào đồ thị ta thấy
- Trên khoảng \(\left( { - \infty ;1} \right)\) đồ thị nằm phía trên trục hoành
- Trên khoảng \(\left( {1;3} \right)\), đồ thị nằm phía dưới trục hoành
- Trên khoảng \(\left( {3; + \infty } \right)\), đồ thị nằm phía trên trục hoành
c) - Trên khoảng \(\left( { - \infty ;1} \right)\) đồ thị nằm phía trên trục hoành => f(x)>0, cùng dầu với hệ số a
- Trên khoảng \(\left( {1;3} \right)\), đồ thị nằm phía dưới trục hoành => f(x) <0, khác dấu với hệ số a
- Trên khoảng \(\left( {3; + \infty } \right)\), đồ thị nằm phía trên trục hoành => f(x)>0, cùng dấu với hệ số a
Xét dấu các tam thức bậc hai sau:
a) \( - 3{x^2} + x - \sqrt 2 \)
b) \({x^2} + 8x + 16\)
c) \( - 2{x^2} + 7x - 3\)
Phương pháp giải:
Xét dấu tam thức bậc hai \(f(x) = a{x^2} + bx + c\)
Bước 1: Tính \(\Delta = {b^2} - 4ac\)
Bước 2:
- Nếu \(\Delta < 0\) thì \(f(x)\) luôn cùng dấu với a với mọi \(x \in \mathbb{R}\)
- Nếu \(\Delta = 0\) thì \(f(x)\)có nghiệm kép là \({x_0}\) . Vậy \(f(x)\)cùng dấu với a với \(x \ne {x_0}\)
- Nếu \(\Delta > 0\) thì \(f(x)\)có 2 nghiệm là \({x_1};{x_2}\)\(({x_1} < {x_2})\). Ta lập bảng xét dấu.

Lời giải chi tiết:
a) \(f(x) = - 3{x^2} + x - \sqrt 2 \)có \(\Delta = 1 - 12\sqrt 2 < 0\)và a=-3<0 nên \(f(x) < 0\)với mọi \(x \in \mathbb{R}\)
b) \(g(x) = {x^2} + 8x + 16\) có \(\Delta = 0\)và a=1>0 nên g(x) có nghiệm kép \(x = - 4\) và g(x) >0 với mọi \(x \ne - 4\)
c) \(h(x) = - 2{x^2} + 7x - 3\) có \(\Delta = 25\)>0 và a=-2<0 và có 2 nghiệm phân biệt \({x_1} = \frac{1}{2};{x_2} = 3\)
Do đó ta có bảng xét dấu h(x)
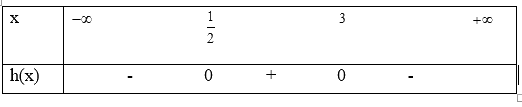
Suy ra h(x) <0 với mọi \(x \in \left( { - \infty ;\frac{1}{2}} \right) \cup \left( {3; + \infty } \right)\) và h(x)>0 với mọi \(x \in \left( {\frac{1}{2};3} \right)\)
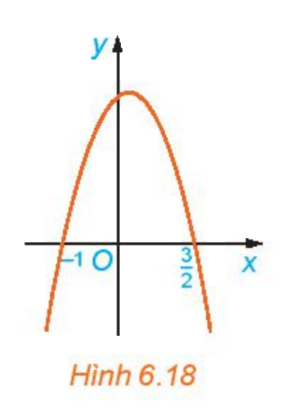
Cho đồ thị hàm số \(y = g(x) = - 2{x^3} + x + 3\) như Hình 6.18
a) Xét trên từng khoảng \(\left( { - \infty ; - 1} \right),\left( { - 1;\frac{3}{2}} \right),\left( {\frac{3}{2}; + \infty } \right)\), đồ thị nằm phía trên trục Ox hay nằm phía dưới trục Ox
b) Nhận xét về dấu của g(x) và dấu của hệ số a trên từng khoảng đó
Lời giải chi tiết:
Ta có: hệ số a=-2<0
a) Nhìn vào đồ thị ta thấy
- Trên khoảng \(\left( { - \infty ; - 1} \right)\) đồ thị nằm phía dưới trục hoành
- Trên khoảng \(\left( { - 1;\frac{3}{2}} \right)\), đồ thị nằm phía trên trục hoành
- Trên khoảng \(\left( {\frac{3}{2}; + \infty } \right)\), đồ thị nằm phía dưới trục hoành
c) - Trên khoảng \(\left( { - \infty ; - 1} \right)\) đồ thị nằm phía dưới trục hoành => f(x)<0, cùng dầu với hệ số a
- Trên khoảng \(\left( { - 1;\frac{3}{2}} \right)\), đồ thị nằm phía trên trục hoành => f(x) >0, khác dấu với hệ số a
- Trên khoảng \(\left( {\frac{3}{2}; + \infty } \right)\), đồ thị nằm phía dưới trục hoành => f(x)<0, cùng dấu với hệ số a
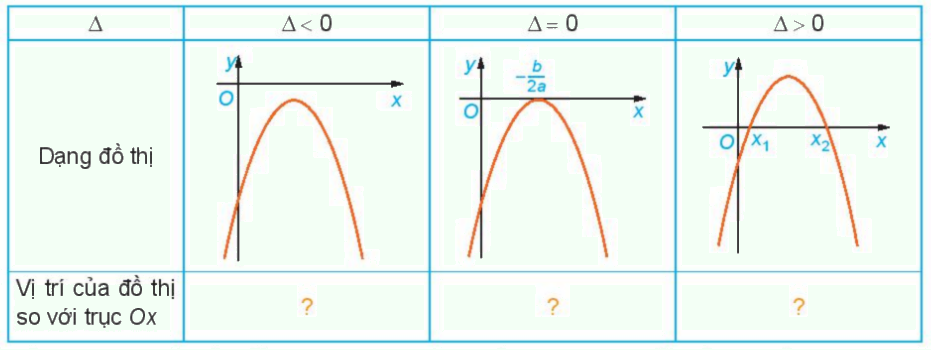
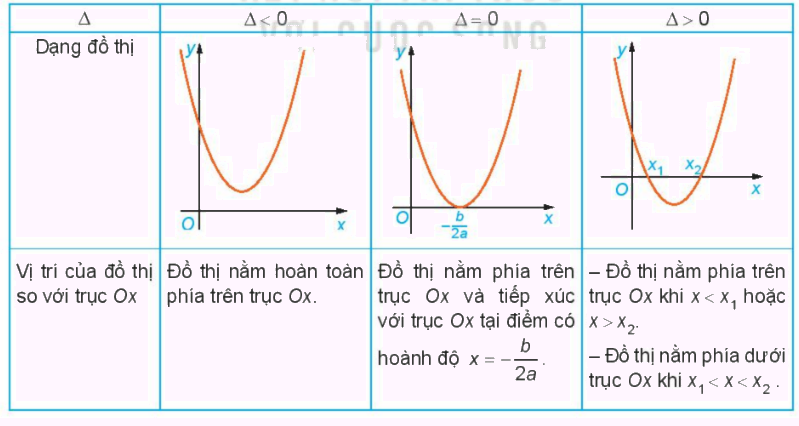
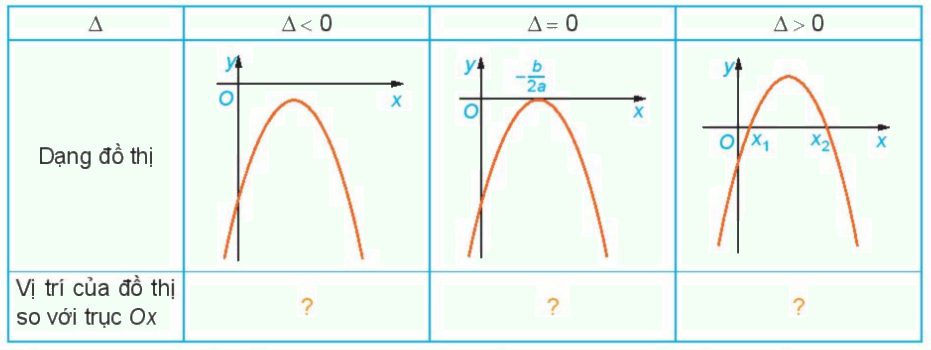
Nêu nội dung thay vào các ô có dấu “?” trong bảng sau cho thích hợp
Trường hợp a>0
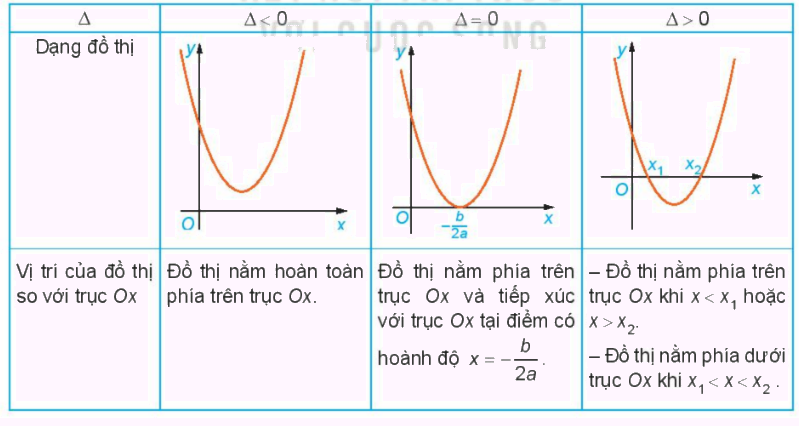
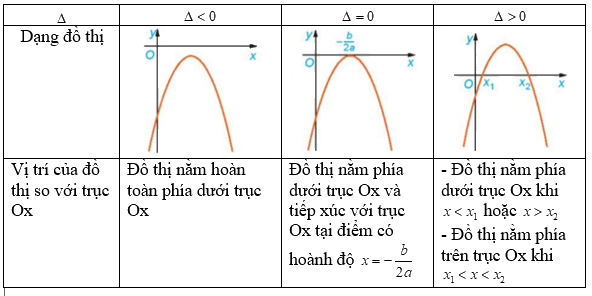
Trường hợp a<0
Lời giải chi tiết:
Hãy chỉ ra một đặc điểm chung của các biểu thức dưới đây:
\(A = 0,5{x^2}\)
\(B = 1 - {x^2}\)
\(C = {x^2} + x + 1\)
\(D = (1 - x)(2x + 1)\)
Lời giải chi tiết:
Ta có :
\(A = 0,5{x^2}\)
\(B = 1 - {x^2}\)
\(C = {x^2} + x + 1\)
\(D = (1 - x)(2x + 1) = 2x + 1 - 2{x^2} - x = - 2{x^2} + x + 1\)
=> Các biểu thức đều có dạng \(a{x^2} + bx + c(a \ne 0)\), a,b,c là các số thực.
Hãy cho biết biểu thức nào sau đây là tam thức bậc hai.
\(A = 3x + 2\sqrt x + 1\)
\(B = - 5{x^4} - 3{x^2} + 4\)
\(C = - \frac{2}{3}{x^2} + 7x - 4\)
\(D = {\left( {\frac{1}{x}} \right)^2} + 2.\frac{1}{x} + 3\)
Phương pháp giải:
Tam thức bậc hai là biểu thức có dạng \(a{x^2} + bx + c\), trong đó a,b,c là những số cho trước \(\left( {a \ne 0} \right)\)
Lời giải chi tiết:
Biểu thức \(C = - \frac{2}{3}{x^2} + 7x - 4\) là tam thức bậc hai
Biểu thức A không là tam thức bậc hai vì chứa \(\sqrt x \)
Biểu thức B không là tam thức bậc hai vì chứa \({x^4}\)
Biểu thức D không là tam thức bậc hai vì chứa \({\left( {\frac{1}{x}} \right)^2}\)
Cho hàm số bậc hai \(y = f(x) = {x^2} - 4x + 3\)
a) Xác định hệ số a. Tính \(f(0);f(1);f(2);f(3);f(4)\) và nhận xét về dấu của chúng so với dấu của hệ số a
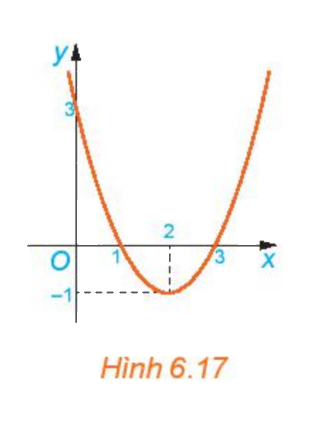
b) Cho đồ thị hàm số y=f(x) (H.6.17). Xét từng khoảng \(\left( { - \infty ;1} \right);\left( {1;3} \right);\left( {3; + \infty } \right)\), đồ thị nằm phía trên hay phía dưới trục Ox?
c) Nhận xét về dấu của f(x) và dấu của hệ số a trên từng khoảng đó.
Lời giải chi tiết:
a) Hệ số a là: a=1
\(f(0) = {0^2} - 4.0 + 3 = 3\)
\(f(1) = {1^2} - 4.1 + 3 = 0\)
\(f(2) = {2^2} - 4.2 + 3 = - 1\)
\(f(3) = {3^2} - 4.3 + 3 = 0\)
\(f(4) = {4^2} - 4.4 + 3 = 3\)
=> f(0); f(4) cùng dấu với hệ số a; f(2) khác dấu với hệ số a
b) Nhìn vào đồ thị ta thấy
- Trên khoảng \(\left( { - \infty ;1} \right)\) đồ thị nằm phía trên trục hoành
- Trên khoảng \(\left( {1;3} \right)\), đồ thị nằm phía dưới trục hoành
- Trên khoảng \(\left( {3; + \infty } \right)\), đồ thị nằm phía trên trục hoành
c) - Trên khoảng \(\left( { - \infty ;1} \right)\) đồ thị nằm phía trên trục hoành => f(x)>0, cùng dầu với hệ số a
- Trên khoảng \(\left( {1;3} \right)\), đồ thị nằm phía dưới trục hoành => f(x) <0, khác dấu với hệ số a
- Trên khoảng \(\left( {3; + \infty } \right)\), đồ thị nằm phía trên trục hoành => f(x)>0, cùng dấu với hệ số a
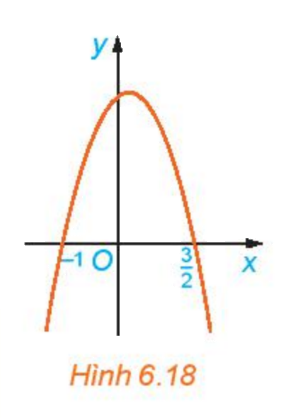
Cho đồ thị hàm số \(y = g(x) = - 2{x^3} + x + 3\) như Hình 6.18
a) Xét trên từng khoảng \(\left( { - \infty ; - 1} \right),\left( { - 1;\frac{3}{2}} \right),\left( {\frac{3}{2}; + \infty } \right)\), đồ thị nằm phía trên trục Ox hay nằm phía dưới trục Ox
b) Nhận xét về dấu của g(x) và dấu của hệ số a trên từng khoảng đó
Lời giải chi tiết:
Ta có: hệ số a=-2<0
a) Nhìn vào đồ thị ta thấy
- Trên khoảng \(\left( { - \infty ; - 1} \right)\) đồ thị nằm phía dưới trục hoành
- Trên khoảng \(\left( { - 1;\frac{3}{2}} \right)\), đồ thị nằm phía trên trục hoành
- Trên khoảng \(\left( {\frac{3}{2}; + \infty } \right)\), đồ thị nằm phía dưới trục hoành
c) - Trên khoảng \(\left( { - \infty ; - 1} \right)\) đồ thị nằm phía dưới trục hoành => f(x)<0, cùng dầu với hệ số a
- Trên khoảng \(\left( { - 1;\frac{3}{2}} \right)\), đồ thị nằm phía trên trục hoành => f(x) >0, khác dấu với hệ số a
- Trên khoảng \(\left( {\frac{3}{2}; + \infty } \right)\), đồ thị nằm phía dưới trục hoành => f(x)<0, cùng dấu với hệ số a
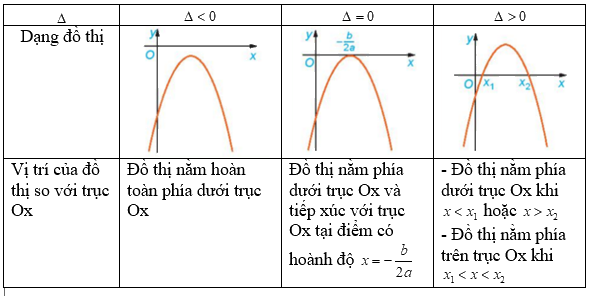
Nêu nội dung thay vào các ô có dấu “?” trong bảng sau cho thích hợp
Trường hợp a>0
Trường hợp a<0
Lời giải chi tiết:
Xét dấu các tam thức bậc hai sau:
a) \( - 3{x^2} + x - \sqrt 2 \)
b) \({x^2} + 8x + 16\)
c) \( - 2{x^2} + 7x - 3\)
Phương pháp giải:
Xét dấu tam thức bậc hai \(f(x) = a{x^2} + bx + c\)
Bước 1: Tính \(\Delta = {b^2} - 4ac\)
Bước 2:
- Nếu \(\Delta < 0\) thì \(f(x)\) luôn cùng dấu với a với mọi \(x \in \mathbb{R}\)
- Nếu \(\Delta = 0\) thì \(f(x)\)có nghiệm kép là \({x_0}\) . Vậy \(f(x)\)cùng dấu với a với \(x \ne {x_0}\)
- Nếu \(\Delta > 0\) thì \(f(x)\)có 2 nghiệm là \({x_1};{x_2}\)\(({x_1} < {x_2})\). Ta lập bảng xét dấu.

Lời giải chi tiết:
a) \(f(x) = - 3{x^2} + x - \sqrt 2 \)có \(\Delta = 1 - 12\sqrt 2 < 0\)và a=-3<0 nên \(f(x) < 0\)với mọi \(x \in \mathbb{R}\)
b) \(g(x) = {x^2} + 8x + 16\) có \(\Delta = 0\)và a=1>0 nên g(x) có nghiệm kép \(x = - 4\) và g(x) >0 với mọi \(x \ne - 4\)
c) \(h(x) = - 2{x^2} + 7x - 3\) có \(\Delta = 25\)>0 và a=-2<0 và có 2 nghiệm phân biệt \({x_1} = \frac{1}{2};{x_2} = 3\)
Do đó ta có bảng xét dấu h(x)
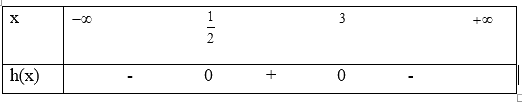
Suy ra h(x) <0 với mọi \(x \in \left( { - \infty ;\frac{1}{2}} \right) \cup \left( {3; + \infty } \right)\) và h(x)>0 với mọi \(x \in \left( {\frac{1}{2};3} \right)\)
Mục 1 của SGK Toán 10 tập 2 Kết nối tri thức giới thiệu về hàm số bậc hai, bao gồm định nghĩa, các dạng hàm số, và các tính chất cơ bản. Việc nắm vững kiến thức này là vô cùng quan trọng để giải quyết các bài toán liên quan đến hàm số bậc hai trong các chương tiếp theo.
Hàm số bậc hai có dạng tổng quát là y = ax² + bx + c, trong đó a, b, và c là các số thực, và a ≠ 0. Hàm số này được xác định khi x thuộc tập số thực. Việc xác định hệ số a, b, c là bước đầu tiên để phân tích và giải quyết các bài toán liên quan đến hàm số bậc hai.
Mỗi dạng hàm số bậc hai có những đặc điểm và phương pháp giải riêng. Việc nhận biết đúng dạng hàm số là yếu tố then chốt để áp dụng các công thức và kỹ thuật phù hợp.
Hàm số bậc hai có những tính chất quan trọng như:
Việc hiểu rõ các tính chất này giúp chúng ta vẽ được đồ thị hàm số và phân tích các bài toán liên quan.
Các bài tập trong mục 1 SGK Toán 10 tập 2 Kết nối tri thức tập trung vào việc:
Để giải các bài tập này, bạn cần nắm vững định nghĩa, các dạng hàm số, và các tính chất của hàm số bậc hai. Ngoài ra, bạn cũng cần luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
Bài tập: Cho hàm số y = 2x² - 4x + 1. Hãy xác định hệ số a, b, c và tìm trục đối xứng của hàm số.
Giải:
Hệ số a = 2, b = -4, c = 1.
Trục đối xứng của hàm số là đường thẳng x = -b/2a = -(-4)/(2*2) = 1.
Để học tốt môn Toán 10, đặc biệt là phần hàm số bậc hai, bạn nên:
Hy vọng rằng với những kiến thức và phương pháp giải bài tập được trình bày ở trên, bạn sẽ tự tin hơn khi đối mặt với các bài toán về hàm số bậc hai trong chương trình Toán 10 tập 2 Kết nối tri thức. Chúc bạn học tập tốt!