Chào mừng bạn đến với bài học lý thuyết về Ba đường conic trong chương trình Toán 10 Kết nối tri thức. Đây là một chủ đề quan trọng, đặt nền móng cho các kiến thức hình học giải tích nâng cao hơn. Bài viết này sẽ cung cấp cho bạn một cái nhìn tổng quan và chi tiết về các khái niệm, tính chất và ứng dụng của elip, hypebol và parabol.
1. Elip a) Định nghĩa elip
1. Elip
a) Định nghĩa elip
| Cho hai điểm cố định và phân biệt \({F_1}\), \({F_2}\). Đặt \({F_1}{F_2} = 2c > 0\). Cho số thực a > c. Tập hợp các điểm M sao cho \(M{F_1} + M{F_2} = 2a\) được gọi là đường elip (hay elip). Hai điểm \({F_1}\), \({F_2}\) được gọi là hai tiêu điểm và \({F_1}{F_2} = 2c\) được gọi là tiêu cự của elip đó. |
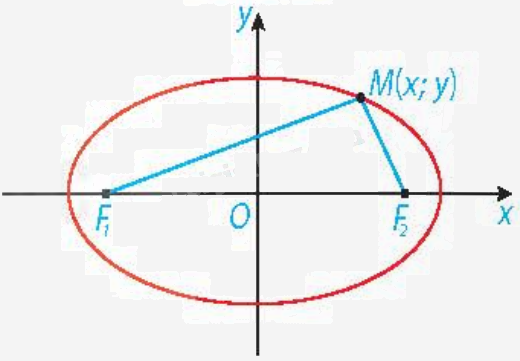
b) Phương trình chính tắc của elip
Trong mặt phẳng tọa độ Oxy, elip có hai tiêu điểm thuộc trục hoành sao cho O là trung điểm của đoạn nối hai tiêu điểm đó thì có phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\), với a > b > 0. Ngược lại, mỗi phương trình có dạng trên đều là phương trình của elip có hai tiêu điểm \({F_1}( - \sqrt {{a^2} - {b^2}} ;0)\), \({F_2}(\sqrt {{a^2} - {b^2}} ;0)\), tiêu cự \(2c = 2\sqrt {{a^2} - {b^2}} \) và tổng các khoảng cách từ mỗi điểm thuộc elip đó tới hai tiêu điểm bằng 2a. |
2. Hypebol
a) Định nghĩa hypebol
| Cho hai điểm cố định và phân biệt \({F_1}\), \({F_2}\). Đặt \({F_1}{F_2} = 2c > 0\). Cho số thực dương a < c. Tập hợp các điểm M sao cho \(\left| {M{F_1} - M{F_2}} \right| = 2a\) được gọi là đường hypebol (hay hypebol). Hai điểm \({F_1}\), \({F_2}\) được gọi là hai tiêu điểm và \({F_1}{F_2} = 2c\) được gọi là tiêu cự của hypebol đó. |
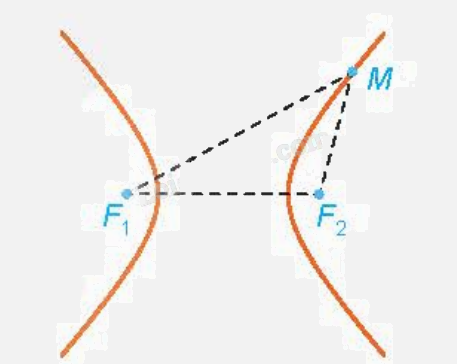
b) Phương trình chính tắc của hypebol
Trong mặt phẳng tọa độ Oxy, hypebol có hai tiêu điểm thuộc trục hoành sao cho O là trung điểm của đoạn nối hai tiêu điểm đó thì có phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\), với a > 0, b > 0. Ngược lại, mỗi phương trình có dạng trên đều là phương trình của hypebol có hai tiêu điểm \({F_1}( - \sqrt {{a^2} + {b^2}} ;0)\), \({F_2}(\sqrt {{a^2} + {b^2}} ;0)\), tiêu cự \(2c = 2\sqrt {{a^2} + {b^2}} \) và giá trị tuyệt đối của hiệu các khoảng cách từ mỗi điểm thuộc hypebol đến hai tiêu điểm bằng 2a. |
3. Parabol
a) Định nghĩa parabol
| Cho một điểm F cố định và một đường thẳng \(\Delta \) cố định không đi qua F. Tập hợp các điểm M cách đều F và \(\Delta \) được gọi là đường parabol (hay parabol). Điểm F được gọi là tiêu điểm, \(\Delta \) được gọi là đường chuẩn, khoảng cách từ F đến \(\Delta \) được gọi là tham số tiêu của parabol đó. |
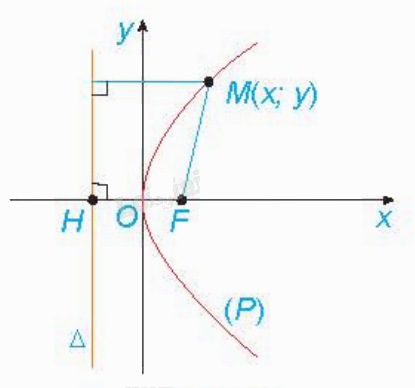
b) Phương trình chính tắc của parabol
Xét (P) là một parabol với tiêu điểm F, đường chuẩn \(\Delta \). Gọi H là hình chiếu vuông góc của F trên \(\Delta \). Khi đó, trong hệ trục tọa độ Oxy với gốc O là trung điểm của HF, tia Ox trùng tia OF, parabol (P) có phương trình chính tắc \({y^2} = 2px\) (với p > 0). Ngược lại, mỗi phương trình trên là phương trình chính tắc của parabol có tiêu điểm \(F\left( {\frac{p}{2};0} \right)\) và đường chuẩn \(\Delta :x = - \frac{p}{2}\). |
4. Một số ứng dụng của ba đường conic
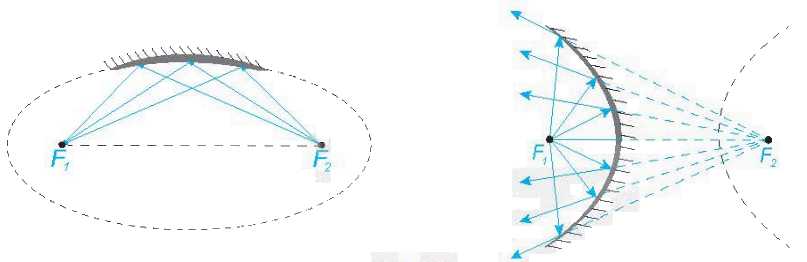
a) Tính chất quang học
Tương tự gương cầu lồi thường đặt ở những khúc đường cua, người ta cũng có những gương (lồi, lõm) elip, hypebol, parabol. Tia sáng gặp các gương này, đều được phân xạ theo một quy tắc được xác định rõ bằng hình học.
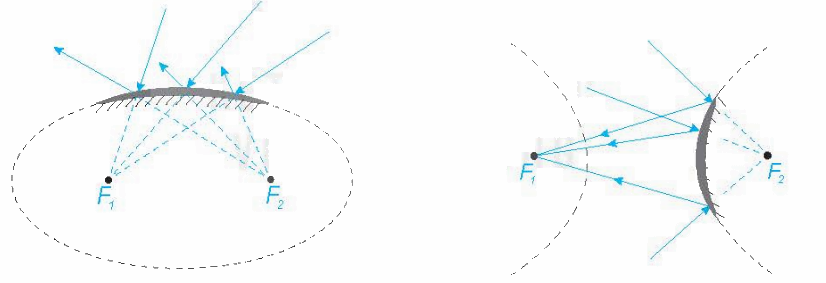
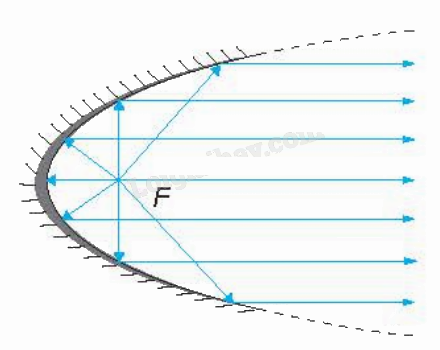
- Tia nước bắn ra từ đài phun nước, đường đi bóng của quả bóng là những hình ảnh về đường parabol;
- Khi nghiêng cốc nước hình trụ, mặt nước trong cốc có hình elip. Tương tự, dưới ánh sáng mặt trời, bóng của một quả bóng, nhìn chung, là một elip;
- Ánh sáng phát ra từ một bóng đèn Led trên trần nhà có thể tạo nên trên tường các nhánh hyperbol;
- Nhiều công trình kiến trúc có hình elip, parabol hay hyperbol.
B. Bài tập
Bài 1: Trong các phương trình sau, phương trình nào là phương trình chính tắc của elip?
a) \(\frac{{{x^2}}}{{{3^2}}} + \frac{{{y^2}}}{{{3^2}}} = 1\)
b) \(\frac{{{x^2}}}{{{4^2}}} + \frac{{{y^2}}}{{{3^2}}} = - 1\)
c) \(\frac{{{x^2}}}{{{3^2}}} + \frac{{{y^2}}}{{{4^2}}} = 1\)
d) \(\frac{{{x^2}}}{{{4^2}}} + \frac{{{y^2}}}{{{3^2}}} = 1\)
Giải:
Phương trình chính tắc của elip có dạng \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\), với a > b > 0 nên chỉ có trường hợp d) là phương trình chính tắc của elip.
Bài 2: Trong các phương trình sau, phương trình nào là phương trình chính tắc của hypebol?
a) \(\frac{{{x^2}}}{{{5^2}}} - \frac{{{y^2}}}{{{4^2}}} = - 1\)
b) \(\frac{{{x^2}}}{{{4^2}}} - \frac{{{y^2}}}{{{5^2}}} = 1\)
c) \(\frac{{{x^2}}}{{{5^2}}} - \frac{{{y^2}}}{{{5^2}}} = 1\)
d) \(\frac{{{x^2}}}{{{5^2}}} - \frac{{{y^2}}}{{{4^2}}} = 1\)
Giải:
Phương trình chính tắc của hypebol có dạng \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\), với a > 0, b > 0 nên các trường hợp b), c), d) là phương trình chính tắc của hypebol.
Bài 3: Trong các phương trình sau, phương trình nào là phương trình chính tắc của parabol?
a) \({y^2} = - 6x\)
b) \({y^2} = 6x\)
c) \({y^2} = - 6y\)
d) \({y^2} = 6y\)
Giải:
Phương trình chính tắc của parabol có dạng \({y^2} = 2px\), với p > 0 nên chỉ có trường hợp d) là phương trình chính tắc của parabol.
Bài 4: Cho elip có phương trình chính tắc \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\). Tìm các tiêu điểm và tiêu cự của elip. Tính tổng khoảng cách từ mỗi điểm trên elip tới hai tiêu điểm.
Giải:
Ta có: \({a^2} = 25\), \({b^2} = 16\). Do đó \(c = \sqrt {{a^2} - {b^2}} = 3\). Vậy elip có hai tiêu điểm là \({F_1}( - 3;0)\), \({F_2}(3;0)\) và tiêu cự là \({F_1}{F_2} = 2c = 6\). Ta có \(a = \sqrt {25} = 5\) nên tổng các khoảng cách từ mỗi điểm trên elip tới hai tiêu điểm bằng 2a = 10.
Bài 5: Cho hypebol có phương trình chính tắc \(\frac{{{x^2}}}{9} - \frac{{{y^2}}}{{16}} = 1\). Tìm các tiêu điểm và tiêu cự của hypebol. Hiệu các khoảng cách từ một điểm nằm trên hypebol tới hai tiêu điểm có giá trị tuyệt đối bằng bao nhiêu?
Giải:
Ta có: \({a^2} = 9\), \({b^2} = 16\). Do đó \(c = \sqrt {{a^2} + {b^2}} = 5\). Vậy hypebol có hai tiêu điểm là \({F_1}( - 5;0)\), \({F_2}(5;0)\) và tiêu cự là \(2c = 10\). Hiệu các khoảng cách từ một điểm nằm trên hypebol tới hai tiêu điểm có giá trị tuyệt đối bằng \(2a = 2\sqrt 9 = 6\).
Bài 6: Cho parabol (P): \({y^2} = x\).
a) Tìm tiêu điểm F, đường chuẩn \(\Delta \) của (P).
b) Tìm những điểm trên (P) có khoảng cách tới F bằng 3.
Giải:
a) Ta có \(2p = 1\) nên \(p = \frac{1}{2}\).
Parabol có tiêu điểm \(F\left( {\frac{1}{4};0} \right)\) và đường chuẩn \(\Delta :x = - \frac{1}{4}\).
b) Điểm \(M({x_0};{y_0})\) thuộc (P) có khoảng cách tới F bằng 3 khi và chỉ khi \({y_0}^2 = {x_0}\) và MF = 3. Do \(MF = d(M,\Delta )\) nên \(d(M,\Delta ) = 3\).
Mặt khác \(\Delta :x = - \frac{1}{4}\) và \({x_0} = {y_0}^2 \ge 0\) nên \(3 = d(M,\Delta ) = \left| {{x_0} + \frac{1}{4}} \right| = {x_0} + \frac{1}{4}\).
Vậy \({x_0} = \frac{{11}}{4}\) và \({y_0} = \frac{{\sqrt {11} }}{2}\) hoặc \({y_0} = - \frac{{\sqrt {11} }}{2}\).
Vậy có hai điểm M thỏa mãn bài toán với tọa độ là \(\left( {\frac{{11}}{4};\frac{{\sqrt {11} }}{2}} \right)\) và \(\left( {\frac{{11}}{4}; - \frac{{\sqrt {11} }}{2}} \right)\).
Bài 7: Lập phương trình chính tắc của elip (E) có một tiêu điểm là \({F_2}(5;0)\) và đi qua điểm M(0;3).
Giải:
Elip (E) có phương trình chính tắc là \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) (a > b > 0).
Do \({F_2}(5;0)\) là một tiêu điểm của (E) nên c = 5.
Điểm M(0;3) nằm trên (E) nên \(\frac{{{0^2}}}{{{a^2}}} + \frac{{{3^2}}}{{{b^2}}} = 1\). Do đó \({b^2} = 9\).
Suy ra \({a^2} = {b^2} + {c^2} = 9 + 25 = 34\).
Vậy elip (E) có phương trình chính tắc là \(\frac{{{x^2}}}{{34}} + \frac{{{y^2}}}{9} = 1\).
Bài 8: Lập phương trình chính tắc của hypebol (H) có một tiêu điểm là \({F_2}(6;0)\) và đi qua điểm A(4;0).
Giải:
Hypebol (H) có phương trình chính tắc là \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) (a > 0, b > 0).
Do \({F_2}(6;0)\) là một tiêu điểm của (H) nên c = 6.
Điểm A(4;0) nằm trên (H) nên \(\frac{{{4^2}}}{{{a^2}}} - \frac{{{0^2}}}{{{b^2}}} = 1\). Do đó \({a^2} = 16\).
Suy ra \({b^2} = {c^2} - {a^2} = {6^2} - 16 = 20\).
Vậy hypebol (H) có phương trình chính tắc là \(\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{{20}} = 1\).
Bài 9: Lập phương trình chính tắc của parabol (P), biết:
a) (P) có tiêu điểm là F(5;0).
b) (P) đi qua điểm M(2;1).
Giải:
Parabol (P) có phương trình chính tắc là \({y^2} = 2px\) (p > 0).
a) Do F(5;0) là tiêu điểm của (P) nên \(\frac{p}{2} = 5\), tức là p = 10.
Vậy parabol (P) có phương trình chính tắc là \({y^2} = 20x\).
b) M(2;1) nằm trên (P) nên \({1^2} = 2p.2\), tức \(p = \frac{1}{4}\).
Vậy parabol (P) có phương trình chính tắc là \({y^2} = \frac{x}{2}\).
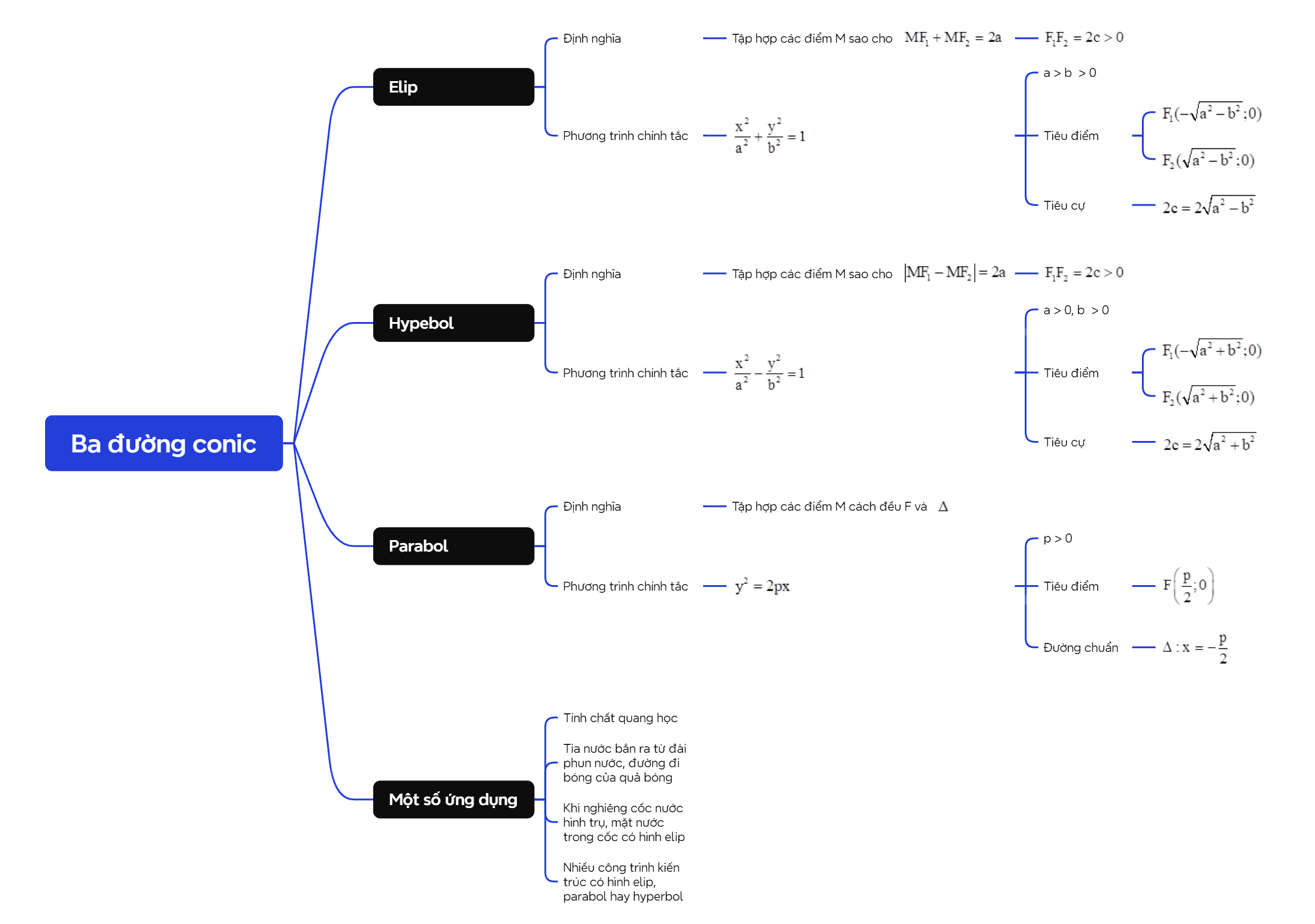
Ba đường conic, bao gồm elip, hypebol và parabol, là những đường cong quan trọng trong hình học giải tích. Chúng được định nghĩa dựa trên một điểm cố định (tiêu điểm) và một đường thẳng cố định (đường chuẩn). Việc hiểu rõ lý thuyết về ba đường conic là rất quan trọng để giải quyết các bài toán liên quan đến quỹ đạo của các vật thể chuyển động, thiết kế các công trình kiến trúc và nhiều ứng dụng khác.
Định nghĩa: Elip là tập hợp tất cả các điểm M sao cho tổng khoảng cách từ M đến hai điểm cố định F1 và F2 (tiêu điểm) là một hằng số (2a).
Phương trình chính tắc:\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 (với a > b > 0)
Tính chất:
Định nghĩa: Hypebol là tập hợp tất cả các điểm M sao cho trị tuyệt đối hiệu khoảng cách từ M đến hai điểm cố định F1 và F2 (tiêu điểm) là một hằng số (2a).
Phương trình chính tắc:\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 (với a > 0, b > 0)
Tính chất:
Định nghĩa: Parabol là tập hợp tất cả các điểm M sao cho khoảng cách từ M đến một điểm cố định F (tiêu điểm) bằng khoảng cách từ M đến một đường thẳng cố định Δ (đường chuẩn).
Phương trình chính tắc:y^2 = 2px (với p > 0)
Tính chất:
Ba đường conic (elip, hypebol, parabol) đều là các mặt cắt của một hình nón tròn xoay bởi một mặt phẳng. Tùy thuộc vào góc nghiêng của mặt phẳng so với trục của hình nón, ta sẽ thu được một trong ba đường conic:
Ba đường conic có rất nhiều ứng dụng trong thực tế:
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và quan trọng về lý thuyết Ba đường conic. Hãy luyện tập thêm các bài tập để nắm vững kiến thức và áp dụng vào giải quyết các bài toán thực tế.