Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 tập 1 của giaitoan.edu.vn. Trong bài viết này, chúng ta sẽ cùng nhau giải chi tiết các bài tập trong mục 3 trang 8 và 9 sách giáo khoa Toán 10 tập 1 - Kết nối tri thức.
Mục tiêu của chúng tôi là cung cấp cho các em những lời giải chính xác, dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Cặp từ quan hệ nào sau đây phù hợp với vị trí bị che khuất trong câu ghép ở hình bên? Cho hai câu sau: P: “Tam giác ABC là tam giác vuông tại A” Xét hai câu sau: P: “Phương trình bậc hai ax^2 + bx + c = 0 có hai nghiệm phân biệt” Cho các mệnh đề P: “a và b chia hết cho c”
Xét hai câu sau:
P: “Phương trình bậc hai \(a{x^2} + bx + c = 0\) có hai nghiệm phân biệt”;
Q: “Phương trình bậc hai \(a{x^2} + bx + c = 0\) có biệt thức \(\Delta = {b^2} - 4ac\;\, > 0\)”.
a) Hãy phát biểu mệnh đề \(P \Rightarrow Q\).
b) Hãy phát biểu mệnh đề \(Q \Rightarrow P\).
Phương pháp giải:
Mệnh đề \(P \Rightarrow Q\) thường phát biểu ở dạng: “Nếu P thì Q”, “P suy ra Q”, “Vì P nên Q”.
Mệnh đề \(Q \Rightarrow P\) thường phát biểu ở dạng: “Nếu Q thì P”, “Q suy ra P”, “Vì Q nên P”.
Thay P, Q lần lượt bởi nội dung mệnh đề vào câu ghép.
Lời giải chi tiết:
Mệnh đề \(P \Rightarrow Q\): “Nếu phương trình bậc hai \(a{x^2} + bx + c = 0\) có hai nghiệm phân biệt thì phương trình bậc hai \(a{x^2} + bx + c = 0\) có biệt thức \(\Delta = {b^2} - 4ac\;\, > 0\).”
Mệnh đề \(Q \Rightarrow P\): “Nếu phương trình bậc hai \(a{x^2} + bx + c = 0\) có biệt thức \(\Delta = {b^2} - 4ac\;\, > 0\) thì phương trình bậc hai \(a{x^2} + bx + c = 0\) có hai nghiệm phân biệt.”
Cho các mệnh đề
P: “a và b chia hết cho c”;
Q: “a + b chia hết cho c”.
a) Hãy phát biểu định lí \(P \Rightarrow Q\). Nêu giả thiết, kết luận của định lí và phát biểu định lí này dưới dạng điều kiện cần, điều kiện đủ.
b) Hãy phát biểu mệnh đề đảo của mệnh đề \(P \Rightarrow Q\) rồi xác định tính đúng sai của mệnh đề đảo này.
Phương pháp giải:
Nếu một mệnh đề đúng có dạng \(P \Rightarrow Q\) đúng, ta nói: P là giả thiết, Q là kết luận hoặc “P là điều kiện cần để có Q” hoặc “Q là điều kiện cần để có P”.
Mệnh đề đảo của mệnh đề \(P \Rightarrow Q\) là mệnh đề \(Q \Rightarrow P\).
Lời giải chi tiết:
a) Mệnh đề \(P \Rightarrow Q\), phát biểu là: “Nếu a và b chia hết cho c thì a + b chia hết cho c.”
Mệnh đề này đúng nên nó là một định lý.
Giả thiết của định lí: a và b chia hết cho c
Kết luận của định lí: a + b chia hết cho c
Phát biểu định lí dưới dạng điều kiện cần là: “ a + b chia hết cho c là điều kiện cần để có a và b chia hết cho c”
Phát biểu định lí dưới dạng điều kiện đủ là: “ a và b chia hết cho c là điều kiện đủ để có a + b chia hết cho c”
b) Mệnh đề đảo của mệnh đề \(P \Rightarrow Q\) là mệnh đề \(Q \Rightarrow P\).
Mệnh đề \(Q \Rightarrow P\): “Nếu a + b chia hết cho c thì a và b chia hết cho c”
Mệnh đề này sai.
Chẳng hạn a = 1 và b = 2, c =3. Ta có: \(1 + 2 = 3\; \vdots \;3\), nhưng 1 và 2 không chia hết cho 3.
Cho hai câu sau:
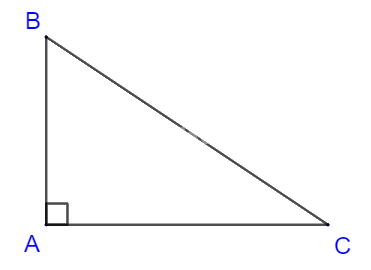
P: “Tam giác ABC là tam giác vuông tại A”;
Q: “Tam giác ABC có \(A{B^2} + A{C^2} = B{C^2}\)”.
Hãy phát biểu câu ghép có dạng “Nếu P thì Q”.
Phương pháp giải:
Thay P, Q lần lượt bởi nội dung mệnh đề của nó.
Lời giải chi tiết:
Phát biểu câu ghép "Nếu P thì Q" là: “Nếu tam giác ABC là tam giác vuông tại A thì tam giác ABC có \(A{B^2} + A{C^2} = B{C^2}\).”
Cặp từ quan hệ nào sau đây phù hợp với vị trí bị che khuất trong câu ghép ở hình bên?
A. Nếu … thì …
B. Tuy … nhưng …

Lời giải chi tiết:
Chọn A. Nếu … thì …
Nếu sử dụng rượu bia khi tham gia giao thông thì có thể bị xử phạt hành chính hoặc xử lí hình sự tùy theo mức độ vi phạm.
Cặp từ quan hệ nào sau đây phù hợp với vị trí bị che khuất trong câu ghép ở hình bên?
A. Nếu … thì …
B. Tuy … nhưng …

Lời giải chi tiết:
Chọn A. Nếu … thì …
Nếu sử dụng rượu bia khi tham gia giao thông thì có thể bị xử phạt hành chính hoặc xử lí hình sự tùy theo mức độ vi phạm.
Cho hai câu sau:
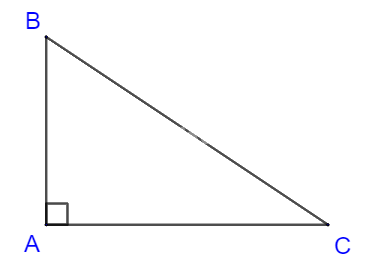
P: “Tam giác ABC là tam giác vuông tại A”;
Q: “Tam giác ABC có \(A{B^2} + A{C^2} = B{C^2}\)”.
Hãy phát biểu câu ghép có dạng “Nếu P thì Q”.
Phương pháp giải:
Thay P, Q lần lượt bởi nội dung mệnh đề của nó.
Lời giải chi tiết:
Phát biểu câu ghép "Nếu P thì Q" là: “Nếu tam giác ABC là tam giác vuông tại A thì tam giác ABC có \(A{B^2} + A{C^2} = B{C^2}\).”
Xét hai câu sau:
P: “Phương trình bậc hai \(a{x^2} + bx + c = 0\) có hai nghiệm phân biệt”;
Q: “Phương trình bậc hai \(a{x^2} + bx + c = 0\) có biệt thức \(\Delta = {b^2} - 4ac\;\, > 0\)”.
a) Hãy phát biểu mệnh đề \(P \Rightarrow Q\).
b) Hãy phát biểu mệnh đề \(Q \Rightarrow P\).
Phương pháp giải:
Mệnh đề \(P \Rightarrow Q\) thường phát biểu ở dạng: “Nếu P thì Q”, “P suy ra Q”, “Vì P nên Q”.
Mệnh đề \(Q \Rightarrow P\) thường phát biểu ở dạng: “Nếu Q thì P”, “Q suy ra P”, “Vì Q nên P”.
Thay P, Q lần lượt bởi nội dung mệnh đề vào câu ghép.
Lời giải chi tiết:
Mệnh đề \(P \Rightarrow Q\): “Nếu phương trình bậc hai \(a{x^2} + bx + c = 0\) có hai nghiệm phân biệt thì phương trình bậc hai \(a{x^2} + bx + c = 0\) có biệt thức \(\Delta = {b^2} - 4ac\;\, > 0\).”
Mệnh đề \(Q \Rightarrow P\): “Nếu phương trình bậc hai \(a{x^2} + bx + c = 0\) có biệt thức \(\Delta = {b^2} - 4ac\;\, > 0\) thì phương trình bậc hai \(a{x^2} + bx + c = 0\) có hai nghiệm phân biệt.”
Cho các mệnh đề
P: “a và b chia hết cho c”;
Q: “a + b chia hết cho c”.
a) Hãy phát biểu định lí \(P \Rightarrow Q\). Nêu giả thiết, kết luận của định lí và phát biểu định lí này dưới dạng điều kiện cần, điều kiện đủ.
b) Hãy phát biểu mệnh đề đảo của mệnh đề \(P \Rightarrow Q\) rồi xác định tính đúng sai của mệnh đề đảo này.
Phương pháp giải:
Nếu một mệnh đề đúng có dạng \(P \Rightarrow Q\) đúng, ta nói: P là giả thiết, Q là kết luận hoặc “P là điều kiện cần để có Q” hoặc “Q là điều kiện cần để có P”.
Mệnh đề đảo của mệnh đề \(P \Rightarrow Q\) là mệnh đề \(Q \Rightarrow P\).
Lời giải chi tiết:
a) Mệnh đề \(P \Rightarrow Q\), phát biểu là: “Nếu a và b chia hết cho c thì a + b chia hết cho c.”
Mệnh đề này đúng nên nó là một định lý.
Giả thiết của định lí: a và b chia hết cho c
Kết luận của định lí: a + b chia hết cho c
Phát biểu định lí dưới dạng điều kiện cần là: “ a + b chia hết cho c là điều kiện cần để có a và b chia hết cho c”
Phát biểu định lí dưới dạng điều kiện đủ là: “ a và b chia hết cho c là điều kiện đủ để có a + b chia hết cho c”
b) Mệnh đề đảo của mệnh đề \(P \Rightarrow Q\) là mệnh đề \(Q \Rightarrow P\).
Mệnh đề \(Q \Rightarrow P\): “Nếu a + b chia hết cho c thì a và b chia hết cho c”
Mệnh đề này sai.
Chẳng hạn a = 1 và b = 2, c =3. Ta có: \(1 + 2 = 3\; \vdots \;3\), nhưng 1 và 2 không chia hết cho 3.
Mục 3 trong SGK Toán 10 tập 1 - Kết nối tri thức tập trung vào các khái niệm cơ bản về tập hợp số, bao gồm tập số thực, các phép toán trên tập số thực, và các tính chất của chúng. Việc nắm vững kiến thức này là nền tảng quan trọng cho các chương trình học toán ở các lớp trên.
Bài tập này yêu cầu học sinh thực hiện các phép toán cộng, trừ, nhân, chia trên các số thực. Để giải bài tập này, học sinh cần nắm vững các quy tắc về dấu của số thực, thứ tự thực hiện các phép toán, và các tính chất giao hoán, kết hợp, phân phối của các phép toán.
Bài tập này yêu cầu học sinh biểu diễn các số thực trên trục số. Để giải bài tập này, học sinh cần hiểu rõ khái niệm về trục số, cách xác định vị trí của một số thực trên trục số, và cách so sánh các số thực.
Bài tập này yêu cầu học sinh so sánh các số thực. Để giải bài tập này, học sinh cần nắm vững các quy tắc về so sánh các số thực, bao gồm so sánh các số dương, so sánh các số âm, và so sánh các số dương và số âm.
| Số thực a | Số thực b | Kết quả so sánh |
|---|---|---|
| 3.5 | 2.8 | a > b |
| -4.2 | -3.7 | a < b |
Ngoài các bài tập cơ bản như trên, còn có một số dạng bài tập thường gặp trong mục 3, bao gồm:
Để giải bài tập trong mục 3 một cách hiệu quả, học sinh nên:
Hy vọng rằng với những hướng dẫn chi tiết và các ví dụ minh họa trên, các em học sinh đã có thể tự tin giải các bài tập trong mục 3 trang 8, 9 SGK Toán 10 tập 1 - Kết nối tri thức. Chúc các em học tập tốt!