Bài 3.9 trang 43 SGK Toán 10 tập 1 thuộc chương 3: Hàm số và đồ thị. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai, điều kiện xác định và cách xác định tập giá trị của hàm số.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh hiểu rõ bản chất bài toán và tự tin giải các bài tập tương tự.
Trên nóc một tòa nhà có một cột ăng-ten cao 5m. Từ một vị trí quan sát A cao 7 m so với mặt đất có thể nhìn thấy đỉnh B và chân C của cột ăng-ten, với các góc tương ứng là 50 và 40 so với phương nằm ngang (H.3.18). a) Tính các góc của tam giác ABC. b) Tính chiều cao của tòa nhà.
b) Tính chiều cao của tòa nhà.
Phương pháp giải:
Bước 1: Tính AB: \(AB = \frac{{BC.\sin C}}{{\sin A}}\)
Bước 2: Tính BH => chiều cao của tòa nhà = BH + độ cao của vị trí quan sát.
Lời giải chi tiết:
Áp dụng định lý sin cho tam giác ABC, ta được:
\(\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}}\) \( \Rightarrow AB = \frac{{BC.\sin C}}{{\sin A}}\)
Mà: \(BC = 5\;(m);\;\;\widehat C = {130^o};\;\widehat A = {10^o}\)
\( \Rightarrow AB = \frac{{5.\sin {{130}^o}}}{{\sin {{10}^o}}} \approx 22\;(m)\)
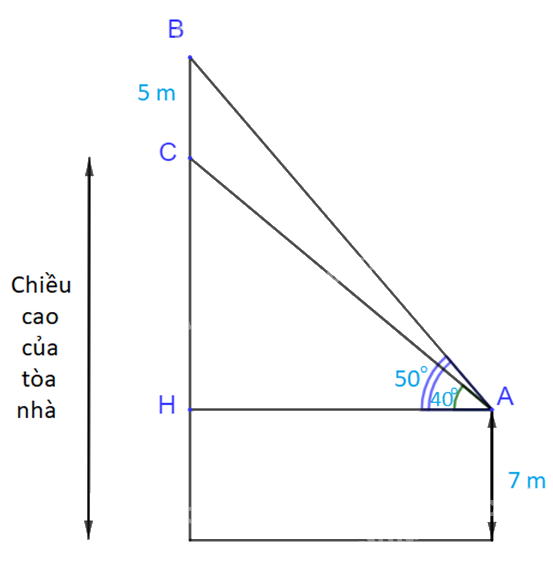
Xét tam giác ABH, vuông tại H ta có:
\(\sin \widehat {BAH} = \frac{{BH}}{{AB}}\)\( \Rightarrow BH = AB.\,\,\sin \widehat {BAH}\)
Mà: \(AB \approx 22\;(m);\;\;\widehat {BAH} = {50^o}\)
\( \Rightarrow BH \approx 22.\sin {50^o} \approx 16,85\;(m)\)
Vậy chiều cao của tòa nhà là: \(BH-{\rm{ }}BC + 7 = 16,85-5 + 7 = 18,85{\rm{ }}\left( m \right)\)
a) Tính các góc của tam giác ABC.
Phương pháp giải:
Nhắc lại: Tổng ba góc của một tam giác luôn bằng \({180^o}\).
Bước 1: Gọi H là hình chiếu của A lên đường thẳng BC.
Bước 2: Tính góc \(\widehat {BAC}\), góc \(\widehat {ABC}\) => góc \(\widehat {BCA}\).
Lời giải chi tiết:
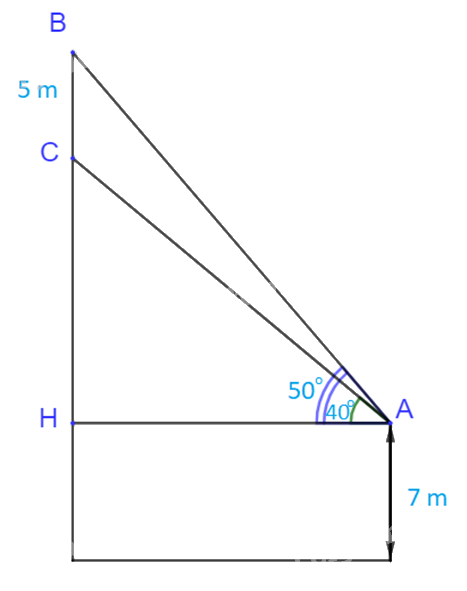
Gọi H là hình chiếu của A lên đường thẳng BC.
Ta có: \(\widehat {HAB} = {50^o}\); \(\widehat {HAC} = {40^o}\)
\( \Rightarrow \widehat {BAC} = {50^o} - {40^o} = {10^o}\) (1)
Xét tam giác ABH, vuông tại H ta có:
\(\widehat H = {90^o};\;\widehat {BAH} = {50^o}.\)
\( \Rightarrow \widehat {HBA} = {180^o} - {90^o} - {50^o} = {40^o}\) hay \(\widehat {CBA} = {40^o}\). (2)
Từ (1) và (2), suy ra: \(\widehat {BCA} = {180^o} - {40^o} - {10^o} = {130^o}.\)
Vậy ba góc của tam giác ABC lần lượt là: \(\widehat A = {10^o};\;\widehat B = {40^o};\;\widehat C = {130^o}\).
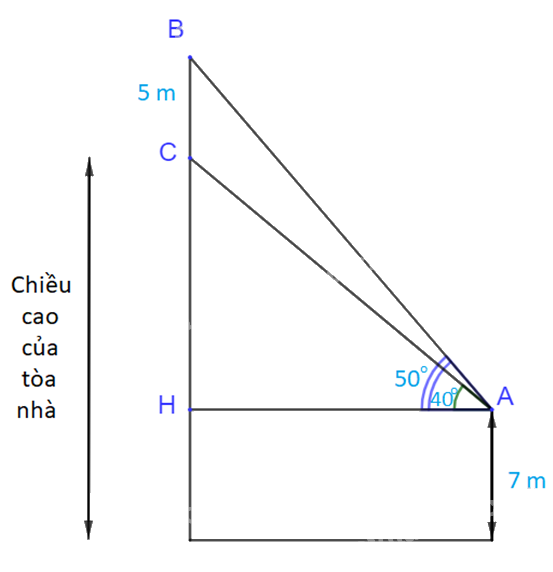
Trên nóc một tòa nhà có một cột ăng-ten cao 5m. Từ một vị trí quan sát A cao 7 m so với mặt đất có thể nhìn thấy đỉnh B và chân C của cột ăng-ten, với các góc tương ứng là \({50^o}\)và \({40^o}\) so với phương nằm ngang (H.3.18).
a) Tính các góc của tam giác ABC.
b) Tính chiều cao của tòa nhà.
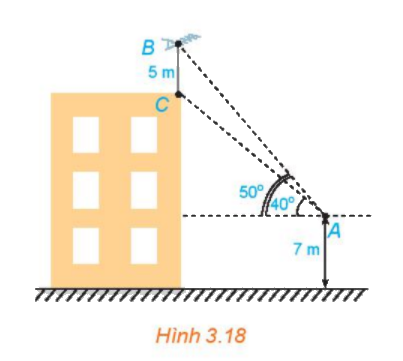
a) Tính các góc của tam giác ABC.
Phương pháp giải:
Nhắc lại: Tổng ba góc của một tam giác luôn bằng \({180^o}\).
Bước 1: Gọi H là hình chiếu của A lên đường thẳng BC.
Bước 2: Tính góc \(\widehat {BAC}\), góc \(\widehat {ABC}\) => góc \(\widehat {BCA}\).
Lời giải chi tiết:
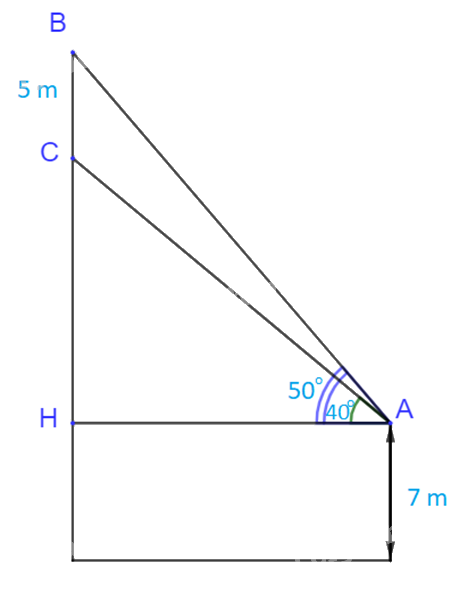
Gọi H là hình chiếu của A lên đường thẳng BC.
Ta có: \(\widehat {HAB} = {50^o}\); \(\widehat {HAC} = {40^o}\)
\( \Rightarrow \widehat {BAC} = {50^o} - {40^o} = {10^o}\) (1)
Xét tam giác ABH, vuông tại H ta có:
\(\widehat H = {90^o};\;\widehat {BAH} = {50^o}.\)
\( \Rightarrow \widehat {HBA} = {180^o} - {90^o} - {50^o} = {40^o}\) hay \(\widehat {CBA} = {40^o}\). (2)
Từ (1) và (2), suy ra: \(\widehat {BCA} = {180^o} - {40^o} - {10^o} = {130^o}.\)
Vậy ba góc của tam giác ABC lần lượt là: \(\widehat A = {10^o};\;\widehat B = {40^o};\;\widehat C = {130^o}\).
b) Tính chiều cao của tòa nhà.
Phương pháp giải:
Bước 1: Tính AB: \(AB = \frac{{BC.\sin C}}{{\sin A}}\)
Bước 2: Tính BH => chiều cao của tòa nhà = BH + độ cao của vị trí quan sát.
Lời giải chi tiết:
Áp dụng định lý sin cho tam giác ABC, ta được:
\(\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}}\) \( \Rightarrow AB = \frac{{BC.\sin C}}{{\sin A}}\)
Mà: \(BC = 5\;(m);\;\;\widehat C = {130^o};\;\widehat A = {10^o}\)
\( \Rightarrow AB = \frac{{5.\sin {{130}^o}}}{{\sin {{10}^o}}} \approx 22\;(m)\)
Xét tam giác ABH, vuông tại H ta có:
\(\sin \widehat {BAH} = \frac{{BH}}{{AB}}\)\( \Rightarrow BH = AB.\,\,\sin \widehat {BAH}\)
Mà: \(AB \approx 22\;(m);\;\;\widehat {BAH} = {50^o}\)
\( \Rightarrow BH \approx 22.\sin {50^o} \approx 16,85\;(m)\)
Vậy chiều cao của tòa nhà là: \(BH-{\rm{ }}BC + 7 = 16,85-5 + 7 = 18,85{\rm{ }}\left( m \right)\)
Bài 3.9 yêu cầu chúng ta xét hàm số f(x) = -2x2 + 8x - 5 và thực hiện các yêu cầu sau:
Hàm số f(x) = -2x2 + 8x - 5 là một hàm số bậc hai. Hệ số a = -2 < 0, do đó parabol có dạng mở xuống dưới.
Tọa độ đỉnh của parabol y = ax2 + bx + c là I(-b/2a, -Δ/4a). Trong trường hợp này, a = -2, b = 8, c = -5.
Vậy tọa độ đỉnh của parabol là I(2, 3).
Trục đối xứng của parabol là đường thẳng x = xI = 2.
Vì a = -2 < 0, hàm số nghịch biến trên khoảng (-∞, 2) và đồng biến trên khoảng (2, +∞).
Vì parabol có dạng mở xuống dưới, giá trị lớn nhất của hàm số là tung độ đỉnh, tức là 3. Hàm số không có giá trị nhỏ nhất.
Khi giải các bài tập về hàm số bậc hai, cần nắm vững các kiến thức cơ bản về:
Để củng cố kiến thức, các em có thể tự giải các bài tập tương tự trong SGK Toán 10 tập 1 – Kết nối tri thức hoặc các đề thi thử Toán 10.
Bài 3.9 trang 43 SGK Toán 10 tập 1 – Kết nối tri thức là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hàm số bậc hai và các tính chất của nó. Hy vọng với lời giải chi tiết và hướng dẫn trên, các em sẽ tự tin giải bài tập này và các bài tập tương tự.