Bài 2.15 trang 32 SGK Toán 10 tập 1 thuộc chương trình Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ và các phép toán vectơ. Bài tập này thường yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 2.15 trang 32 SGK Toán 10 tập 1, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Bác An đầu tư 1,2 tỉ đồng vào ba loại trái phiếu, trái phiếu chính phủ với lãi suất 7% một năm, trái phiếu ngân hàng với lãi suất 8% một năm và trái phiếu doanh nghiệp rủi ro cao với lãi suất 12% một năm.
Đề bài
Bác An đầu tư 1,2 tỉ đồng vào ba loại trái phiếu, trái phiếu chính phủ với lãi suất 7% một năm, trái phiếu ngân hàng với lãi suất 8% một năm và trái phiếu doanh nghiệp rủi ro cao với lãi suất 12% một năm. Vì lí do giảm thuế, bác An muốn số tiền đầu tư trái phiếu chính phủ gấp ít nhất 3 lần số tiền đầu tư trái phiếu ngân hàng. Hơn nữa, để giảm thiểu rủi ro, bác An đầu tư không quá 200 triệu đồng cho trái phiếu doanh nghiệp. Hỏi bác An nên đầu tư mỗi loại trái phiếu bao nhiêu tiền để lợi nhuận thu được sau một năm là lớn nhất?
Lời giải chi tiết
Cách 1:
Gọi x là số tiền mua trái phiếu chính phủ và y là số tiền mua trái phiếu ngân hàng. (đơn vị triệu đồng) (\(x,y \le 1200\))
Khi đó, số tiền mua trái phiếu doanh nghiệp là \(1200 - x - y\)(triệu đồng)
Vì số tiền đầu tư trái phiếu chính phủ gấp ít nhất 3 lần số tiền đầu tư trái phiếu ngân hàng nên \(x \ge 3y\)
Vì bác An đầu tư không quá 200 triệu đồng cho trái phiếu doanh nghiệp nên \(1200 - x - y \le 200 \Leftrightarrow x + y \ge 1000\)
Từ điều kiện của bài toán ta có số tiền bác An đầu tư trái phiếu phải thỏa mãn hệ:
\(\left\{ {\begin{array}{*{20}{l}}{0 \le x \le 1200}\\{0 \le y \le 1200}\\{x + y \ge 1000}\\{x - 3y \ge 0}\end{array}} \right.\)
Biểu diễn miền nghiệm của hệ trong mp tọa độ ta được
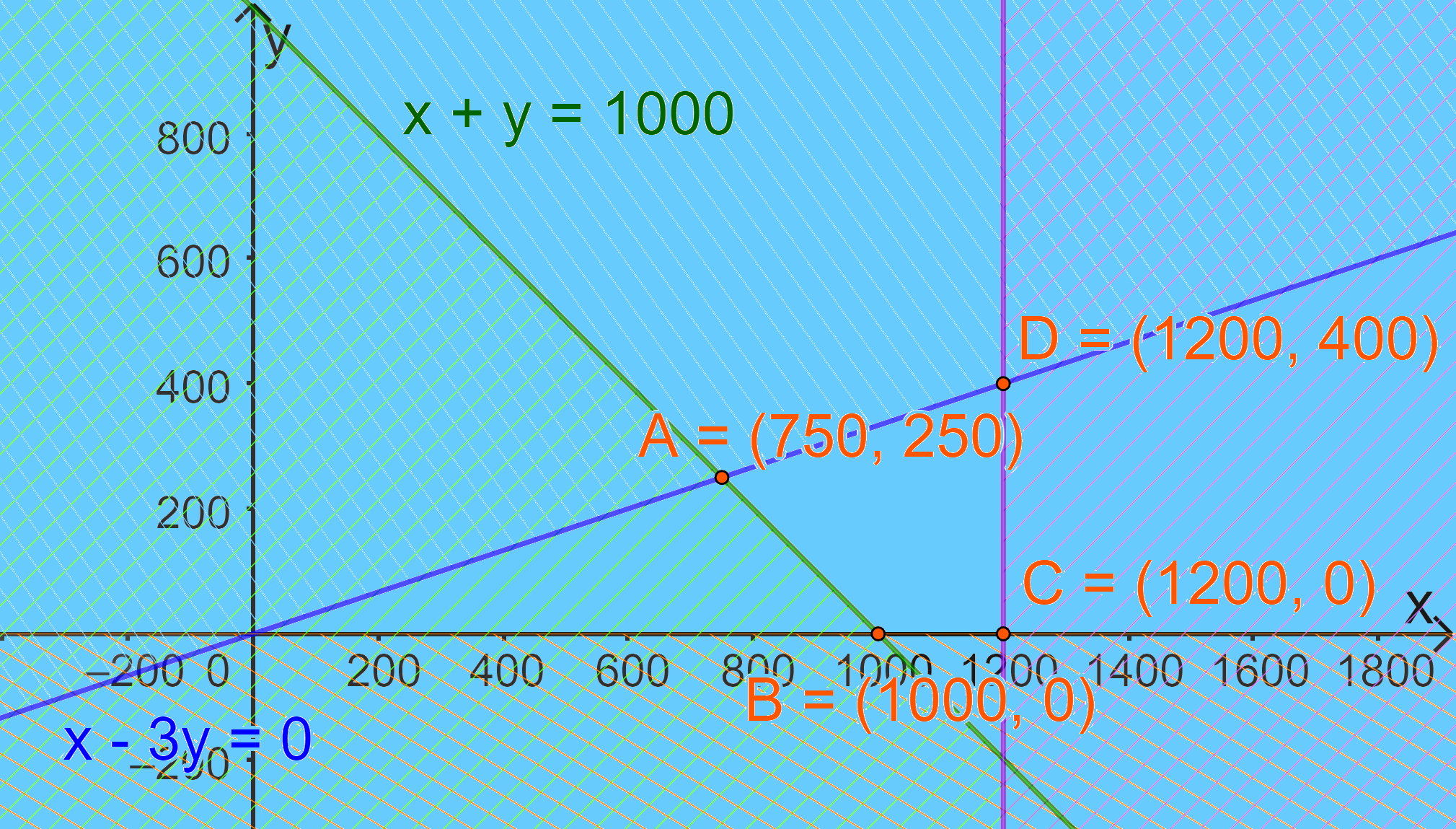
Miền nghiệm là miền tứ giác ABCD với: A(750;250); B(1000;0); C(1200;0); D(1200;400)
Lợi nhuận thu được sau một năm là
\(\begin{array}{*{20}{l}}{F\left( {x;y} \right) = x.7\% \; + y.8\% \; + (1200 - x - y).12\% }\\{ = 144 - 0,05x - 0,04y}\end{array}\)
Ta cần tìm giá trị lớn nhất của F(x;y) khi (x;y) thỏa mãn hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{0 \le x \le 1200}\\{0 \le y \le 1200}\\{x + y \ge 1000}\\{x - 3y \ge 0}\end{array}} \right.\)
Thay tọa độ các điểm A, B vào biểu thức F(x;y) ta được:
\(F\left( {750;250} \right) = 144 - 0,05.750 - 0,04.250 = 96,5\)
\(F\left( {1000;0} \right) = 144 - 0,05.1000 - 0,04.0 = 94\)
\(F\left( {1200;0} \right) = 144 - 0,05.1200 - 0,04.0 = 84\)
\(F\left( {1200;400} \right) = 144 - 0,05.1200 - 0,04.400 = 68\)
=> F đạt giá trị lớn nhất là 96,5 nếu x=750 và y=250.
Vậy bác An nên đầu tư 750 trái phiếu chính phủ; 250 triệu đồng trái phiếu ngân hàng và 200 triệu trái phiếu doanh nghiệp.
Cách 2:
Bước 1: 1,2 tỉ đồng=1200 (triệu đồng)
Gọi x là số tiền mua trái phiếu ngân hàng và y là số tiền mua trái phiếu doanh nghiệp.
Khi đó \(x \ge 0,y \ge 0\).
Bác An đầu tư 1,2 tỉ đồng vào ba loại trái phiếu, trái phiếu chính phủ nên số tiền đầu tư trái phiếu chính phủ là \(1200 - x - y\) (triệu đồng)
Số tiền đầu tư trái phiếu chính phủ gấp ít nhất 3 lần số tiền đầu tư trái phiếu ngân hàng nên ta có: \(1200 - x - y \ge 3x \Leftrightarrow 4x + y \le 1200\)
Bác An đầu tư không quá 200 triệu đồng cho trái phiếu doanh nghiệp nên \(y \le 200\)
Từ điều kiện của bài toán ta có số tiền bác An đầu tư trái phiếu phải thỏa mãn hệ:
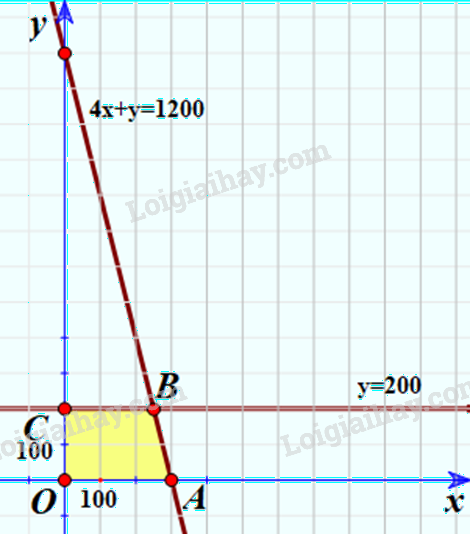
\(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\4x + y \le 1200\\y \le 200\end{array} \right.\)
Xác định miền nghiệm là miền tứ giác OABC với:
O(0;0); A(300;0); B(250;200); C(0;200).
Bước 2: Lợi nhuận thu được sau một năm là
\(\begin{array}{l}F\left( {x;y} \right) = \left( {1200 - x - y} \right).7\% + x.8\% + y.12\% \\ = 84 + 0,01x + 0,05y\end{array}\)
Ta cần tìm giá trị lớn nhất của F(x;y) khi (x;y) thỏa mãn hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\4x + y \le 1200\\y \le 200\end{array} \right.\)
Thay tọa độ các điểm O, A, B, C vào biểu thức F(x;y) ta được:
\(F\left( {0;0} \right) = 80\)
\(F\left( {300;0} \right) = 84 + 0,01.300 + 0,05.0 = 87\)
\(F\left( {250;200} \right) = 84 + 0,01.250 + 0,05.200 = 96,5\)
\(F\left( {0;200} \right) = 84 + 0,01.0 + 0,05.200 = 94\)
=> F đạt giá trị lớn nhất là 96,5 nếu x=250 và y=200.
Vậy bác An nên đầu tư 250 triệu đồng trái phiếu ngân hàng, 200 triệu trái phiếu doanh nghiệp và 750 trái phiếu chính phủ.
Bài 2.15 trang 32 SGK Toán 10 tập 1 – Kết nối tri thức yêu cầu học sinh giải quyết một bài toán liên quan đến vectơ, cụ thể là việc xác định mối quan hệ giữa các vectơ và tính toán độ dài của chúng. Để giải bài toán này một cách hiệu quả, chúng ta cần nắm vững các khái niệm cơ bản về vectơ, bao gồm:
Phân tích bài toán:
Trước khi bắt đầu giải bài toán, chúng ta cần đọc kỹ đề bài và xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Thông thường, đề bài sẽ cung cấp thông tin về các điểm, các vectơ hoặc các mối quan hệ giữa chúng. Dựa vào đó, chúng ta có thể vẽ một hình minh họa để dễ dàng hình dung bài toán.
Lời giải chi tiết:
Để giải bài 2.15 trang 32 SGK Toán 10 tập 1 – Kết nối tri thức, chúng ta sẽ thực hiện các bước sau:
Ví dụ minh họa:
Giả sử đề bài yêu cầu tính độ dài của vectơ AB, biết tọa độ của điểm A là (xA, yA) và tọa độ của điểm B là (xB, yB). Khi đó, chúng ta có thể sử dụng công thức tính độ dài của vectơ:
|AB| = √((xB - xA)2 + (yB - yA)2)
Lưu ý:
Trong quá trình giải bài toán, chúng ta cần chú ý đến việc sử dụng đúng các đơn vị đo lường và đảm bảo tính chính xác của các phép tính. Ngoài ra, chúng ta cũng nên kiểm tra lại kết quả để tránh sai sót.
Bài tập tương tự:
Để củng cố kiến thức về vectơ và các phép toán vectơ, các em học sinh có thể tự giải các bài tập tương tự trong SGK Toán 10 tập 1 – Kết nối tri thức hoặc các tài liệu tham khảo khác. Việc luyện tập thường xuyên sẽ giúp các em nắm vững kiến thức và tự tin giải các bài toán khó hơn.
Kết luận:
Bài 2.15 trang 32 SGK Toán 10 tập 1 – Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ và các phép toán vectơ. Bằng cách nắm vững các khái niệm cơ bản và áp dụng các công thức và quy tắc một cách linh hoạt, các em học sinh có thể giải quyết bài toán này một cách hiệu quả. Giaitoan.edu.vn hy vọng rằng lời giải chi tiết và dễ hiểu này sẽ giúp các em học sinh học Toán 10 hiệu quả hơn.
Các chủ đề liên quan:
Tài liệu tham khảo: