Bài 6.12 trang 16 SGK Toán 10 – Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 10. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 6.12 trang 16 SGK Toán 10 – Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Hai bạn An và Bình trao đổi với nhau. An nói: Tớ đọc ở một tài liệu thấy nói rằng cồng Trường Đại học Bách khoa Hà Nội (H.6.14) có dạng một parabol, khoảng cách giữa hai chân cổng là 8 m
Đề bài
Hai bạn An và Bình trao đổi với nhau.
An nói: Tớ đọc ở một tài liệu thấy nói rằng cồng Trường Đại học Bách khoa Hà Nội (H.6.14) có dạng một parabol, khoảng cách giữa hai chân cổng là 8 m và chiều cao của cổng tính từ một điểm trên mặt đất cách chân cổng 0,5 m là 2,93 m. Từ đó tớ tính ra được chiều cao của cổng parabol đó là 12 m
Sau một hồi suy nghĩ, Bình nói: Nếu dữ kiện như bạn nói, thì chiều cao của cổng parabol mà bạn tính ra ở trên là không chính xác.
Dựa vào thông tin mà An đọc được, em hãy tính chiều cao của cổng Trường Đại học Bách khoa Hà Nội để xem kết quả bạn An tính được có chính xác không nhé!

Phương pháp giải - Xem chi tiết
Cổng Trường Đại học Bách khoa Hà Nội có dạng là một parabol, giả sử parabol này có phương trình là \(y = a{x^2} + bx + c\) với a ≠ 0.
Chọn hệ trục tọa độ Oxy như hình vẽ với Oy là trục đối xứng của cổng parabol:
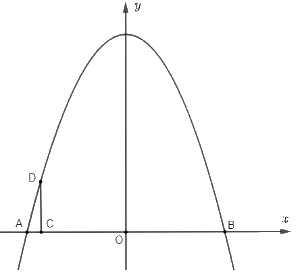
Tìm ra a,b,c. Tìm được tung độ đỉnh là chiều cao của cổng
Lời giải chi tiết
Theo bài ra ta có:
AB=8m => AO=OB=4m
AC=0,5m => OC=OA-AC=3,5m
=> Parabol đi qua điểm A(-4;0); B(4;0); C(-3,5; 2,93)
Do đó ta có các phương trình sau:
\(a.{( - 4)^2} + b( - 4) + c = 0 \Leftrightarrow 16a - 4b + c = 0\)
\(a{.4^2} + 4b + c = 0 \Leftrightarrow 16a + 4b + c = 0\)
\(a.{( - 3,5)^2} + b( - 3,5) + c = 2,93 \Leftrightarrow 12,25a - 3,5b + c = 2,93\)
Từ 3 phương trình trên, ta có: \(a = \frac{{ - 293}}{{375}};b = 0;c = \frac{{4688}}{{375}}\)
Tọa độ đỉnh là \(I\left( {0;\frac{{4688}}{{375}}} \right)\)
Vậy chiều cao của cổng parabol là \(\frac{{4688}}{{375}} \approx 12,5m\)
=> Kết quả của An tính ra không chính xác
Bài 6.12 trang 16 SGK Toán 10 – Kết nối tri thức thuộc chương 1: Vectơ trong mặt phẳng. Bài tập này tập trung vào việc áp dụng các tính chất của vectơ, đặc biệt là phép cộng, trừ vectơ và tích của một số với một vectơ để giải quyết các bài toán hình học.
Cho hình bình hành ABCD. Gọi M là trung điểm của BC. Gọi N là giao điểm của AM và BD. Chứng minh rằng: a) BN = 2ND; b) MN = 1/3 AM.
Để giải bài toán này, chúng ta sẽ sử dụng phương pháp vectơ. Việc biểu diễn các vectơ thông qua các vectơ cơ sở sẽ giúp chúng ta chứng minh các đẳng thức vectơ một cách dễ dàng.
Bài 6.12 trang 16 SGK Toán 10 – Kết nối tri thức là một bài tập điển hình về ứng dụng của vectơ trong hình học. Việc nắm vững các tính chất của vectơ và phương pháp giải bài tập sẽ giúp các em học sinh giải quyết các bài toán tương tự một cách hiệu quả.