Bài 1.26 trang 21 SGK Toán 10 tập 1 thuộc chương 1: Mệnh đề và tập hợp, là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về mệnh đề, tập hợp và các phép toán trên tập hợp. Bài tập này yêu cầu học sinh phải nắm vững định nghĩa, tính chất của các khái niệm cơ bản và áp dụng linh hoạt vào giải quyết vấn đề.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 1.26 trang 21 SGK Toán 10 tập 1 – Kết nối tri thức, giúp các em học sinh hiểu rõ bản chất của bài toán và tự tin giải các bài tập tương tự.
Xác định các tập hợp sau và biểu diễn chúng trên trục số.
Đề bài
Xác định các tập hợp sau và biểu diễn chúng trên trục số.
a) \(( - \infty ;1) \cap (0; + \infty )\)
b) \((4;7] \cup ( - 1;5)\)
c) \((4;7]\;{\rm{\backslash }}\;( - 3;5]\)
Phương pháp giải - Xem chi tiết
Biểu diễn các tập hợp trên trục số
Lời giải chi tiết
a) Ta có:
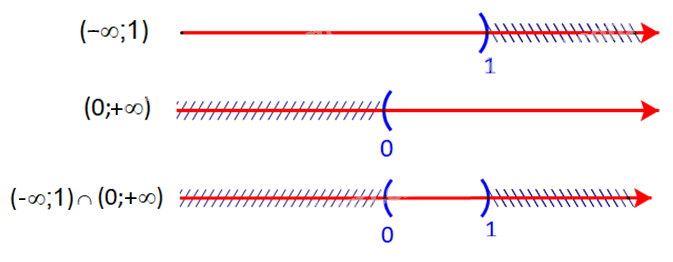
Giao của hai tập hợp là \(( - \infty ;1) \cap (0; + \infty ) = (0;1)\)
b) Ta có:
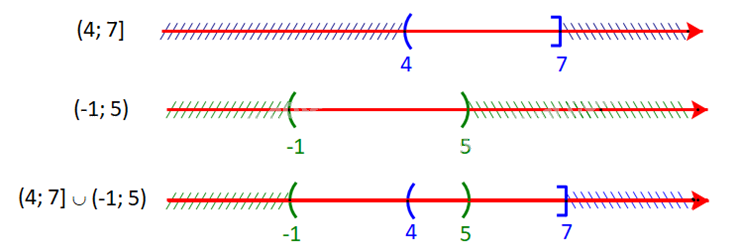
Hợp của hai tập hợp là \((4;7] \cup ( - 1;5) = ( - 1;7]\)
c) Ta có:
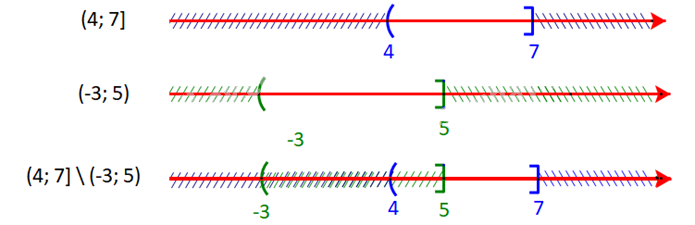
Hiệu của tập hợp \((4;7]\) và tập hợp \(( - 3;5]\) là \((4;7]\;{\rm{\backslash }}\;( - 3;5] = (5;7]\)
Bài 1.26 SGK Toán 10 tập 1 – Kết nối tri thức yêu cầu chúng ta xác định tính đúng sai của các mệnh đề liên quan đến tập hợp. Để giải bài này, trước hết cần nắm vững các khái niệm cơ bản về tập hợp, bao gồm:
Đề bài thường đưa ra các mệnh đề có dạng: “∀x ∈ A, P(x)”, “∃x ∈ A, P(x)”, hoặc các mệnh đề liên quan đến các phép toán trên tập hợp. Để xác định tính đúng sai của mệnh đề, ta cần:
(Nội dung lời giải chi tiết cho từng ý của bài 1.26 sẽ được trình bày tại đây. Ví dụ:)
a) Mệnh đề: “∀x ∈ ℝ, x2 > 0”
Mệnh đề này sai. Vì x = 0 thì x2 = 0, không lớn hơn 0. Do đó, không phải mọi x thuộc ℝ đều thỏa mãn x2 > 0.
b) Mệnh đề: “∃x ∈ ℤ, x2 = -1”
Mệnh đề này sai. Vì bình phương của một số nguyên luôn là một số không âm. Không có số nguyên nào bình phương bằng -1.
c) Mệnh đề: “∀x ∈ ℝ, x + 1 > x”
Mệnh đề này đúng. Vì cộng 1 vào một số thực bất kỳ luôn cho kết quả lớn hơn số thực ban đầu.
Để hiểu rõ hơn về cách giải các bài tập về mệnh đề và tập hợp, chúng ta cùng xem xét một số ví dụ minh họa:
Ví dụ 1: Cho A = {1, 2, 3} và B = {2, 4, 6}. Xác định A ∪ B và A ∩ B.
Lời giải:
Bài tập tương tự: Cho A = {a, b, c} và B = {b, d, e}. Xác định A ∪ B và A ∩ B.
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải bài 1.26 trang 21 SGK Toán 10 tập 1 – Kết nối tri thức và các bài tập tương tự. Chúc các em học tốt!