Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10 tập 2 Kết nối tri thức. Chúng tôi hiểu rằng việc tự học đôi khi gặp khó khăn, vì vậy chúng tôi luôn cố gắng mang đến những giải pháp tối ưu nhất.
Mục tiêu của chúng tôi là giúp bạn nắm vững kiến thức, tự tin giải quyết các bài toán và đạt kết quả cao trong học tập.
Một viên bi rơi tự do từ độ cao 19,6 m xuống mặt đất. Độ cao h (mét) so với mặt đất của viên bi trong khi rơi phụ thuộc vào thời gian t (giây) theo công thức:
Hàm số nào dưới đây là hàm số bậc hai?
A. \(y = {x^4} + 3{x^2} + 2\)
B.\(y = \frac{1}{{{x^2}}}\)
C.\(y = - 3{x^2} + 1\)
D.\(y = 3{\left( {\frac{1}{x}} \right)^2} + 3.\frac{1}{x} - 1\)\(\)
Phương pháp giải:
Hàm số bậc hai là hàm số có dạng: \(y = a{x^2} + bx + c(a \ne 0)\)
Lời giải chi tiết:
Hàm số \(y = - 3{x^2} + 1\) là hàm số bậc hai
Một viên bi rơi tự do từ độ cao 19,6 m xuống mặt đất. Độ cao h (mét) so với mặt đất của viên bi trong khi rơi phụ thuộc vào thời gian t (giây) theo công thức: \(h = 19,6 - 4,9{t^2};h,t \ge 0\).
a) Hỏi sau bao nhiêu giây kể từ khi rơi viên bi chạm đất?
b) Tìm tập xác định và tập giá trị của hàm số h.
Lời giải chi tiết:
a) Để viên bi chạm đất thì \(\begin{array}{l}h = 0 \Leftrightarrow 19,6 - 4,9{t^2} = 0\\ \Leftrightarrow 4,9{t^2} = 19,6 \Leftrightarrow {t^2} = 4\end{array}\)
Do \(t \ge 0\) nên t=2(s)
Vậy sau 2 giây thì viên bi chạm đất
b) Theo bài ra ta có: \(t \ge 0\) nên tập xác định của hàm số h là \(D = \left[ {0; + \infty } \right)\)
Mặt khác: \(4,9{t^2} \ge 0 \Rightarrow 19,6 - 4,9{t^2} \le 19,6\)
\( \Rightarrow 0 \le h \le 19,6\). Do đó tập giá trị của hàm số h là \(\left[ {0;19,6} \right]\)
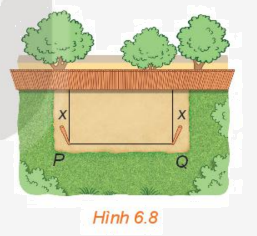
Xét bài toán rào vườn ở tình huống mở đầu. Gọi x mét \((0 < x < 10)\)là khoảng cách từ điểm cắm cọc đến bờ tường (H.6.8). Hãy tính theo x:
a) Độ dài cạnh PQ của mảnh đất.
b) Diện tích S(x) của mảnh đất được rào chắn.
Lời giải chi tiết:
a) Theo bài ra ta có: \(x + x + PQ = 20 \Rightarrow PQ = 20 - 2x\)(m)
b) Diện tích của mảnh đất được rào chắn là: \(\)\(x.PQ = x.(20 - 2x) = - 2{x^2} + 20x({m^2})\)
Cho hàm số \(y = (x - 1)(2 - 3x)\)
a) Hàm số đã cho có phải hàm số bậc hai không? Nếu có, hãy xác định các hệ số a, b, c của nó.
b) Thay dấu “?” bằng các số thích hợp để hoàn thành bảng giá trị sau của hàm số đã cho

Phương pháp giải:
Hàm số có dạng \(a{x^2} + bx + c(a \ne 0)\) là hàm số bậc hai
Lời giải chi tiết:
a) Ta có \((x - 1)(2 - 3x) = 2x - 3{x^2} - 2 + 3x = - 3{x^2} + 5x - 2\)
Do đó hàm y=(x-1)(2-3x) là hàm số bậc hai với \(a = - 3;b = 5;c = - 2\)
b) Thay các giá trị của x vào y=(x-1)(2-3x) ta có

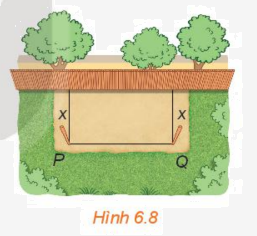
Xét bài toán rào vườn ở tình huống mở đầu. Gọi x mét \((0 < x < 10)\)là khoảng cách từ điểm cắm cọc đến bờ tường (H.6.8). Hãy tính theo x:
a) Độ dài cạnh PQ của mảnh đất.
b) Diện tích S(x) của mảnh đất được rào chắn.
Lời giải chi tiết:
a) Theo bài ra ta có: \(x + x + PQ = 20 \Rightarrow PQ = 20 - 2x\)(m)
b) Diện tích của mảnh đất được rào chắn là: \(\)\(x.PQ = x.(20 - 2x) = - 2{x^2} + 20x({m^2})\)
Hàm số nào dưới đây là hàm số bậc hai?
A. \(y = {x^4} + 3{x^2} + 2\)
B.\(y = \frac{1}{{{x^2}}}\)
C.\(y = - 3{x^2} + 1\)
D.\(y = 3{\left( {\frac{1}{x}} \right)^2} + 3.\frac{1}{x} - 1\)\(\)
Phương pháp giải:
Hàm số bậc hai là hàm số có dạng: \(y = a{x^2} + bx + c(a \ne 0)\)
Lời giải chi tiết:
Hàm số \(y = - 3{x^2} + 1\) là hàm số bậc hai
Cho hàm số \(y = (x - 1)(2 - 3x)\)
a) Hàm số đã cho có phải hàm số bậc hai không? Nếu có, hãy xác định các hệ số a, b, c của nó.
b) Thay dấu “?” bằng các số thích hợp để hoàn thành bảng giá trị sau của hàm số đã cho

Phương pháp giải:
Hàm số có dạng \(a{x^2} + bx + c(a \ne 0)\) là hàm số bậc hai
Lời giải chi tiết:
a) Ta có \((x - 1)(2 - 3x) = 2x - 3{x^2} - 2 + 3x = - 3{x^2} + 5x - 2\)
Do đó hàm y=(x-1)(2-3x) là hàm số bậc hai với \(a = - 3;b = 5;c = - 2\)
b) Thay các giá trị của x vào y=(x-1)(2-3x) ta có

Một viên bi rơi tự do từ độ cao 19,6 m xuống mặt đất. Độ cao h (mét) so với mặt đất của viên bi trong khi rơi phụ thuộc vào thời gian t (giây) theo công thức: \(h = 19,6 - 4,9{t^2};h,t \ge 0\).
a) Hỏi sau bao nhiêu giây kể từ khi rơi viên bi chạm đất?
b) Tìm tập xác định và tập giá trị của hàm số h.
Lời giải chi tiết:
a) Để viên bi chạm đất thì \(\begin{array}{l}h = 0 \Leftrightarrow 19,6 - 4,9{t^2} = 0\\ \Leftrightarrow 4,9{t^2} = 19,6 \Leftrightarrow {t^2} = 4\end{array}\)
Do \(t \ge 0\) nên t=2(s)
Vậy sau 2 giây thì viên bi chạm đất
b) Theo bài ra ta có: \(t \ge 0\) nên tập xác định của hàm số h là \(D = \left[ {0; + \infty } \right)\)
Mặt khác: \(4,9{t^2} \ge 0 \Rightarrow 19,6 - 4,9{t^2} \le 19,6\)
\( \Rightarrow 0 \le h \le 19,6\). Do đó tập giá trị của hàm số h là \(\left[ {0;19,6} \right]\)
Mục 1 của chương trình Toán 10 tập 2 Kết nối tri thức tập trung vào việc ôn tập và mở rộng kiến thức về vectơ. Các bài tập trang 11 và 12 SGK Toán 10 tập 2 yêu cầu học sinh vận dụng các khái niệm về vectơ, phép toán vectơ, và ứng dụng của vectơ trong hình học. Việc giải các bài tập này không chỉ giúp củng cố lý thuyết mà còn rèn luyện kỹ năng giải quyết vấn đề.
Bài 1 thường bao gồm các câu hỏi trắc nghiệm và bài tập tự luận về định nghĩa vectơ, các phép toán vectơ (cộng, trừ, nhân với một số), và các tính chất của phép toán vectơ. Để giải tốt bài 1, học sinh cần nắm vững các khái niệm cơ bản và các công thức liên quan.
Bài 2 thường tập trung vào việc sử dụng vectơ để chứng minh các tính chất hình học, giải các bài toán về hình học phẳng. Ví dụ, sử dụng vectơ để chứng minh hai đường thẳng song song, hai tam giác bằng nhau, hoặc tính diện tích hình bình hành.
Bài 3 thường là một bài tập tổng hợp, yêu cầu học sinh vận dụng kiến thức đã học để giải quyết một vấn đề phức tạp hơn. Bài tập này thường đòi hỏi học sinh phải có khả năng phân tích, tổng hợp và suy luận logic.
Ví dụ 1: Cho tam giác ABC, với A(1;2), B(3;4), C(5;6). Tính độ dài cạnh AB.
Giải: Sử dụng công thức tính độ dài vectơ: AB = √((3-1)² + (4-2)²) = √(2² + 2²) = √8 = 2√2
Ví dụ 2: Cho hai vectơ a = (1;2) và b = (3;4). Tính tích vô hướng của hai vectơ này.
Giải: Sử dụng công thức tính tích vô hướng: a.b = (1*3) + (2*4) = 3 + 8 = 11
Ngoài SGK Toán 10 tập 2 Kết nối tri thức, bạn có thể tham khảo thêm các tài liệu sau:
Việc giải các bài tập mục 1 trang 11, 12 SGK Toán 10 tập 2 Kết nối tri thức là một bước quan trọng trong quá trình học tập môn Toán. Hy vọng với những hướng dẫn và ví dụ minh họa trên, bạn sẽ tự tin giải quyết các bài tập và đạt kết quả tốt nhất. Chúc bạn học tập hiệu quả!