Bài 3.11 trang 43 SGK Toán 10 tập 1 thuộc chương 3: Hàm số và đồ thị. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai, điều kiện xác định và tập giá trị của hàm số để giải quyết.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Để tránh núi, giao thông hiện tại phải đi vòng như mô hình trong Hình 3.19. Để rút ngắn khoảng cách và tránh sạt lở núi, người ta dự định làm đường hầm xuyên núi, nối thẳng từ A tới D. Hỏi độ dài đường mới sẽ giảm bao nhiêu kilômét so với đường cũ?
Đề bài
Để tránh núi, giao thông hiện tại phải đi vòng như mô hình trong Hình 3.19. Để rút ngắn khoảng cách và tránh sạt lở núi, người ta dự định làm đường hầm xuyên núi, nối thẳng từ A tới D. Hỏi độ dài đường mới sẽ giảm bao nhiêu kilômét so với đường cũ?
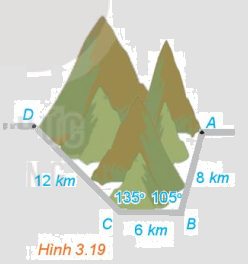
Phương pháp giải - Xem chi tiết
Bước 1: Tính AC: \(A{C^2} = B{C^2} + B{A^2} - 2.BC.BA.\cos ABC\)
Bước 2: Tính góc ACB, suy ra góc ACD.
Bước 3: Tính AD: \(A{D^2} = D{C^2} + C{A^2} - 2.DC.CA\cos ACD\)
Bước 4: Tính số kilomet giảm đi so với đường cũ.
Lời giải chi tiết
Bước 1:
Áp dụng định lí cos trong tam giác ABC ta có:
\(\begin{array}{l}A{C^2} = {6^2} + {8^2} - 2.6.8.\cos {105^o}\\ \Rightarrow AC \approx 11,1735\;(km)\end{array}\)
Bước 2:
Lại có: Theo định lí sin thì
\(\begin{array}{l}\frac{{AB}}{{\sin ACB}} = \frac{{AC}}{{\sin ABC}} \Rightarrow \sin ACB = \frac{{8.\sin {{105}^o}}}{{11,1735}}\\ \Rightarrow \widehat {ACB} \approx 44^o\\ \Rightarrow \widehat {ACD} = {135^o} - 44^o = 91^o\end{array}\)
Bước 3:
Áp dụng định lí cos trong tam giác ACD ta có:
\(\begin{array}{l}A{D^2} = {12^2} + 11,{1735^2} - 2.12.11,1735\cos 91^o\\ \Rightarrow AD \approx 16,5387\;(km)\end{array}\)
Bước 4:
Độ dài đường mới giảm số kilomet so với đường cũ là: \(12 + 6 + 8 - 16,5387 = 9,4613\;(km)\)
Bài 3.11 SGK Toán 10 tập 1 Kết nối tri thức yêu cầu chúng ta xét hàm số f(x) = -2x2 + 4x + 1 và thực hiện các yêu cầu sau:
Hàm số f(x) = -2x2 + 4x + 1 là một hàm số bậc hai. Đồ thị của hàm số là một parabol.
Như đã tính ở trên, tọa độ đỉnh của parabol là I(1; 3).
Trục đối xứng của parabol là đường thẳng x = x0 = 1.
Vì a = -2 < 0, hàm số nghịch biến trên khoảng (-∞; 1) và đồng biến trên khoảng (1; +∞).
Vì a = -2 < 0, parabol có giá trị lớn nhất tại đỉnh và không có giá trị nhỏ nhất.
Giá trị lớn nhất của hàm số là y0 = 3, đạt được khi x = 1.
Khi giải các bài tập về hàm số bậc hai, cần nắm vững các kiến thức sau:
Để củng cố kiến thức, các em có thể làm thêm các bài tập tương tự sau:
Bài 3.11 trang 43 SGK Toán 10 tập 1 – Kết nối tri thức là một bài tập quan trọng giúp học sinh hiểu rõ về hàm số bậc hai và các tính chất của nó. Hy vọng với lời giải chi tiết và hướng dẫn trên, các em học sinh sẽ tự tin hơn khi giải các bài tập tương tự.