Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10. Bài viết này sẽ hướng dẫn bạn cách giải bài 3.3 trang 37 SGK Toán 10 tập 1 – Kết nối tri thức một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn tự tin chinh phục môn Toán.
Chứng minh các hệ thức sau:
b) \(1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\quad (\alpha \ne {90^o})\)
Phương pháp giải:
Bước 1: Viết \(\tan \alpha \) dưới dạng \(\frac{{\sin \alpha }}{{\cos \alpha }}\;\;(\alpha \ne {90^o})\), thay vào vế trái.
Bước 2: Biến đổi vế trái bằng cách quy đồng, kết hợp với ý a) để suy ra vế phải.
Lời giải chi tiết:
Ta có: \(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}\;\;(\alpha \ne {90^o})\)
\( \Rightarrow 1 + {\tan ^2}\alpha = 1 + \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{{{{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} + \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }}\)
Mà theo ý a) ta có \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) với mọi góc \(\alpha \)
\( \Rightarrow 1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\) (đpcm)
c) \(1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }}\quad ({0^o} < \alpha < {180^o})\)
Phương pháp giải:
Bước 1: Viết \(\cot \alpha \) dưới dạng \(\frac{{\cos \alpha }}{{\sin \alpha }}\;\), thay vào vế trái.
Bước 2: Biến đổi vế trái bằng cách quy đồng, kết hợp với ý a) để suy ra vế phải.
Lời giải chi tiết:
Ta có: \(\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }}\;\;\;({0^o} < \alpha < {180^o})\)
\( \Rightarrow 1 + {\cot ^2}\alpha = 1 + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha }}{{{{\sin }^2}\alpha }} + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }}\)
Mà theo ý a) ta có \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) với mọi góc \(\alpha \)
\( \Rightarrow 1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }}\) (đpcm)
a) \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\).
Phương pháp giải:
Bước 1: Vẽ đường tròn lượng giác, lấy điểm M biểu diễn góc \(\alpha \) bất kì.
Bước 2: Xác định \(\sin \alpha ,\;\cos \alpha \)( tương ứng với tung độ và hoành độ của điểm M).
Bước 3: Suy ra đẳng thức cần chứng minh.
Lời giải chi tiết:
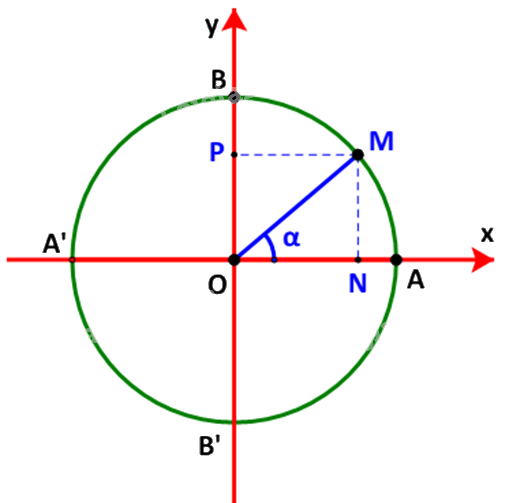
Gọi M(x;y) là điểm trên đường tròn đơn vị sao cho \(\widehat {xOM} = \alpha \). Gọi N, P tương ứng là hình chiếu vuông góc của M lên các trục Ox, Oy.
Ta có: \(\left\{ \begin{array}{l}x = \cos \alpha \\y = \sin \alpha \end{array} \right. \Rightarrow \left\{ \begin{array}{l}{\cos ^2}\alpha = {x^2}\\{\sin ^2}\alpha = {y^2}\end{array} \right.\)(1)
Mà \(\left\{ \begin{array}{l}\left| x \right| = ON\\\left| y \right| = OP = MN\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x^2} = {\left| x \right|^2} = O{N^2}\\{y^2} = {\left| y \right|^2} = M{N^2}\end{array} \right.\)(2)
Từ (1) và (2) suy ra \({\sin ^2}\alpha + {\cos ^2}\alpha = O{N^2} + M{N^2} = O{M^2}\) (do \(\Delta OMN\) vuông tại N)
\( \Rightarrow {\sin ^2}\alpha + {\cos ^2}\alpha = 1\) (vì OM = 1). (đpcm)
Chứng minh các hệ thức sau:
a) \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\).
b) \(1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\quad (\alpha \ne {90^o})\)
c) \(1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }}\quad ({0^o} < \alpha < {180^o})\)
a) \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\).
Phương pháp giải:
Bước 1: Vẽ đường tròn lượng giác, lấy điểm M biểu diễn góc \(\alpha \) bất kì.
Bước 2: Xác định \(\sin \alpha ,\;\cos \alpha \)( tương ứng với tung độ và hoành độ của điểm M).
Bước 3: Suy ra đẳng thức cần chứng minh.
Lời giải chi tiết:
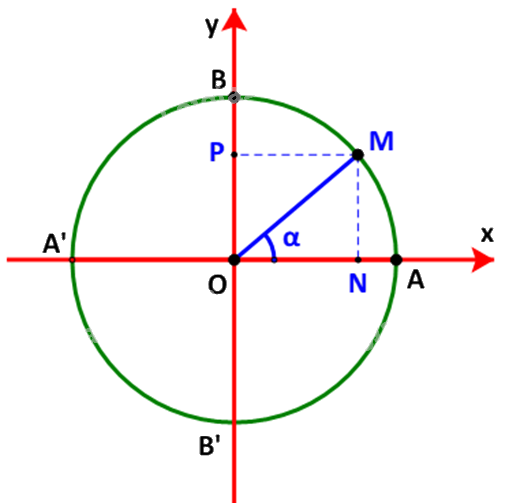
Gọi M(x;y) là điểm trên đường tròn đơn vị sao cho \(\widehat {xOM} = \alpha \). Gọi N, P tương ứng là hình chiếu vuông góc của M lên các trục Ox, Oy.
Ta có: \(\left\{ \begin{array}{l}x = \cos \alpha \\y = \sin \alpha \end{array} \right. \Rightarrow \left\{ \begin{array}{l}{\cos ^2}\alpha = {x^2}\\{\sin ^2}\alpha = {y^2}\end{array} \right.\)(1)
Mà \(\left\{ \begin{array}{l}\left| x \right| = ON\\\left| y \right| = OP = MN\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x^2} = {\left| x \right|^2} = O{N^2}\\{y^2} = {\left| y \right|^2} = M{N^2}\end{array} \right.\)(2)
Từ (1) và (2) suy ra \({\sin ^2}\alpha + {\cos ^2}\alpha = O{N^2} + M{N^2} = O{M^2}\) (do \(\Delta OMN\) vuông tại N)
\( \Rightarrow {\sin ^2}\alpha + {\cos ^2}\alpha = 1\) (vì OM = 1). (đpcm)
b) \(1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\quad (\alpha \ne {90^o})\)
Phương pháp giải:
Bước 1: Viết \(\tan \alpha \) dưới dạng \(\frac{{\sin \alpha }}{{\cos \alpha }}\;\;(\alpha \ne {90^o})\), thay vào vế trái.
Bước 2: Biến đổi vế trái bằng cách quy đồng, kết hợp với ý a) để suy ra vế phải.
Lời giải chi tiết:
Ta có: \(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}\;\;(\alpha \ne {90^o})\)
\( \Rightarrow 1 + {\tan ^2}\alpha = 1 + \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{{{{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} + \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }}\)
Mà theo ý a) ta có \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) với mọi góc \(\alpha \)
\( \Rightarrow 1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\) (đpcm)
c) \(1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }}\quad ({0^o} < \alpha < {180^o})\)
Phương pháp giải:
Bước 1: Viết \(\cot \alpha \) dưới dạng \(\frac{{\cos \alpha }}{{\sin \alpha }}\;\), thay vào vế trái.
Bước 2: Biến đổi vế trái bằng cách quy đồng, kết hợp với ý a) để suy ra vế phải.
Lời giải chi tiết:
Ta có: \(\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }}\;\;\;({0^o} < \alpha < {180^o})\)
\( \Rightarrow 1 + {\cot ^2}\alpha = 1 + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha }}{{{{\sin }^2}\alpha }} + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }}\)
Mà theo ý a) ta có \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) với mọi góc \(\alpha \)
\( \Rightarrow 1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }}\) (đpcm)
Bài 3.3 trang 37 SGK Toán 10 tập 1 – Kết nối tri thức thuộc chương 1: Mệnh đề và tập hợp. Bài tập này yêu cầu học sinh vận dụng kiến thức về tập hợp, các phép toán trên tập hợp (hợp, giao, hiệu, phần bù) để giải quyết các bài toán cụ thể. Việc nắm vững các khái niệm và tính chất của tập hợp là chìa khóa để giải quyết thành công bài tập này.
Bài tập 3.3 bao gồm một số câu hỏi nhỏ, yêu cầu học sinh:
Để giúp các bạn học sinh hiểu rõ hơn về cách giải bài tập này, chúng tôi xin trình bày lời giải chi tiết cho từng câu hỏi:
Đề bài: Cho A = {1; 2; 3; 4} và B = {3; 4; 5; 6}. Tìm A ∪ B.
Lời giải: A ∪ B là tập hợp chứa tất cả các phần tử thuộc A hoặc B (hoặc cả hai). Do đó, A ∪ B = {1; 2; 3; 4; 5; 6}.
Đề bài: Cho A = {1; 2; 3; 4} và B = {3; 4; 5; 6}. Tìm A ∩ B.
Lời giải: A ∩ B là tập hợp chứa tất cả các phần tử thuộc cả A và B. Do đó, A ∩ B = {3; 4}.
Đề bài: Cho A = {1; 2; 3; 4} và B = {3; 4; 5; 6}. Tìm A \ B.
Lời giải: A \ B là tập hợp chứa tất cả các phần tử thuộc A nhưng không thuộc B. Do đó, A \ B = {1; 2}.
Đề bài: Cho A = {1; 2; 3; 4} và B = {3; 4; 5; 6}. Tìm B \ A.
Lời giải: B \ A là tập hợp chứa tất cả các phần tử thuộc B nhưng không thuộc A. Do đó, B \ A = {5; 6}.
Trong thực tế, tập hợp được ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau. Ví dụ:
Hy vọng rằng, với lời giải chi tiết và những hướng dẫn trên, các bạn học sinh đã có thể tự tin giải bài 3.3 trang 37 SGK Toán 10 tập 1 – Kết nối tri thức. Chúc các bạn học tập tốt và đạt kết quả cao trong môn Toán!
| Tập hợp A | Tập hợp B | A ∪ B | A ∩ B | A \ B | B \ A |
|---|---|---|---|---|---|
| {1; 2; 3; 4} | {3; 4; 5; 6} | {1; 2; 3; 4; 5; 6} | {3; 4} | {1; 2} | {5; 6} |