Bài 6.19 trang 24 SGK Toán 10 – Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 10. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học để giải quyết vấn đề.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 6.19 trang 24 SGK Toán 10 – Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải bài tập.
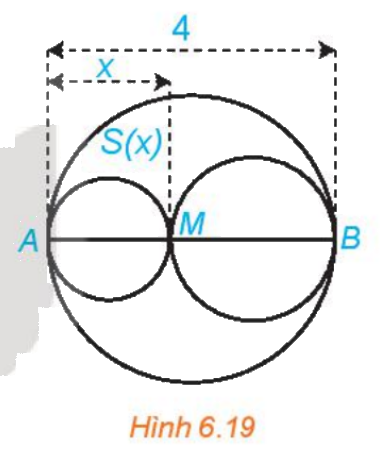
Xét đường tròn đường kính AB=4 và một điểm M di chuyển trên đoạn AB, đặt AM=x (H.6.19). Xét hai đường tròn đường kính AM và MB. Kí hiệu S(x) là diện tích phần hình phằng nằm trong hình tròn lớn và nằm ngoài hai hình tròn nhỏ.
Đề bài
Xét đường tròn đường kính AB=4 và một điểm M di chuyển trên đoạn AB, đặt AM=x (H.6.19). Xét hai đường tròn đường kính AM và MB. Kí hiệu S(x) là diện tích phần hình phằng nằm trong hình tròn lớn và nằm ngoài hai hình tròn nhỏ. Xác định các giá trị của x để diện tích S(x) không vượt quá một nửa tổng diện tích hai hình tròn nhỏ
Phương pháp giải - Xem chi tiết
Bước 1: Tính diện tích hình tròn đường kính AB, AM, MB theo x
Bước 2: Tính diện tích phần hình phằng nằm trong hình tròn lớn và nằm ngoài hai hình tròn nhỏ theo x
Bước 3: Lập bất phương trình từ dữ kiện bài toán
Lời giải chi tiết
Ta có: AM < AB nên \(0 < x < 4\).
Diện tích hình tròn đường kính AB là \({S_0} = \pi .{\left( {\frac{{AB}}{2}} \right)^2} = 4\pi \).
Diện tích hình tròn đường kính AM là \({S_1} = \pi .{\left( {\frac{{AM}}{2}} \right)^2} = \frac{{\pi .{x^2}}}{4}\).
Diện tích hình tròn đường kính MB là \({S_2} = \pi .{\left( {\frac{{MB}}{2}} \right)^2} = \pi .\frac{{{{\left( {4 - x} \right)}^2}}}{4}\).
Diện tích phần hình phẳng nằm trong hình tròn lớn và nằm ngoài hai hình tròn nhỏ là \(S(x) = {S_0} - {S_1} - {S_2} = 4\pi - \frac{{{x^2}}}{4}\pi - \frac{{{{\left( {4 - x} \right)}^2}}}{4}\pi = \frac{{ - {x^2} + 4x}}{2}\pi \).
Vì diện tich S(x) không vượt quá 1 nửa tổng diện tích hai hình tròn nhỏ nên:
\(S(x) \le \frac{1}{2}\left( {{S_1} + {S_2}} \right)\)
Khi đó : \(\frac{{ - {x^2} + 4x}}{2}\pi \le \frac{1}{2}.\frac{{{x^2} - 4x + 8}}{2}\pi \)
\( \Leftrightarrow - {x^2} + 4x \le \frac{{{x^2} - 4x + 8}}{2}\)
\( \Leftrightarrow - 2{x^2} + 8x \le {x^2} - 4x + 8\)
\( \Leftrightarrow 3{x^2} - 12x + 8 \ge 0\).
Xét tam thức \(3{x^2} - 12x + 8\) có \(\Delta ' = 12 > 0\) nên f(x) có 2 nghiệm phân biệt \({x_1} = \frac{{6 - 2\sqrt 3 }}{3};{x_2} = \frac{{6 + 2\sqrt 3 }}{3}\)
Mặt khác a=3>0, do đó ta có bảng xét dấu:
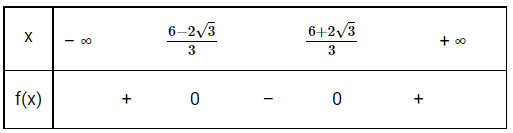
Do đó \(f(x) \ge 0\) với mọi \(x \in \left( { - \infty ;\frac{{6 - 2\sqrt 3 }}{3}} \right] \cup \left[ {\frac{{6 + 2\sqrt 3 }}{3}; + \infty } \right)\).
Mà 0 < x < 4 nên \(x \in \left( {0 ;\frac{{6 - 2\sqrt 3 }}{3}} \right] \cup \left[ {\frac{{6 + 2\sqrt 3 }}{3}; 4} \right)\).
Bài 6.19 trang 24 SGK Toán 10 – Kết nối tri thức là một bài toán thuộc chương trình học về vectơ trong không gian. Để giải bài toán này, học sinh cần nắm vững các kiến thức cơ bản về vectơ, bao gồm:
Bài toán 6.19 yêu cầu học sinh chứng minh một đẳng thức vectơ liên quan đến các điểm trong một hình bình hành. Cụ thể, cho hình bình hành ABCD, gọi O là giao điểm của hai đường chéo AC và BD. Chứng minh rằng: vectơ OA + vectơ OB + vectơ OC + vectơ OD = vectơ 0.
Để chứng minh đẳng thức vectơ trên, ta có thể sử dụng các tính chất của vectơ và hình bình hành. Ta biết rằng:
Áp dụng các tính chất trên, ta có:
Thay hai đẳng thức trên vào đẳng thức cần chứng minh, ta được:
vectơ OA + vectơ OB + vectơ OC + vectơ OD = vectơ OA + vectơ OB - vectơ OA - vectơ OB = vectơ 0
Vậy, đẳng thức vectơ OA + vectơ OB + vectơ OC + vectơ OD = vectơ 0 được chứng minh.
Bài toán 6.19 là một ví dụ điển hình về ứng dụng của vectơ trong hình học. Để hiểu sâu hơn về vectơ và các phép toán vectơ, học sinh có thể tham khảo thêm các bài tập tương tự, ví dụ:
Khi giải bài tập về vectơ, học sinh nên:
Bài 6.19 trang 24 SGK Toán 10 – Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về vectơ và rèn luyện kỹ năng giải bài tập. Hy vọng với lời giải chi tiết và dễ hiểu trên, các em học sinh sẽ tự tin hơn khi đối mặt với các bài toán tương tự.