Bài 1.25 trang 21 SGK Toán 10 tập 1 thuộc chương 1: Mệnh đề và tập hợp, là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về mệnh đề, tập hợp và các phép toán trên tập hợp. Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập này.
Chúng tôi luôn cố gắng cung cấp những lời giải chính xác, đầy đủ và dễ tiếp cận nhất, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Xác định các tập hợp sau
Đề bài
Cho \(A = [-2;3],\;\,B = (1; + \infty )\). Xác định các tập hợp sau:
\(\;A \cap B; B \backslash A \) và \({C_\mathbb{R}}B\)
Phương pháp giải - Xem chi tiết
Biểu diễn các tập hợp trên trục số
Lời giải chi tiết
Ta có:
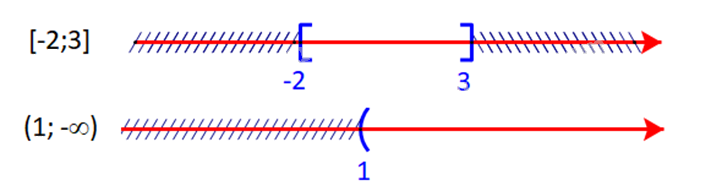
Giao của hai tập hợp là \([ - 2;3] \cap (1; + \infty ) = (1;3]\)
Hiệu của \(B \backslash A \) là \( (1; + \infty ) \backslash [ - 2;3] = (3; + \infty )\)
Phần bù của B trong \(\mathbb{R}\) là: \({C_\mathbb{R}}\;B = \mathbb{R}{\rm{\backslash }}\;(1; + \infty ) = ( - \infty ;1]\)
Bài 1.25 SGK Toán 10 tập 1 – Kết nối tri thức yêu cầu học sinh xác định tính đúng sai của các mệnh đề và thực hiện các phép toán trên tập hợp. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các khái niệm cơ bản về mệnh đề, tập hợp, và các phép toán như hợp, giao, hiệu, phần bù.
Bài tập 1.25 thường bao gồm các câu hỏi yêu cầu học sinh:
Giả sử bài 1.25 có các câu hỏi sau:
a) Giải: “Hôm nay là thứ Hai.” là một mệnh đề. Nó có thể đúng nếu hôm nay thực sự là thứ Hai, và sai nếu hôm nay không phải là thứ Hai.
b) Giải:
c) Giải: Để chứng minh đẳng thức A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C), ta có thể sử dụng sơ đồ Venn hoặc chứng minh bằng cách chỉ ra rằng mỗi phần tử thuộc tập hợp bên trái cũng thuộc tập hợp bên phải, và ngược lại.
Để củng cố kiến thức và kỹ năng giải bài tập về mệnh đề và tập hợp, các em có thể tham khảo thêm các bài tập tương tự trong SGK Toán 10 tập 1 – Kết nối tri thức, hoặc tìm kiếm trên các trang web học Toán online uy tín như giaitoan.edu.vn.
Bài 1.25 trang 21 SGK Toán 10 tập 1 – Kết nối tri thức là một bài tập quan trọng giúp học sinh nắm vững kiến thức cơ bản về mệnh đề và tập hợp. Bằng cách hiểu rõ các khái niệm, áp dụng các công thức và luyện tập thường xuyên, các em có thể tự tin giải quyết các bài tập tương tự và đạt kết quả tốt trong môn Toán.