Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 tập 1 Kết nối tri thức tại giaitoan.edu.vn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập trong SGK, giúp các em nắm vững kiến thức và tự tin hơn trong học tập.
Mục 2 của chương trình Toán 10 tập 1 tập trung vào các kiến thức cơ bản về tập hợp, các phép toán trên tập hợp và các ứng dụng của tập hợp trong thực tế.
Trong mặt phẳng tọa độ Oxy, cho u = (2; - 3), v = (4;1), a = (8; - 12 Trong mặt phẳng tọa độ Oxy, cho điểm M(x0, y0). Gọi P, Q tương ứng là hình chiếu vuông góc của M trên trục hoành Ox và trục tung Oy (H.4.35) Trong mặt phẳng tọa độ Oxy, cho các điểm M(x;y) và N(x’; y’) Trong mặt phẳng tọa độ Oxy, cho hai điểm A(2; 1), B(3; 3). Từ thông tin dự báo được đưa ra ở đầu bài học, hãy xác định tọa độ vị trí M của tâm bão tại thời điểm 9 giờ trong khoảng thời gian 12 giờ của dự báo.
Trong mặt phẳng tọa độ Oxy, cho điểm \(M({x_o};{y_o})\). Gọi P, Q tương ứng là hình chiếu vuông góc của M trên trục hoành Ox và trục tung Oy (H.4.35)
a) Trên trục Ox, điểm P biểu diễn số nào? Biểu thị \(\overrightarrow {OP} \) theo \(\overrightarrow i \) và tính độ dài của \(\overrightarrow {OP} \) theo \({x_o}\).
b) Trên trục Oy, điểm Q biểu diễn số nào? Biểu thị \(\overrightarrow {OQ} \) theo \(\overrightarrow j \) và tính độ dài của \(\overrightarrow {OQ} \) theo \({y_o}\).
c) Dựa vào hình chữ nhật OPMQ, tính độ dài của \(\overrightarrow {OM} \) theo \({x_o},{y_o}.\)
d) Biểu thị \(\overrightarrow {OM} \) theo các vectơ \(\overrightarrow i ,\;\overrightarrow j \).
Phương pháp giải:
a) P biểu diễn hoành độ của điểm M.
b) Q biểu diễn tung độ của điểm M.
c) Tính độ dài của \(\overrightarrow {OM} \) theo các cạnh của hình chữ nhật dựa vào định lí Pytago
d) Biểu thị \(\overrightarrow {OM} \) theo các vectơ \(\overrightarrow {OP} \), \(\overrightarrow {OQ} \) (quy tắc hình bình hành)
Lời giải chi tiết:
a) Vì P là hình chiếu vuông góc của M trên Ox nên điểm P biểu diễn hoành độ của điểm M là số \({x_o}\)
Ta có: vectơ \(\overrightarrow {OP} \) cùng phương, cùng hướng với \(\overrightarrow i \) và \(\left| {\overrightarrow {OP} } \right| = {x_o} = {x_o}.\left| {\overrightarrow i } \right|\)
\( \Rightarrow \overrightarrow {OP} = {x_o}.\;\overrightarrow i \).
b) Vì Q là hình chiếu vuông góc của M trên Oy nên điểm Q biểu diễn tung độ của điểm M là số \({y_o}\)
Ta có: vectơ \(\overrightarrow {OQ} \) cùng phương, cùng hướng với \(\overrightarrow j \) và \(\left| {\overrightarrow {OQ} } \right| = {y_o} = {y_o}.\left| {\overrightarrow j } \right|\)
\( \Rightarrow \overrightarrow {OQ} = {y_o}.\;\overrightarrow j \).
c) Ta có: \(\overrightarrow {OM} = OM\).
Mà \(O{M^2} = O{P^2} + M{P^2} = O{P^2} + O{Q^2} = {x_o}^2 + {y_o}^2\)
\( \Rightarrow \left| {\overrightarrow {OM} } \right| = \sqrt {{x_o}^2 + {y_o}^2} \)
d) Ta có: Tứ giác OPMQ là hình chữ nhật, cũng là hình bình hành nên \(\overrightarrow {OM} = \overrightarrow {OP} + \overrightarrow {OQ} \)
\( \Rightarrow \overrightarrow {OM} = {x_o}.\;\overrightarrow i + {y_o}.\;\overrightarrow j \)
Trong mặt phẳng tọa độ Oxy, cho \(\overrightarrow u = (2; - 3),\;\overrightarrow v = (4;1),\;\overrightarrow a = (8; - 12)\)
a) Hãy biểu thị mỗi vectơ \(\overrightarrow u ,\;\overrightarrow v ,\;\overrightarrow a \) theo các vectơ \(\overrightarrow i ,\;\overrightarrow j \)
b) Tìm tọa độ của các vectơ \(\overrightarrow u + \;\overrightarrow v ,\;4.\;\overrightarrow u \)
c) Tìm mối liên hệ giữa hai vectơ \(\overrightarrow u ,\;\overrightarrow a \)
Phương pháp giải:
a) Vectơ \(\overrightarrow a \) có tọa độ (x;y) thì \(\overrightarrow a = x.\;\overrightarrow i + y.\;\overrightarrow j \)
b)
Bước 1: Tính \(\overrightarrow u + \;\overrightarrow v ,\;4.\;\overrightarrow u \) theo các vectơ \(\overrightarrow i ,\;\overrightarrow j \)
Bước 2: Suy ra tọa độ của các vectơ \(\overrightarrow u + \;\overrightarrow v ,\;4.\;\overrightarrow u \)
c)
Quan sát biểu thị theo các vectơ \(\overrightarrow i ,\;\overrightarrow j \) của các vectơ \(\overrightarrow u ,\;\overrightarrow a \) để suy ra mối liên hệ.
Lời giải chi tiết:
a) Ta có: \(\overrightarrow u = (2; - 3)\)
\( \Rightarrow \overrightarrow u = 2.\;\overrightarrow i + \left( { - 3} \right).\;\overrightarrow j \)
Tương tự ta có: \(\overrightarrow v = (4;1),\;\overrightarrow a = (8; - 12)\)
\( \Rightarrow \overrightarrow v = 4.\;\overrightarrow i + 1.\;\overrightarrow j ;\;\;\overrightarrow a = 8.\;\overrightarrow i + \left( { - 12} \right).\;\overrightarrow j \)
b) Ta có: \(\left\{ \begin{array}{l}\overrightarrow u = 2.\;\overrightarrow i + \left( { - 3} \right).\;\overrightarrow j \\\overrightarrow v = 4.\;\overrightarrow i + 1.\;\overrightarrow j \end{array} \right.\)(theo câu a)
\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}\overrightarrow u + \;\overrightarrow v = \left( {2.\;\overrightarrow i + \left( { - 3} \right).\;\overrightarrow j } \right) + \left( {4.\;\overrightarrow i + 1.\;\overrightarrow j } \right)\\4.\;\overrightarrow u = 4\left( {2.\;\overrightarrow i + \left( { - 3} \right).\;\overrightarrow j } \right)\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow u + \;\overrightarrow v = \left( {2.\;\overrightarrow i + 4.\;\overrightarrow i } \right) + \left( {\left( { - 3} \right).\;\overrightarrow j + 1.\;\overrightarrow j } \right)\\4.\;\overrightarrow u = 4.2.\;\overrightarrow i + 4.\left( { - 3} \right).\;\overrightarrow j \end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow u + \;\overrightarrow v = 6.\;\overrightarrow i + \left( { - 2} \right).\;\overrightarrow j \\4.\;\overrightarrow u = 8.\;\overrightarrow i + \left( { - 12} \right).\;\overrightarrow j \end{array} \right.\end{array}\)
c) Vì \(\left\{ \begin{array}{l}4.\;\overrightarrow u = 8.\;\overrightarrow i + \left( { - 12} \right).\;\overrightarrow j \\\overrightarrow a = 8.\;\overrightarrow i + \left( { - 12} \right).\;\overrightarrow j \end{array} \right.\) nên ta suy ra \(4.\;\overrightarrow u = \overrightarrow a \)
Trong mặt phẳng tọa độ Oxy, cho các điểm M(x;y) và N(x’; y’)
a) Tìm tọa độ của các vectơ \(\overrightarrow {OM} ,\;\overrightarrow {ON} \).
b) Biểu thị vectơ \(\overrightarrow {MN} \) theo các vectơ \(\overrightarrow {OM} ,\;\overrightarrow {ON} \) và tọa độ của \(\overrightarrow {MN} \).
c) Tìm độ dài của vectơ \(\overrightarrow {MN} \)
Phương pháp giải:
a) Tọa độ của vectơ \(\overrightarrow {OM} ,\;\overrightarrow {ON} \) chính là tọa độ của M, N
b) Biểu thị vectơ \(\overrightarrow {MN} \) theo các vectơ \(\overrightarrow {OM} ,\;\overrightarrow {ON} \) bằng quy tắc hiệu.
Tìm tọa độ của \(\overrightarrow {MN} \) dựa vào biểu thị theo hiệu ở trên và tọa độ của vectơ \(\overrightarrow {OM} ,\;\overrightarrow {ON} \) đã biết.
c) Độ dài của vectơ \(\overrightarrow {MN} (a;b)\) là \(\left| {\overrightarrow {MN} } \right| = \sqrt {{a^2} + {b^2}} \)
Lời giải chi tiết:
a) Vì điểm M có tọa độ (x; y) nên vectơ \(\overrightarrow {OM} \) có tọa độ (x; y).
Và điểm N có tọa độ (x’; y’) nên vectơ \(\overrightarrow {ON} \) có tọa độ (x’; y’).
b) Ta có: \(\overrightarrow {MN} = \overrightarrow {ON} - \overrightarrow {OM} \) (quy tắc hiệu)
Mà \(\overrightarrow {OM} \) có tọa độ (x; y); \(\overrightarrow {ON} \) có tọa độ (x’; y’).
\( \Rightarrow \overrightarrow {MN} = \left( {x';y'} \right) - \left( {x;y} \right) = \left( {x' - x;y' - y} \right)\)
c) Vì \(\overrightarrow {MN} \) có tọa độ \(\left( {x' - x;y' - y} \right)\) nên \(\left| {\overrightarrow {MN} } \right| = \sqrt {{{\left( {x' - x} \right)}^2} + {{\left( {y' - y} \right)}^2}} \)
Trong mặt phẳng tọa độ Oxy, cho hai điểm A(2; 1), B(3; 3).
a) Các điểm O, A, B có thẳng hàng hay không?
b) Tìm điểm M(x; y) để OABM là một hình hành.
Phương pháp giải:
a) Các điểm O, A, B thẳng hàng khi và chỉ khi hai vectơ \(\overrightarrow {OA} ,\;\overrightarrow {OB} \) cùng phương
b) OABM là một hình hành khi và chỉ khi \(\overrightarrow {OA} = \overrightarrow {MB} \)
Lời giải chi tiết:
a) Ta có: \(\overrightarrow {OA} = \left( {2;1} \right)\) ( do A(2; 1)) và \(\overrightarrow {OB} = \left( {3;3} \right)\) (do B (3; 3)).
Hai vectơ này không cùng phương (vì \(\frac{2}{3} \ne \frac{1}{3}\)).
Do đó các điểm O, A, B không cùng nằm trên một đường thẳng.
Vậy chúng không thẳng hàng.
b) Các điểm O, A, B không thẳng hàng nên OABM là một hình hành khi và chỉ khi \(\overrightarrow {OA} = \overrightarrow {MB} \).
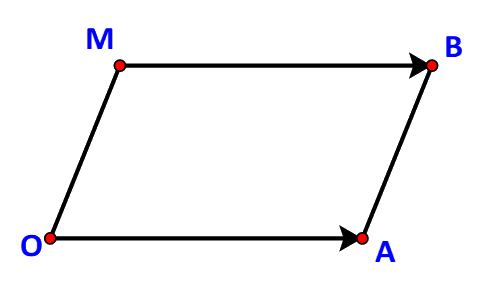
Do \(\overrightarrow {OA} = \left( {2;1} \right),\quad \overrightarrow {MB} = \left( {3 - x;3 - y} \right)\) nên
\(\overrightarrow {OA} = \overrightarrow {MB} \Leftrightarrow \left\{ \begin{array}{l}2 = 3 - x\\1 = 3 - y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 2\end{array} \right.\)
Vậy điểm cần tìm là M (1; 2).
Từ thông tin dự báo được đưa ra ở đầu bài học, hãy xác định tọa độ vị trí M của tâm bão tại thời điểm 9 giờ trong khoảng thời gian 12 giờ của dự báo.

Lời giải chi tiết:
Gọi tọa độ điểm M là (x; y)
Theo dự báo, tại thời điểm 9 giờ, tâm bão đã đi được \(\frac{9}{{12}} = \frac{3}{4}\) khoảng cách từ A tới B.
Hay \(AM = \frac{3}{4}.AB \Rightarrow \overrightarrow {AM} = \frac{3}{4}.\overrightarrow {AB} \)(*)
Mà \(\overrightarrow {AM} = \left( {x - 13,8;y - 108,3} \right),\;\)\(\,\overrightarrow {AB} = \left( {14,1 - 13,8;106,3 - 108,3} \right) = \left( {0,3; - 2} \right)\)
Do đó \((*) \Leftrightarrow \left\{ \begin{array}{l}x - 13,8 = \frac{3}{4}.0,3\\y - 108,3 = \frac{3}{4}.\left( { - 2} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 14,025\\y = 106,8\end{array} \right.\)
Vậy tọa độ điểm M là (14,025; 106,8)
Trong mặt phẳng tọa độ Oxy, cho \(\overrightarrow u = (2; - 3),\;\overrightarrow v = (4;1),\;\overrightarrow a = (8; - 12)\)
a) Hãy biểu thị mỗi vectơ \(\overrightarrow u ,\;\overrightarrow v ,\;\overrightarrow a \) theo các vectơ \(\overrightarrow i ,\;\overrightarrow j \)
b) Tìm tọa độ của các vectơ \(\overrightarrow u + \;\overrightarrow v ,\;4.\;\overrightarrow u \)
c) Tìm mối liên hệ giữa hai vectơ \(\overrightarrow u ,\;\overrightarrow a \)
Phương pháp giải:
a) Vectơ \(\overrightarrow a \) có tọa độ (x;y) thì \(\overrightarrow a = x.\;\overrightarrow i + y.\;\overrightarrow j \)
b)
Bước 1: Tính \(\overrightarrow u + \;\overrightarrow v ,\;4.\;\overrightarrow u \) theo các vectơ \(\overrightarrow i ,\;\overrightarrow j \)
Bước 2: Suy ra tọa độ của các vectơ \(\overrightarrow u + \;\overrightarrow v ,\;4.\;\overrightarrow u \)
c)
Quan sát biểu thị theo các vectơ \(\overrightarrow i ,\;\overrightarrow j \) của các vectơ \(\overrightarrow u ,\;\overrightarrow a \) để suy ra mối liên hệ.
Lời giải chi tiết:
a) Ta có: \(\overrightarrow u = (2; - 3)\)
\( \Rightarrow \overrightarrow u = 2.\;\overrightarrow i + \left( { - 3} \right).\;\overrightarrow j \)
Tương tự ta có: \(\overrightarrow v = (4;1),\;\overrightarrow a = (8; - 12)\)
\( \Rightarrow \overrightarrow v = 4.\;\overrightarrow i + 1.\;\overrightarrow j ;\;\;\overrightarrow a = 8.\;\overrightarrow i + \left( { - 12} \right).\;\overrightarrow j \)
b) Ta có: \(\left\{ \begin{array}{l}\overrightarrow u = 2.\;\overrightarrow i + \left( { - 3} \right).\;\overrightarrow j \\\overrightarrow v = 4.\;\overrightarrow i + 1.\;\overrightarrow j \end{array} \right.\)(theo câu a)
\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}\overrightarrow u + \;\overrightarrow v = \left( {2.\;\overrightarrow i + \left( { - 3} \right).\;\overrightarrow j } \right) + \left( {4.\;\overrightarrow i + 1.\;\overrightarrow j } \right)\\4.\;\overrightarrow u = 4\left( {2.\;\overrightarrow i + \left( { - 3} \right).\;\overrightarrow j } \right)\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow u + \;\overrightarrow v = \left( {2.\;\overrightarrow i + 4.\;\overrightarrow i } \right) + \left( {\left( { - 3} \right).\;\overrightarrow j + 1.\;\overrightarrow j } \right)\\4.\;\overrightarrow u = 4.2.\;\overrightarrow i + 4.\left( { - 3} \right).\;\overrightarrow j \end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow u + \;\overrightarrow v = 6.\;\overrightarrow i + \left( { - 2} \right).\;\overrightarrow j \\4.\;\overrightarrow u = 8.\;\overrightarrow i + \left( { - 12} \right).\;\overrightarrow j \end{array} \right.\end{array}\)
c) Vì \(\left\{ \begin{array}{l}4.\;\overrightarrow u = 8.\;\overrightarrow i + \left( { - 12} \right).\;\overrightarrow j \\\overrightarrow a = 8.\;\overrightarrow i + \left( { - 12} \right).\;\overrightarrow j \end{array} \right.\) nên ta suy ra \(4.\;\overrightarrow u = \overrightarrow a \)
Trong mặt phẳng tọa độ Oxy, cho điểm \(M({x_o};{y_o})\). Gọi P, Q tương ứng là hình chiếu vuông góc của M trên trục hoành Ox và trục tung Oy (H.4.35)
a) Trên trục Ox, điểm P biểu diễn số nào? Biểu thị \(\overrightarrow {OP} \) theo \(\overrightarrow i \) và tính độ dài của \(\overrightarrow {OP} \) theo \({x_o}\).
b) Trên trục Oy, điểm Q biểu diễn số nào? Biểu thị \(\overrightarrow {OQ} \) theo \(\overrightarrow j \) và tính độ dài của \(\overrightarrow {OQ} \) theo \({y_o}\).
c) Dựa vào hình chữ nhật OPMQ, tính độ dài của \(\overrightarrow {OM} \) theo \({x_o},{y_o}.\)
d) Biểu thị \(\overrightarrow {OM} \) theo các vectơ \(\overrightarrow i ,\;\overrightarrow j \).
Phương pháp giải:
a) P biểu diễn hoành độ của điểm M.
b) Q biểu diễn tung độ của điểm M.
c) Tính độ dài của \(\overrightarrow {OM} \) theo các cạnh của hình chữ nhật dựa vào định lí Pytago
d) Biểu thị \(\overrightarrow {OM} \) theo các vectơ \(\overrightarrow {OP} \), \(\overrightarrow {OQ} \) (quy tắc hình bình hành)
Lời giải chi tiết:
a) Vì P là hình chiếu vuông góc của M trên Ox nên điểm P biểu diễn hoành độ của điểm M là số \({x_o}\)
Ta có: vectơ \(\overrightarrow {OP} \) cùng phương, cùng hướng với \(\overrightarrow i \) và \(\left| {\overrightarrow {OP} } \right| = {x_o} = {x_o}.\left| {\overrightarrow i } \right|\)
\( \Rightarrow \overrightarrow {OP} = {x_o}.\;\overrightarrow i \).
b) Vì Q là hình chiếu vuông góc của M trên Oy nên điểm Q biểu diễn tung độ của điểm M là số \({y_o}\)
Ta có: vectơ \(\overrightarrow {OQ} \) cùng phương, cùng hướng với \(\overrightarrow j \) và \(\left| {\overrightarrow {OQ} } \right| = {y_o} = {y_o}.\left| {\overrightarrow j } \right|\)
\( \Rightarrow \overrightarrow {OQ} = {y_o}.\;\overrightarrow j \).
c) Ta có: \(\overrightarrow {OM} = OM\).
Mà \(O{M^2} = O{P^2} + M{P^2} = O{P^2} + O{Q^2} = {x_o}^2 + {y_o}^2\)
\( \Rightarrow \left| {\overrightarrow {OM} } \right| = \sqrt {{x_o}^2 + {y_o}^2} \)
d) Ta có: Tứ giác OPMQ là hình chữ nhật, cũng là hình bình hành nên \(\overrightarrow {OM} = \overrightarrow {OP} + \overrightarrow {OQ} \)
\( \Rightarrow \overrightarrow {OM} = {x_o}.\;\overrightarrow i + {y_o}.\;\overrightarrow j \)
Trong mặt phẳng tọa độ Oxy, cho các điểm M(x;y) và N(x’; y’)
a) Tìm tọa độ của các vectơ \(\overrightarrow {OM} ,\;\overrightarrow {ON} \).
b) Biểu thị vectơ \(\overrightarrow {MN} \) theo các vectơ \(\overrightarrow {OM} ,\;\overrightarrow {ON} \) và tọa độ của \(\overrightarrow {MN} \).
c) Tìm độ dài của vectơ \(\overrightarrow {MN} \)
Phương pháp giải:
a) Tọa độ của vectơ \(\overrightarrow {OM} ,\;\overrightarrow {ON} \) chính là tọa độ của M, N
b) Biểu thị vectơ \(\overrightarrow {MN} \) theo các vectơ \(\overrightarrow {OM} ,\;\overrightarrow {ON} \) bằng quy tắc hiệu.
Tìm tọa độ của \(\overrightarrow {MN} \) dựa vào biểu thị theo hiệu ở trên và tọa độ của vectơ \(\overrightarrow {OM} ,\;\overrightarrow {ON} \) đã biết.
c) Độ dài của vectơ \(\overrightarrow {MN} (a;b)\) là \(\left| {\overrightarrow {MN} } \right| = \sqrt {{a^2} + {b^2}} \)
Lời giải chi tiết:
a) Vì điểm M có tọa độ (x; y) nên vectơ \(\overrightarrow {OM} \) có tọa độ (x; y).
Và điểm N có tọa độ (x’; y’) nên vectơ \(\overrightarrow {ON} \) có tọa độ (x’; y’).
b) Ta có: \(\overrightarrow {MN} = \overrightarrow {ON} - \overrightarrow {OM} \) (quy tắc hiệu)
Mà \(\overrightarrow {OM} \) có tọa độ (x; y); \(\overrightarrow {ON} \) có tọa độ (x’; y’).
\( \Rightarrow \overrightarrow {MN} = \left( {x';y'} \right) - \left( {x;y} \right) = \left( {x' - x;y' - y} \right)\)
c) Vì \(\overrightarrow {MN} \) có tọa độ \(\left( {x' - x;y' - y} \right)\) nên \(\left| {\overrightarrow {MN} } \right| = \sqrt {{{\left( {x' - x} \right)}^2} + {{\left( {y' - y} \right)}^2}} \)
Trong mặt phẳng tọa độ Oxy, cho hai điểm A(2; 1), B(3; 3).
a) Các điểm O, A, B có thẳng hàng hay không?
b) Tìm điểm M(x; y) để OABM là một hình hành.
Phương pháp giải:
a) Các điểm O, A, B thẳng hàng khi và chỉ khi hai vectơ \(\overrightarrow {OA} ,\;\overrightarrow {OB} \) cùng phương
b) OABM là một hình hành khi và chỉ khi \(\overrightarrow {OA} = \overrightarrow {MB} \)
Lời giải chi tiết:
a) Ta có: \(\overrightarrow {OA} = \left( {2;1} \right)\) ( do A(2; 1)) và \(\overrightarrow {OB} = \left( {3;3} \right)\) (do B (3; 3)).
Hai vectơ này không cùng phương (vì \(\frac{2}{3} \ne \frac{1}{3}\)).
Do đó các điểm O, A, B không cùng nằm trên một đường thẳng.
Vậy chúng không thẳng hàng.
b) Các điểm O, A, B không thẳng hàng nên OABM là một hình hành khi và chỉ khi \(\overrightarrow {OA} = \overrightarrow {MB} \).
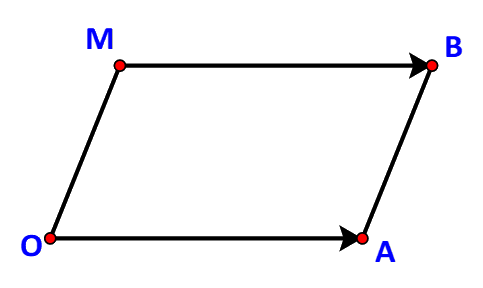
Do \(\overrightarrow {OA} = \left( {2;1} \right),\quad \overrightarrow {MB} = \left( {3 - x;3 - y} \right)\) nên
\(\overrightarrow {OA} = \overrightarrow {MB} \Leftrightarrow \left\{ \begin{array}{l}2 = 3 - x\\1 = 3 - y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 2\end{array} \right.\)
Vậy điểm cần tìm là M (1; 2).
Từ thông tin dự báo được đưa ra ở đầu bài học, hãy xác định tọa độ vị trí M của tâm bão tại thời điểm 9 giờ trong khoảng thời gian 12 giờ của dự báo.

Lời giải chi tiết:
Gọi tọa độ điểm M là (x; y)
Theo dự báo, tại thời điểm 9 giờ, tâm bão đã đi được \(\frac{9}{{12}} = \frac{3}{4}\) khoảng cách từ A tới B.
Hay \(AM = \frac{3}{4}.AB \Rightarrow \overrightarrow {AM} = \frac{3}{4}.\overrightarrow {AB} \)(*)
Mà \(\overrightarrow {AM} = \left( {x - 13,8;y - 108,3} \right),\;\)\(\,\overrightarrow {AB} = \left( {14,1 - 13,8;106,3 - 108,3} \right) = \left( {0,3; - 2} \right)\)
Do đó \((*) \Leftrightarrow \left\{ \begin{array}{l}x - 13,8 = \frac{3}{4}.0,3\\y - 108,3 = \frac{3}{4}.\left( { - 2} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 14,025\\y = 106,8\end{array} \right.\)
Vậy tọa độ điểm M là (14,025; 106,8)
Mục 2 trong SGK Toán 10 tập 1 Kết nối tri thức là nền tảng quan trọng để học sinh làm quen với các khái niệm cơ bản của tập hợp, một trong những khái niệm cốt lõi của toán học. Việc nắm vững kiến thức này sẽ giúp các em dễ dàng tiếp thu các kiến thức nâng cao hơn trong các chương trình học tiếp theo.
Mục 2 bao gồm các nội dung chính sau:
Trang 61 tập trung vào việc củng cố kiến thức về khái niệm tập hợp và cách biểu diễn tập hợp. Các bài tập thường yêu cầu học sinh:
Ví dụ, bài tập 1 yêu cầu liệt kê các phần tử của tập hợp A các số tự nhiên chẵn nhỏ hơn 10. Lời giải là A = {0, 2, 4, 6, 8}.
Trang 62 giới thiệu về các loại tập hợp như tập hợp rỗng, tập hợp con và tập hợp bằng nhau. Các bài tập thường yêu cầu học sinh:
Ví dụ, bài tập 2 yêu cầu xác định xem tập hợp B = {1, 2, 3} có phải là tập hợp con của tập hợp C = {1, 2, 3, 4, 5} hay không. Lời giải là B là tập hợp con của C.
Trang 63 và 64 tập trung vào các phép toán trên tập hợp như hợp, giao, hiệu và phần bù. Các bài tập thường yêu cầu học sinh:
Ví dụ, bài tập 3 yêu cầu tìm hợp của hai tập hợp D = {1, 2, 3} và E = {3, 4, 5}. Lời giải là D ∪ E = {1, 2, 3, 4, 5}.
Để học tốt Mục 2, các em nên:
Mục 2 là một phần quan trọng trong chương trình Toán 10 tập 1 Kết nối tri thức. Việc nắm vững kiến thức và kỹ năng trong mục này sẽ giúp các em học tốt các chương trình học tiếp theo. Chúc các em học tập tốt!