Bài 3.10 trang 43 SGK Toán 10 tập 1 thuộc chương 1: Mệnh đề và tập hợp. Bài tập này yêu cầu học sinh vận dụng kiến thức về tập hợp, các phép toán trên tập hợp để giải quyết các bài toán cụ thể.
Giaitoan.edu.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Từ bãi biển Vũng Chùa, Quảng Bình, ta có thể ngắm được Đảo Yến. Hãy đề xuất một các xác định bề rộng của hòn đảo (theo chiều ta ngắm được).
Đề bài
Từ bãi biển Vũng Chùa, Quảng Bình, ta có thể ngắm được Đảo Yến. Hãy đề xuất một các xác định bề rộng của hòn đảo (theo chiều ta ngắm được).

Lời giải chi tiết
Bước 1:
Đánh dấu vị trí quan sát tại điểm A, chiều rộng của hòn đảo kí hiệu là đoạn BC.
Gọi H là hình chiếu của A trên BC.
Trên tia đối của tia AH, lấy điểm M, ghi lại khoảng cách AM = a.
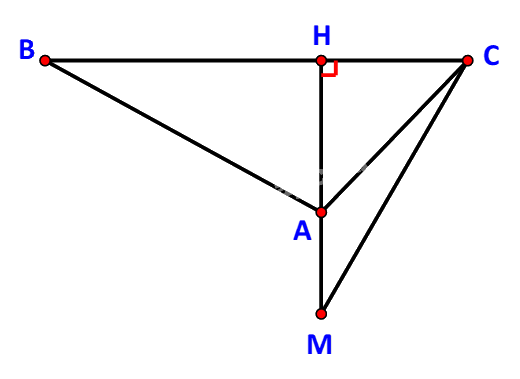
Bước 2:
Tại A, quan sát để xác định các góc \(\widehat {BAC} = \alpha ,\;\widehat {HAC} = \beta \).
Tiếp tục quan sát tại M, xác định góc \(\widehat {HMC} = \gamma \).
Bước 3: Giải tam giác AMC, tính AC.
AM = a, \(\widehat {AMC} = \widehat {HMC} = \gamma \) và \(\widehat {MAC} = {180^o} - \beta \)
\( \Rightarrow \widehat {ACM} = {180^o} - \gamma - \left( {{{180}^o} - \beta } \right) = \beta - \gamma \)
Áp dụng định định lí sin trong tam giác AMC ta có:
\(\frac{{AC}}{{\sin AMC}} = \frac{{AM}}{{\sin ACM}} \Rightarrow AC = \sin \gamma .\frac{a}{{\sin \left( {\beta - \gamma } \right)}}\)
Bước 4:
\(\widehat {ABC} = {90^o} - \widehat {HAB} = {90^o} - (\alpha - \beta )\)
Áp dụng định lí sin cho tam giác ABC ta có:
\(\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}} \Rightarrow BC = \sin \alpha .\frac{{\sin \gamma .\frac{a}{{\sin \left( {\beta - \gamma } \right)}}}}{{\sin \left( {{{90}^o} - (\alpha - \beta )} \right)}}.\).
Bài 3.10 SGK Toán 10 tập 1 – Kết nối tri thức yêu cầu chúng ta xác định các tập hợp dựa trên các điều kiện cho trước. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các khái niệm cơ bản về tập hợp, bao gồm:
Bài 3.10 thường bao gồm các câu hỏi yêu cầu xác định các tập hợp con, tập hợp giao, tập hợp hợp, hoặc tập hợp bù của một tập hợp cho trước. Ví dụ:
Cho A = {1, 2, 3, 4, 5} và B = {3, 4, 5, 6, 7}. Hãy tìm:
Để giải bài tập này, chúng ta sẽ áp dụng các định nghĩa và quy tắc về các phép toán trên tập hợp:
Để củng cố kiến thức về tập hợp và các phép toán trên tập hợp, bạn có thể thực hành thêm các bài tập tương tự. Ví dụ:
Cho C = {a, b, c, d} và D = {b, d, e, f}. Hãy tìm C ∪ D, C ∩ D, C \ D, và D \ C.
Kiến thức về tập hợp có ứng dụng rộng rãi trong nhiều lĩnh vực của toán học và khoa học máy tính, bao gồm:
Bài 3.10 trang 43 SGK Toán 10 tập 1 – Kết nối tri thức là một bài tập quan trọng giúp học sinh nắm vững kiến thức cơ bản về tập hợp và các phép toán trên tập hợp. Bằng cách hiểu rõ các khái niệm và áp dụng các quy tắc một cách chính xác, học sinh có thể giải quyết bài tập này một cách dễ dàng và hiệu quả.
Giaitoan.edu.vn hy vọng rằng lời giải chi tiết và hướng dẫn này sẽ giúp bạn hiểu rõ hơn về bài tập này và tự tin hơn trong việc học Toán 10.