Bài 3.8 trang 42 SGK Toán 10 tập 1 thuộc chương 3: Hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3.8 trang 42 SGK Toán 10 tập 1 – Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Một tàu đánh cá xuất phát từ cảng A, đi theo hướng S70E với vận tốc 70 km/h. Đi được 90 phút thì động cơ của tàu bị hỏng nên tàu trôi tự do theo hướng nam với vận tốc 8 km/h. Sau 2 giờ kể từ khi động cơ bị hỏng, tàu neo đậu được vào một hòn đảo. a) Tính khoảng cách từ cảng A tới đảo nơi tàu neo đậu. b) Xác định hướng từ cảng A tới đảo nơi tàu neo đậu.
b) Xác định hướng từ cảng A tới đảo nơi tàu neo đậu.
Lời giải chi tiết:
Theo sơ đồ, hướng từ cảng A tới đảo nơi tàu neo đậu là \(S{\alpha ^o}E\) với \({\alpha ^o} = \widehat {CAS}\).
Do BC // AS nên \(\widehat {CAS}= \widehat {ACB}\)
Áp dụng định lí sin cho tam giác ABC ta có:
\(\frac{BC}{{\sin A}} = \frac{AC}{{\sin B}} = \frac{AB}{{\sin C}}\)\( \Rightarrow \sin C = \frac{{AB.\sin B}}{AC}\)
Mà \(\widehat B = {110^o}\); \(AC \approx 111,5\); AB = 105.
\(\begin{array}{l} \Rightarrow \sin C= \frac{{105.\sin {{110}^o}}}{{111,5}} \approx 0,885\\ \Rightarrow \widehat C \approx {62^o}(do\;\widehat C < {90^o})\end{array}\)
Vậy hướng từ cảng A tới đảo nơi tàu neo đậu là \(S{62^o}E\).
Tính khoảng cách từ cảng A tới đảo nơi tàu neo đậu
Phương pháp giải:
Bước 1: Vẽ hình mô tả đường đi từ cảng A, đến nơi mà động cơ hỏng (kí hiệu là B) và hòn đảo (kí hiệu là C) nơi tàu neo đậu.
Bước 2: Tính góc \(\widehat {ABC}\), quãng đường tàu đi được sau 90 phút () và quãng đường tàu trôi tự do ().
Bước 3: Tính khoảng cách từ cảng tới nơi tàu neo đậu (đoạn AC) bằng cách áp dụng định lí cosin tại đỉnh B.
Lời giải chi tiết:
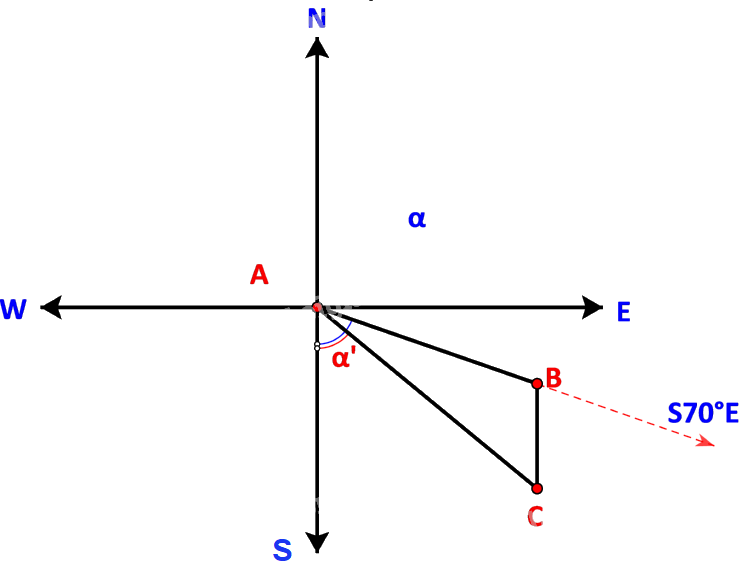
Ta có sơ đồ đường đi như sau:
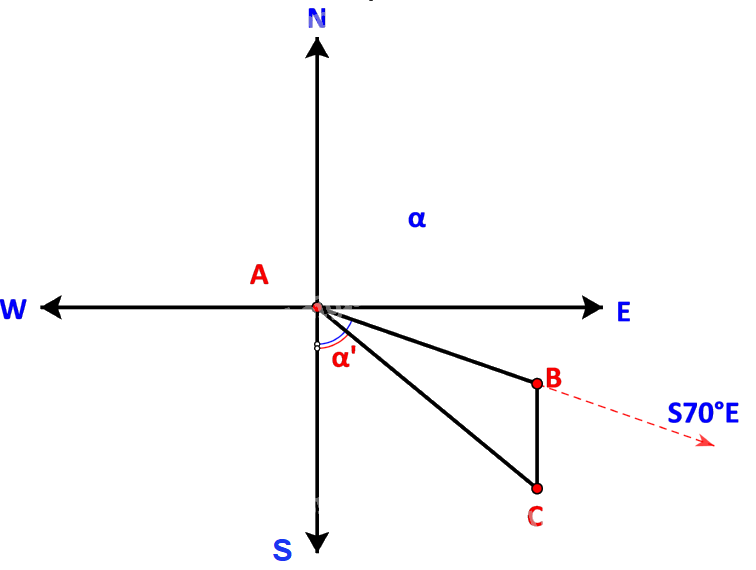
Trong đó: B là nơi động cơ bị hỏng, C là ví trí neo đậu của tàu trên hòn đảo.
Khoảng cách từ cảng A tới đảo nơi tàu neo đậu là đoạn AC.
Quãng đường tàu đi được sau 90 phút hay 1,5 giờ (ngay trước khi hỏng động cơ) là:
70.1,5 = 105 (km) hay AB = 105.
Sau 2 giờ tàu trôi tự do từ B đến C với vận tốc 8km/h , suy ra BC= 8.2 = 16 (km).
Ban đầu tàu di chuyển theo hướng \(S{70^o}E\) nên \(\widehat {BAS} = {70^o}\). Sau khi động cơ bị hỏng, tàu trôi theo hướng Nam do đó BC song song với AS.
\( \Rightarrow \widehat {ABC} = {180^o} - \widehat {BAS} = {110^o}\)
Áp dụng định lí cosin cho tam giác ABC ta có:
\({AC^2} = {BC^2} + {AB^2} - 2.AC.BC.\cos B\)
\(\begin{array}{l} \Rightarrow {AC^2} = {16^2} + {105^2} - 2.16.105.\cos {110^o} \approx 12430\\ \Rightarrow AC \approx 111,5.\end{array}\)
Vậy khoảng cách từ cảng A tới đảo nơi tàu neo đậu là khoảng 111,5 km.
Một tàu đánh cá xuất phát từ cảng A, đi theo hướng \(S{70^o}E\) với vận tốc 70 km/h. Đi được 90 phút thì động cơ của tàu bị hỏng nên tàu trôi tự do theo hướng nam với vận tốc 8 km/h. Sau 2 giờ kể từ khi động cơ bị hỏng, tàu neo đậu được vào một hòn đảo.
a) Tính khoảng cách từ cảng A tới đảo nơi tàu neo đậu.
b) Xác định hướng từ cảng A tới đảo nơi tàu neo đậu.
Tính khoảng cách từ cảng A tới đảo nơi tàu neo đậu
Phương pháp giải:
Bước 1: Vẽ hình mô tả đường đi từ cảng A, đến nơi mà động cơ hỏng (kí hiệu là B) và hòn đảo (kí hiệu là C) nơi tàu neo đậu.
Bước 2: Tính góc \(\widehat {ABC}\), quãng đường tàu đi được sau 90 phút () và quãng đường tàu trôi tự do ().
Bước 3: Tính khoảng cách từ cảng tới nơi tàu neo đậu (đoạn AC) bằng cách áp dụng định lí cosin tại đỉnh B.
Lời giải chi tiết:
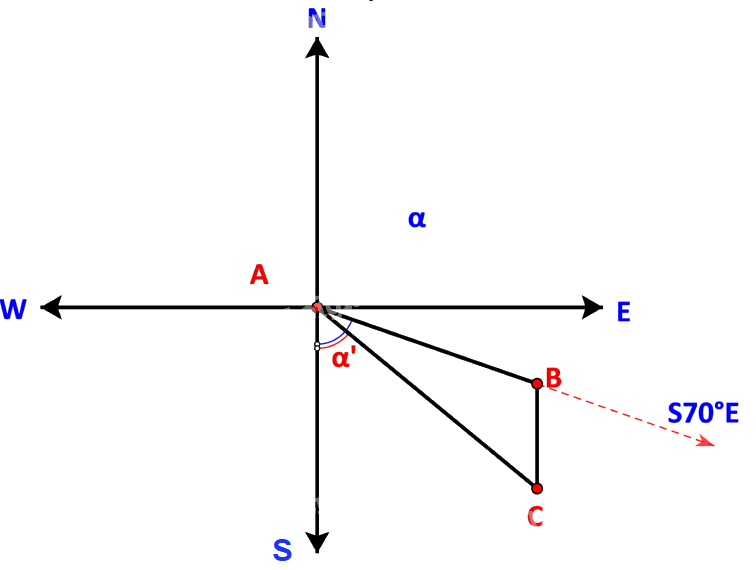
Ta có sơ đồ đường đi như sau:
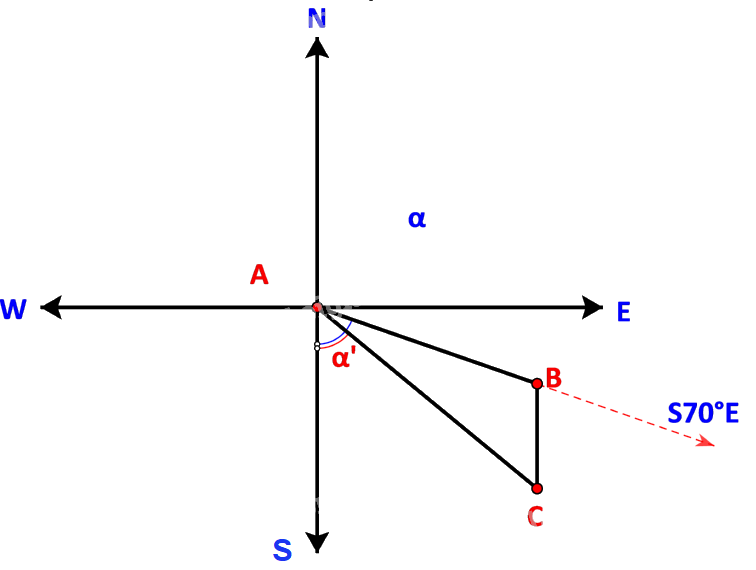
Trong đó: B là nơi động cơ bị hỏng, C là ví trí neo đậu của tàu trên hòn đảo.
Khoảng cách từ cảng A tới đảo nơi tàu neo đậu là đoạn AC.
Quãng đường tàu đi được sau 90 phút hay 1,5 giờ (ngay trước khi hỏng động cơ) là:
70.1,5 = 105 (km) hay AB = 105.
Sau 2 giờ tàu trôi tự do từ B đến C với vận tốc 8km/h , suy ra BC= 8.2 = 16 (km).
Ban đầu tàu di chuyển theo hướng \(S{70^o}E\) nên \(\widehat {BAS} = {70^o}\). Sau khi động cơ bị hỏng, tàu trôi theo hướng Nam do đó BC song song với AS.
\( \Rightarrow \widehat {ABC} = {180^o} - \widehat {BAS} = {110^o}\)
Áp dụng định lí cosin cho tam giác ABC ta có:
\({AC^2} = {BC^2} + {AB^2} - 2.AC.BC.\cos B\)
\(\begin{array}{l} \Rightarrow {AC^2} = {16^2} + {105^2} - 2.16.105.\cos {110^o} \approx 12430\\ \Rightarrow AC \approx 111,5.\end{array}\)
Vậy khoảng cách từ cảng A tới đảo nơi tàu neo đậu là khoảng 111,5 km.
b) Xác định hướng từ cảng A tới đảo nơi tàu neo đậu.
Lời giải chi tiết:
Theo sơ đồ, hướng từ cảng A tới đảo nơi tàu neo đậu là \(S{\alpha ^o}E\) với \({\alpha ^o} = \widehat {CAS}\).
Do BC // AS nên \(\widehat {CAS}= \widehat {ACB}\)
Áp dụng định lí sin cho tam giác ABC ta có:
\(\frac{BC}{{\sin A}} = \frac{AC}{{\sin B}} = \frac{AB}{{\sin C}}\)\( \Rightarrow \sin C = \frac{{AB.\sin B}}{AC}\)
Mà \(\widehat B = {110^o}\); \(AC \approx 111,5\); AB = 105.
\(\begin{array}{l} \Rightarrow \sin C= \frac{{105.\sin {{110}^o}}}{{111,5}} \approx 0,885\\ \Rightarrow \widehat C \approx {62^o}(do\;\widehat C < {90^o})\end{array}\)
Vậy hướng từ cảng A tới đảo nơi tàu neo đậu là \(S{62^o}E\).
Bài 3.8 trang 42 SGK Toán 10 tập 1 – Kết nối tri thức là một bài tập quan trọng trong chương Hàm số bậc nhất. Để giải bài tập này, học sinh cần nắm vững các khái niệm cơ bản về hàm số bậc nhất, bao gồm:
Nội dung bài tập 3.8:
(Đề bài cụ thể của bài 3.8 sẽ được trình bày tại đây. Ví dụ: Cho hàm số y = 2x - 3. Hãy tìm giá trị của y khi x = 1; x = -2; x = 0.)
Lời giải chi tiết:
Để giải bài tập này, chúng ta sẽ thực hiện các bước sau:
Ví dụ:
Kết luận:
Vậy, khi x = 1 thì y = -1; khi x = -2 thì y = -7; khi x = 0 thì y = -3.
Ngoài bài 3.8, chương Hàm số bậc nhất còn có nhiều dạng bài tập khác. Dưới đây là một số dạng bài tập thường gặp và phương pháp giải:
Lưu ý khi giải bài tập về hàm số bậc nhất:
Tài liệu tham khảo:
Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trên, các em học sinh sẽ hiểu rõ hơn về cách giải bài 3.8 trang 42 SGK Toán 10 tập 1 – Kết nối tri thức và tự tin hơn trong việc học tập môn Toán.