Chào mừng các em học sinh đến với bài giải chi tiết mục 3 trang 52, 53 sách giáo khoa Toán 10 tập 2 chương trình Kết nối tri thức. Bài viết này cung cấp lời giải đầy đủ, dễ hiểu cho từng bài tập, giúp các em nắm vững kiến thức và tự tin làm bài tập về nhà.
Giaitoan.edu.vn là địa chỉ học toán online uy tín, cung cấp giải pháp học tập toàn diện cho học sinh cấp THPT.
Tại một vùng biển giữa đất liền và một đảo, người ta phân định một đường ranh giới cách đều đất liền và đảo (H.7.28). Coi bờ biển vùng đất liền đó là một đường thẳng và đảo là hình tròn. Hỏi đường ranh giới nói trên có hình gi? Vì sao?
Xét (P) là một parabol với tiêu điểm F và đường chuẩn \(\Delta \). Gọi p là tham số tiêu của (P) và H là hình chiếu vuông góc của F trên \(\Delta \). Chọn hệ trục toạ độ Oxy Có gốc O là trung điểm của HF, tia Ox trùng tia OF (H7.27).
a) Nêu toạ độ của Fvà phương trình của \(\Delta \).
b) Giải thích vì sao điềm M(x; y) thuộc (P) khi và chỉ khi \(\sqrt {{{\left( {x - \frac{p}{2}} \right)}^2} + {y^2}} = \left| {x + \frac{p}{2}} \right|\).
Lời giải chi tiết:
a) Tọa độ điểm F là: \(F\left( {\frac{p}{2};0} \right)\) và phương trình đường chuẩn là: \(\Delta :x = - \frac{p}{2}\)
b) Ta có: \(MF = \sqrt {{{\left( {x - \frac{p}{2}} \right)}^2} + {y^2}} ,d\left( {M,\Delta } \right) = \left| {x + \frac{p}{2}} \right|\). Để M thuộc (P) thì \(MF{\rm{ }} = \;d\left( {M,\Delta } \right) \Leftrightarrow \sqrt {{{\left( {x - \frac{p}{2}} \right)}^2} + {y^2}} = \left| {x + \frac{p}{2}} \right|\)
Cho parabol (P): \(y = \frac{1}{4}{x^2}\). Xét F(0; 1) và đường thẳng\(\Delta :{\rm{ }}y{\rm{ }} + 1 = 0\) . Với điểm M(x;y) bất kì, chứng minh rằng \(MF{\rm{ }} = \;d\left( {M,\Delta } \right) \Leftrightarrow \) M(xy) thuộc (P).
Lời giải chi tiết:
Ta có: \(MF = \sqrt {{x^2} + {{\left( {y - 1} \right)}^2}} ,d\left( {M,\Delta } \right) = \left| {y + 1} \right|\).
Xét \(MF = d\left( {M,\Delta } \right) \Leftrightarrow \sqrt {{x^2} + {{\left( {y - 1} \right)}^2}} = \left| {y + 1} \right| \Leftrightarrow {x^2} + {\left( {y - 1} \right)^2} = {\left( {y + 1} \right)^2} \Leftrightarrow {x^2} = 4y \Leftrightarrow y = \frac{1}{4}{x^2}\).
Vậy tập hợp điểm M để \(MF{\rm{ }} = \;d\left( {M,\Delta } \right)\) là parabol \(y = \frac{1}{4}{x^2}\)
Tại một vùng biển giữa đất liền và một đảo, người ta phân định một đường ranh giới cách đều đất liền và đảo (H.7.28). Coi bờ biển vùng đất liền đó là một đường thẳng và đảo là hình tròn. Hỏi đường ranh giới nói trên có hình gi? Vì sao?
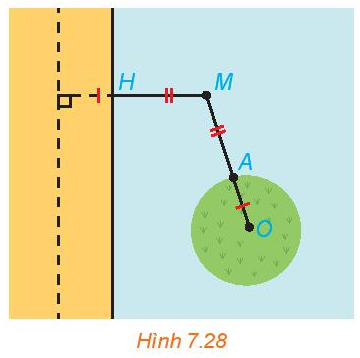
Phương pháp giải:
Lấy d là đường thẳng song song với bờ biển cách bờ biển một khoảng bằng bán kính OA.
Lời giải chi tiết:
Gọi d là đường thẳng nằm trong đất liền, song song với bờ biển và cách bờ biển một khoảng bằng bán kính OA.
Ta có: \(d\left( {M,d} \right) = MH + R = MA + AO = MO\)
Vậy tập hợp điểm M thuộc (P) có tiêu điểm là O. Đường chuẩn là d. Do đó đường ranh giới cần tìm là đường parabol (P).
Cho parabol (P): \(y = \frac{1}{4}{x^2}\). Xét F(0; 1) và đường thẳng\(\Delta :{\rm{ }}y{\rm{ }} + 1 = 0\) . Với điểm M(x;y) bất kì, chứng minh rằng \(MF{\rm{ }} = \;d\left( {M,\Delta } \right) \Leftrightarrow \) M(xy) thuộc (P).
Lời giải chi tiết:
Ta có: \(MF = \sqrt {{x^2} + {{\left( {y - 1} \right)}^2}} ,d\left( {M,\Delta } \right) = \left| {y + 1} \right|\).
Xét \(MF = d\left( {M,\Delta } \right) \Leftrightarrow \sqrt {{x^2} + {{\left( {y - 1} \right)}^2}} = \left| {y + 1} \right| \Leftrightarrow {x^2} + {\left( {y - 1} \right)^2} = {\left( {y + 1} \right)^2} \Leftrightarrow {x^2} = 4y \Leftrightarrow y = \frac{1}{4}{x^2}\).
Vậy tập hợp điểm M để \(MF{\rm{ }} = \;d\left( {M,\Delta } \right)\) là parabol \(y = \frac{1}{4}{x^2}\)
Xét (P) là một parabol với tiêu điểm F và đường chuẩn \(\Delta \). Gọi p là tham số tiêu của (P) và H là hình chiếu vuông góc của F trên \(\Delta \). Chọn hệ trục toạ độ Oxy Có gốc O là trung điểm của HF, tia Ox trùng tia OF (H7.27).
a) Nêu toạ độ của Fvà phương trình của \(\Delta \).
b) Giải thích vì sao điềm M(x; y) thuộc (P) khi và chỉ khi \(\sqrt {{{\left( {x - \frac{p}{2}} \right)}^2} + {y^2}} = \left| {x + \frac{p}{2}} \right|\).
Lời giải chi tiết:
a) Tọa độ điểm F là: \(F\left( {\frac{p}{2};0} \right)\) và phương trình đường chuẩn là: \(\Delta :x = - \frac{p}{2}\)
b) Ta có: \(MF = \sqrt {{{\left( {x - \frac{p}{2}} \right)}^2} + {y^2}} ,d\left( {M,\Delta } \right) = \left| {x + \frac{p}{2}} \right|\). Để M thuộc (P) thì \(MF{\rm{ }} = \;d\left( {M,\Delta } \right) \Leftrightarrow \sqrt {{{\left( {x - \frac{p}{2}} \right)}^2} + {y^2}} = \left| {x + \frac{p}{2}} \right|\)
Tại một vùng biển giữa đất liền và một đảo, người ta phân định một đường ranh giới cách đều đất liền và đảo (H.7.28). Coi bờ biển vùng đất liền đó là một đường thẳng và đảo là hình tròn. Hỏi đường ranh giới nói trên có hình gi? Vì sao?
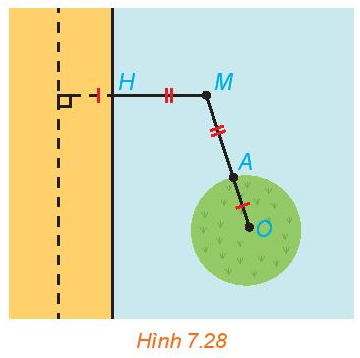
Phương pháp giải:
Lấy d là đường thẳng song song với bờ biển cách bờ biển một khoảng bằng bán kính OA.
Lời giải chi tiết:
Gọi d là đường thẳng nằm trong đất liền, song song với bờ biển và cách bờ biển một khoảng bằng bán kính OA.
Ta có: \(d\left( {M,d} \right) = MH + R = MA + AO = MO\)
Vậy tập hợp điểm M thuộc (P) có tiêu điểm là O. Đường chuẩn là d. Do đó đường ranh giới cần tìm là đường parabol (P).
Mục 3 trong SGK Toán 10 tập 2 Kết nối tri thức tập trung vào việc ôn tập chương 3, bao gồm các kiến thức về vectơ, các phép toán vectơ, và ứng dụng của vectơ trong hình học. Việc nắm vững kiến thức này là nền tảng quan trọng cho các chương học tiếp theo. Bài viết này sẽ đi sâu vào giải chi tiết từng bài tập trong mục 3 trang 52, 53, giúp các em hiểu rõ phương pháp giải và áp dụng vào các bài tập tương tự.
Mục 3 trang 52, 53 bao gồm các bài tập tổng hợp, đòi hỏi học sinh phải vận dụng linh hoạt các kiến thức đã học về vectơ. Các bài tập thường liên quan đến:
Bài 1 yêu cầu học sinh tìm tọa độ của vectơ dựa trên tọa độ của các điểm. Để giải bài này, các em cần nắm vững công thức tính tọa độ của vectơ khi biết tọa độ của các điểm đầu và điểm cuối. Ví dụ, nếu A(xA, yA) và B(xB, yB) thì vectơ AB có tọa độ (xB - xA, yB - yA).
Bài 2 tập trung vào việc thực hiện các phép toán cộng, trừ, nhân vectơ với một số. Các em cần nhớ các quy tắc sau:
Bài 3 yêu cầu học sinh chứng minh các đẳng thức vectơ. Để giải bài này, các em cần sử dụng các quy tắc biến đổi vectơ, chẳng hạn như quy tắc hình bình hành, quy tắc tam giác, và các tính chất của phép cộng, trừ vectơ.
Bài 4 là bài tập vận dụng, yêu cầu học sinh sử dụng vectơ để giải các bài toán hình học phẳng. Ví dụ, chứng minh hai đường thẳng song song, chứng minh ba điểm thẳng hàng, hoặc tính diện tích của một hình.
Để giải tốt các bài tập về vectơ, các em cần:
Ngoài SGK Toán 10 tập 2 Kết nối tri thức, các em có thể tham khảo thêm các tài liệu sau:
Hy vọng bài giải chi tiết mục 3 trang 52, 53 SGK Toán 10 tập 2 Kết nối tri thức này sẽ giúp các em học tốt môn Toán. Chúc các em học tập hiệu quả!