Bài 9.9 trang 86 SGK Toán 10 – Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 10. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 9.9 trang 86 SGK Toán 10 – Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Gieo liên tiếp một con xúc xắc và một đồng xu.
Đề bài
Gieo liên tiếp một con xúc xắc và một đồng xu.
a) Vẽ sơ đồ hình cây mô tả các phần tử của không gian mẫu.
b) Tính xác suất của các biến cố sau: F: “Đồng xu xuất hiện mặt ngửa"; G: “Đồng xu xuất hiện mặt sấp hoặc Số chấm xuất hiện trên con xúc xắc là 5".
Lời giải chi tiết
a) Sơ đồ cây
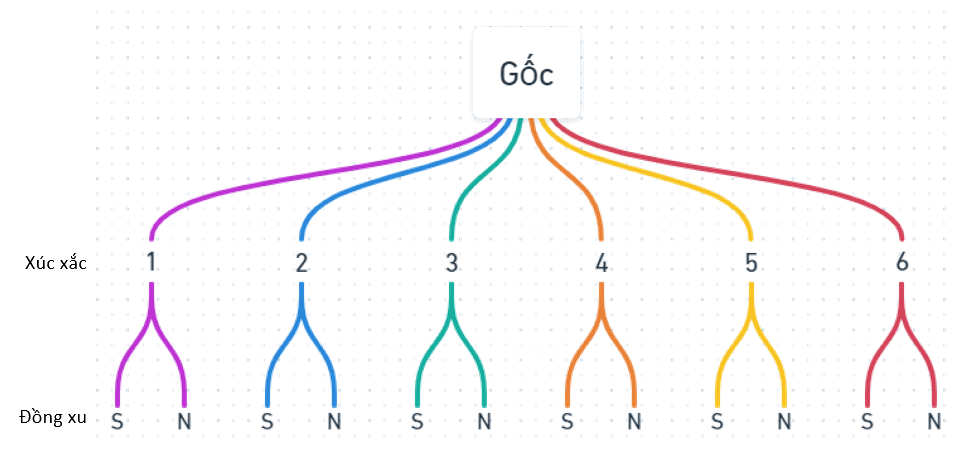
b) Từ sơ đồ cây ta có \(n\left( \Omega \right) = 12\).
Ta có \(F = \left\{ {\left( {1,N} \right);\left( {2,N} \right);\left( {3,N} \right);\left( {4,N} \right);\left( {5,N} \right);\left( {6,N} \right)} \right\}\). Suy ra \(n\left( F \right) = 6\). Vậy \(P\left( F \right) = \frac{6}{{12}} = 0,5\).
\(G = \left\{ {\left( {1,S} \right);\left( {2,S} \right);\left( {3,S} \right);\left( {4,S} \right);\left( {5,S} \right);\left( {6,S} \right);\left( {5,N} \right)} \right\}\). Suy ra \(n\left( G \right) = 7\). Vậy \(P\left( G \right) = \frac{7}{{12}}\).
Bài 9.9 trang 86 SGK Toán 10 – Kết nối tri thức là một bài toán ứng dụng thực tế về vectơ trong hình học. Để giải bài toán này, học sinh cần nắm vững các kiến thức cơ bản về vectơ, bao gồm:
Đề bài: Cho tam giác ABC. Gọi M là trung điểm của BC. G là trọng tâm của tam giác ABC. Chứng minh rằng: GA = 2GM
Để chứng minh GA = 2GM, ta sẽ sử dụng các tính chất của trọng tâm và trung điểm của tam giác.
GA = AG = 2/3 AM và 2GM = 2 * (1/3 AM) = 2/3 AM
Vậy, GA = 2GM (điều phải chứng minh).
Bài toán này là một ví dụ điển hình về ứng dụng của vectơ trong hình học. Việc sử dụng vectơ giúp chúng ta biểu diễn các đại lượng hình học một cách ngắn gọn và dễ dàng, đồng thời giúp chúng ta chứng minh các tính chất hình học một cách chặt chẽ.
Ngoài ra, bài toán này cũng có thể được giải bằng phương pháp hình học thuần túy, tuy nhiên, phương pháp vectơ thường cho kết quả nhanh chóng và hiệu quả hơn.
Để củng cố kiến thức về vectơ và ứng dụng của nó trong hình học, các em học sinh có thể tự giải các bài tập tương tự sau:
Hy vọng rằng lời giải chi tiết và dễ hiểu bài 9.9 trang 86 SGK Toán 10 – Kết nối tri thức trên đây sẽ giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự. Chúc các em học tập tốt!
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.