Bài 9.10 trang 87 SGK Toán 10 – Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 10. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học để giải quyết vấn đề.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 9.10 trang 87 SGK Toán 10 – Kết nối tri thức, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Trên một phố có hai quán ăn X, Y. Ba bạn Sơn, Hải, Văn mỗi người chọn ngẫu nhiên một quán ăn. a) Vẽ sơ đồ hình cây mô tả các phần tử của không gian mẫu. b) Tính xác suất của biến cố “Hai bạn vào quán X, bạn còn lại vào quán Y.
Đề bài
Trên một phố có hai quán ăn X, Y. Ba bạn Sơn, Hải, Văn mỗi người chọn ngẫu nhiên một quán ăn.
a) Vẽ sơ đồ hình cây mô tả các phần tử của không gian mẫu.
b) Tính xác suất của biến cố “Hai bạn vào quán X, bạn còn lại vào quán Y.
Lời giải chi tiết
a) Sơ đồ cây
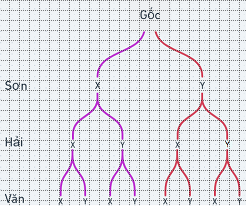
b) Dựa vào sơ đồ cây ta có \(n\left( \Omega \right) = 8\).
Gọi F là biến cố: “Hai bạn vào quán X, bạn còn lại vào quán Y”.
Ta có \(F = \left\{ {XXY;XYX;YXX} \right\}\). Suy ra \(n\left( F \right) = 3\). Vậy \(P\left( F \right) = \frac{3}{8}\).
Bài 9.10 trang 87 SGK Toán 10 – Kết nối tri thức thuộc chương 3: Vectơ trong mặt phẳng. Bài toán này thường yêu cầu học sinh sử dụng các kiến thức về:
Trước khi đi vào giải bài tập, chúng ta cần đọc kỹ đề bài, xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Phân tích bài toán giúp chúng ta lựa chọn phương pháp giải phù hợp và tránh sai sót.
Để giải bài 9.10 trang 87 SGK Toán 10 – Kết nối tri thức, chúng ta thực hiện theo các bước sau:
Giả sử đề bài yêu cầu tính độ dài của vectơ AB, với A(x1, y1) và B(x2, y2). Ta có công thức tính độ dài của vectơ AB như sau:
|AB| = √((x2 - x1)² + (y2 - y1)²)
Khi giải bài tập về vectơ, cần chú ý các điểm sau:
Để củng cố kiến thức về vectơ, các em có thể làm thêm các bài tập tương tự sau:
Bài 9.10 trang 87 SGK Toán 10 – Kết nối tri thức là một bài tập quan trọng giúp các em học sinh hiểu rõ hơn về vectơ và ứng dụng của vectơ trong hình học. Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trên đây, các em sẽ tự tin giải quyết bài tập này và đạt kết quả tốt trong môn Toán.
| Công thức | Mô tả |
|---|---|
| a + b = b + a | Tính giao hoán của phép cộng vectơ |
| (a + b) + c = a + (b + c) | Tính kết hợp của phép cộng vectơ |
| a.b = |a||b|cos(θ) | Công thức tính tích vô hướng của hai vectơ |