Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 tập 1 Kết nối tri thức tại giaitoan.edu.vn. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập trong SGK, giúp các em nắm vững kiến thức và tự tin hơn trong học tập.
Mục 1 trang 34, 35 tập trung vào các khái niệm cơ bản về tập hợp và các phép toán trên tập hợp. Việc hiểu rõ những kiến thức này là nền tảng quan trọng cho các bài học tiếp theo.
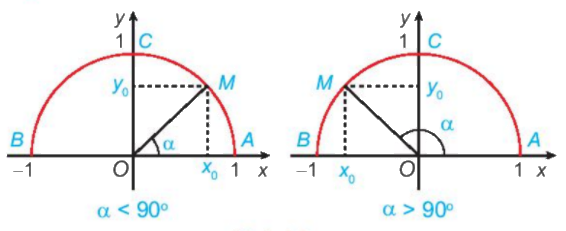
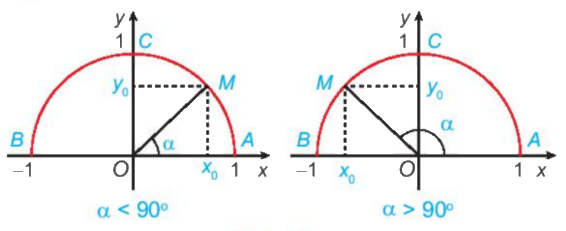
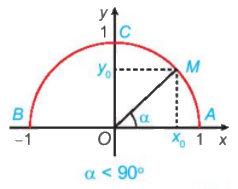
a) Nêu nhận xét về vị trí điểm M trên nửa đường tròn đơn vị trong mỗi trường hợp sau: Tìm các giá trị lượng giác của góc 120
a) Nêu nhận xét về vị trí điểm M trên nửa đường tròn đơn vị trong mỗi trường hợp sau:
\(\begin{array}{l}\alpha = {90^o};\\\alpha < {90^o};\\\alpha > {90^o}.\end{array}\)
b) Khi \({0^o} < \alpha < {90^o}\), nêu mối quan hệ giữa \(\cos \alpha ,\;\sin \alpha \) với hoành độ và tung độ của điểm M.
Phương pháp giải:
a) Quan sát góc\(\alpha = \widehat {xOM}\) trong các trường hợp tương ứng. Khi ấy M thuộc cung nào?
b) Khi \({0^o} < \alpha < {90^o}\) thì \(\cos \alpha = \frac{{\left| {{x_0}} \right|}}{{OM}},\;\sin \alpha = \frac{{\left| {{y_0}} \right|}}{{OM}};\) trong đó \(OM = R = 1\).
Lời giải chi tiết:
a) Khi \(\alpha = {90^o}\), điểm M trùng với điểm C. (Vì \(\widehat {xOC} = \widehat {AOC} = {90^o}\))
Khi \(\alpha < {90^o}\), điểm M thuộc vào cung AC (bên phải trục tung)
Khi \(\alpha > {90^o}\), điểm M thuộc vào cung BC (bên trái trục tung)
b) Khi \({0^o} < \alpha < {90^o}\) , ta có:
\(\begin{array}{l}\cos \alpha = \frac{{\left| {{x_0}} \right|}}{{OM}} = \left| {{x_0}} \right| = {x_0};\\\sin \alpha = \frac{{\left| {{y_0}} \right|}}{{OM}} = \left| {{y_o}} \right| = {y_o}\end{array}\)
Vì \(OM = R = 1\); \({x_0} \in \)tia \(Ox\)nên \({x_0} > 0\); \({y_0} \in \)tia \(Oy\)nên \({y_0} > 0\)
Vậy \(\cos \alpha \) là hoành độ \({x_0}\)của điểm M, \(\sin \alpha \) là tung độ \({y_0}\) của điểm M.
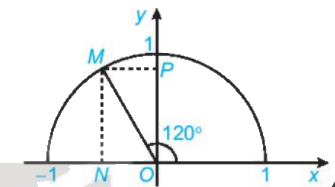
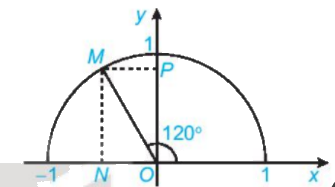
Tìm các giá trị lượng giác của góc \({120^o}\) (H.3.4)
Phương pháp giải:
Gọi M là điểm trên nửa đường tròn đơn vị sao cho \(\widehat {xOM} = {120^o}\)
Khi đó hoành độ và tung độ của điểm M lần lượt là các giá trị \(\cos {120^o},\;\sin {120^o}\)
Từ đó suy ra \(\;\tan {120^o} = \dfrac{{\sin {{120}^o}}}{{\cos {{120}^o}}},\;\;\cot {120^o} = \dfrac{{\cos {{120}^o}}}{{\sin {{120}^o}}}.\)
Lời giải chi tiết:
Gọi M là điểm trên nửa đường tròn đơn vị sao cho \(\widehat {xOM} = {120^o}\)
Gọi N, P tương ứng là hình chiếu vuông góc của M lên các trục Ox, Oy.
Vì \(\widehat {xOM} = {120^o} > {90^o}\) nên M nằm bên trái trục tung.
Khi đó:\(\;\cos {120^o} = - \,\;\overline {ON} ,\;\;\sin {120^o} = \overline {OP} \)
Vì \(\widehat {xOM} = {120^o}\) nên \(\widehat {NOM} = {180^o} - {120^o} = {60^o}\) và \(\widehat {POM} = {120^o} - {90^o} = {30^o}\)
Vậy các tam giác \(\Delta MON\) và \(\Delta MOP\) vuông tại N, p và có một góc bằng \({30^o}\)
\( \Rightarrow ON = MP = \frac{1}{2}OM = \frac{1}{2}\)(Trong tam giác vuông, cạnh đối diện góc \({30^o}\) bằng một nửa cạnh huyền)
Và \(OP = MN = \sqrt {O{M^2} - O{N^2}} = \sqrt {{1^2} - {{\left( {\frac{1}{2}} \right)}^2}} = \frac{{\sqrt 3 }}{2}\)
Vậy điểm M có tọa độ là \(\left( { - \frac{1}{2};\frac{{\sqrt 3 }}{2}} \right)\).
Và \(\cos {120^o} = - \frac{1}{2};\;\;\;\sin {120^o} = \frac{{\sqrt 3 }}{2}\)
\(\begin{array}{l}\; \Rightarrow \;\tan {120^o} = \frac{{\sin {{120}^o}}}{{\cos {{120}^o}}} = \frac{{\sqrt 3 }}{2}:\left( { - \frac{1}{2}} \right) = - \sqrt 3 ;\\\cot {120^o} = \frac{{\cos {{120}^o}}}{{\sin {{120}^o}}} = \left( { - \frac{1}{2}} \right):\frac{{\sqrt 3 }}{2} = \frac{{ - 1}}{{\sqrt 3 }} = - \frac{{\sqrt 3 }}{3}.\end{array}\)
Chú ý
Ta có thể sử dụng máy tính cầm tay để tính các giá trị lượng giác góc \({120^o}\)
Với các loại máy tính fx-570 ES (VN hoặc VN PLUS) ta làm như sau:
Bấm phím “SHIFT” “MODE” rồi bấm phím “3” (để chọn đơn vị độ)
Tính \(\sin {120^o}\), bấm phím: sin 1 2 0 \(^o\)’’’ = ta được kết quả là \(\frac{{\sqrt 3 }}{2}\)
Tính \(\cos {120^o}\),bấm phím: cos 1 2 0 \(^o\)’’’ = ta được kết quả là \(\frac{{ - 1}}{2}\)
Tính \(\tan {120^o}\), bấm phím: tan 1 2 0 \(^o\)’’’ = ta được kết quả là \( - \sqrt 3 \)
( Để tính \(\cot {120^o}\), ta tính \(1:\tan {120^o}\))
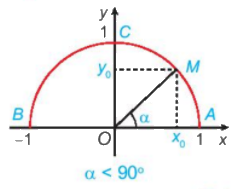
a) Nêu nhận xét về vị trí điểm M trên nửa đường tròn đơn vị trong mỗi trường hợp sau:
\(\begin{array}{l}\alpha = {90^o};\\\alpha < {90^o};\\\alpha > {90^o}.\end{array}\)
b) Khi \({0^o} < \alpha < {90^o}\), nêu mối quan hệ giữa \(\cos \alpha ,\;\sin \alpha \) với hoành độ và tung độ của điểm M.
Phương pháp giải:
a) Quan sát góc\(\alpha = \widehat {xOM}\) trong các trường hợp tương ứng. Khi ấy M thuộc cung nào?
b) Khi \({0^o} < \alpha < {90^o}\) thì \(\cos \alpha = \frac{{\left| {{x_0}} \right|}}{{OM}},\;\sin \alpha = \frac{{\left| {{y_0}} \right|}}{{OM}};\) trong đó \(OM = R = 1\).
Lời giải chi tiết:
a) Khi \(\alpha = {90^o}\), điểm M trùng với điểm C. (Vì \(\widehat {xOC} = \widehat {AOC} = {90^o}\))
Khi \(\alpha < {90^o}\), điểm M thuộc vào cung AC (bên phải trục tung)
Khi \(\alpha > {90^o}\), điểm M thuộc vào cung BC (bên trái trục tung)
b) Khi \({0^o} < \alpha < {90^o}\) , ta có:
\(\begin{array}{l}\cos \alpha = \frac{{\left| {{x_0}} \right|}}{{OM}} = \left| {{x_0}} \right| = {x_0};\\\sin \alpha = \frac{{\left| {{y_0}} \right|}}{{OM}} = \left| {{y_o}} \right| = {y_o}\end{array}\)
Vì \(OM = R = 1\); \({x_0} \in \)tia \(Ox\)nên \({x_0} > 0\); \({y_0} \in \)tia \(Oy\)nên \({y_0} > 0\)
Vậy \(\cos \alpha \) là hoành độ \({x_0}\)của điểm M, \(\sin \alpha \) là tung độ \({y_0}\) của điểm M.
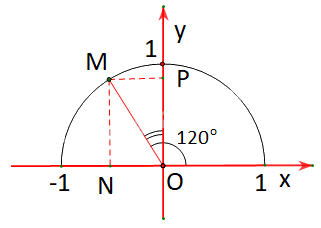
Tìm các giá trị lượng giác của góc \({120^o}\) (H.3.4)
Phương pháp giải:
Gọi M là điểm trên nửa đường tròn đơn vị sao cho \(\widehat {xOM} = {120^o}\)
Khi đó hoành độ và tung độ của điểm M lần lượt là các giá trị \(\cos {120^o},\;\sin {120^o}\)
Từ đó suy ra \(\;\tan {120^o} = \dfrac{{\sin {{120}^o}}}{{\cos {{120}^o}}},\;\;\cot {120^o} = \dfrac{{\cos {{120}^o}}}{{\sin {{120}^o}}}.\)
Lời giải chi tiết:
Gọi M là điểm trên nửa đường tròn đơn vị sao cho \(\widehat {xOM} = {120^o}\)
Gọi N, P tương ứng là hình chiếu vuông góc của M lên các trục Ox, Oy.
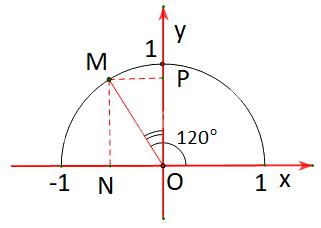
Vì \(\widehat {xOM} = {120^o} > {90^o}\) nên M nằm bên trái trục tung.
Khi đó:\(\;\cos {120^o} = - \,\;\overline {ON} ,\;\;\sin {120^o} = \overline {OP} \)
Vì \(\widehat {xOM} = {120^o}\) nên \(\widehat {NOM} = {180^o} - {120^o} = {60^o}\) và \(\widehat {POM} = {120^o} - {90^o} = {30^o}\)
Vậy các tam giác \(\Delta MON\) và \(\Delta MOP\) vuông tại N, p và có một góc bằng \({30^o}\)
\( \Rightarrow ON = MP = \frac{1}{2}OM = \frac{1}{2}\)(Trong tam giác vuông, cạnh đối diện góc \({30^o}\) bằng một nửa cạnh huyền)
Và \(OP = MN = \sqrt {O{M^2} - O{N^2}} = \sqrt {{1^2} - {{\left( {\frac{1}{2}} \right)}^2}} = \frac{{\sqrt 3 }}{2}\)
Vậy điểm M có tọa độ là \(\left( { - \frac{1}{2};\frac{{\sqrt 3 }}{2}} \right)\).
Và \(\cos {120^o} = - \frac{1}{2};\;\;\;\sin {120^o} = \frac{{\sqrt 3 }}{2}\)
\(\begin{array}{l}\; \Rightarrow \;\tan {120^o} = \frac{{\sin {{120}^o}}}{{\cos {{120}^o}}} = \frac{{\sqrt 3 }}{2}:\left( { - \frac{1}{2}} \right) = - \sqrt 3 ;\\\cot {120^o} = \frac{{\cos {{120}^o}}}{{\sin {{120}^o}}} = \left( { - \frac{1}{2}} \right):\frac{{\sqrt 3 }}{2} = \frac{{ - 1}}{{\sqrt 3 }} = - \frac{{\sqrt 3 }}{3}.\end{array}\)
Chú ý
Ta có thể sử dụng máy tính cầm tay để tính các giá trị lượng giác góc \({120^o}\)
Với các loại máy tính fx-570 ES (VN hoặc VN PLUS) ta làm như sau:
Bấm phím “SHIFT” “MODE” rồi bấm phím “3” (để chọn đơn vị độ)
Tính \(\sin {120^o}\), bấm phím: sin 1 2 0 \(^o\)’’’ = ta được kết quả là \(\frac{{\sqrt 3 }}{2}\)
Tính \(\cos {120^o}\),bấm phím: cos 1 2 0 \(^o\)’’’ = ta được kết quả là \(\frac{{ - 1}}{2}\)
Tính \(\tan {120^o}\), bấm phím: tan 1 2 0 \(^o\)’’’ = ta được kết quả là \( - \sqrt 3 \)
( Để tính \(\cot {120^o}\), ta tính \(1:\tan {120^o}\))
Mục 1 của chương trình Toán 10 tập 1 Kết nối tri thức giới thiệu về tập hợp, một khái niệm nền tảng trong toán học. Các em sẽ được làm quen với các khái niệm như phần tử của tập hợp, cách biểu diễn tập hợp, các phép toán trên tập hợp (hợp, giao, hiệu, bù) và các tính chất của chúng. Việc nắm vững những kiến thức này là vô cùng quan trọng để giải quyết các bài toán liên quan đến tập hợp và chuẩn bị cho các chương học tiếp theo.
Để giải tốt các bài tập trong Mục 1, các em cần nắm vững các khái niệm và tính chất của tập hợp. Dưới đây là một số phương pháp giải bài tập thường gặp:
Dưới đây là giải chi tiết một số bài tập tiêu biểu trong Mục 1 trang 34, 35 SGK Toán 10 tập 1 Kết nối tri thức:
Đề bài: Liệt kê các phần tử của các tập hợp sau: A = {x | x là số tự nhiên nhỏ hơn 10}; B = {x | x là số chẵn nhỏ hơn 10}; C = {x | x là số nguyên tố nhỏ hơn 10}.
Giải:
Đề bài: Cho hai tập hợp A = {1, 2, 3, 4} và B = {3, 4, 5, 6}. Tìm A ∪ B, A ∩ B, A \ B, B \ A.
Giải:
Để củng cố kiến thức về tập hợp và các phép toán trên tập hợp, các em có thể làm thêm các bài tập trong SGK và các tài liệu tham khảo khác. Ngoài ra, các em cũng có thể tham gia các diễn đàn, nhóm học tập trực tuyến để trao đổi kiến thức và kinh nghiệm với các bạn cùng lớp.
Mục 1 trang 34, 35 SGK Toán 10 tập 1 Kết nối tri thức là một phần quan trọng trong chương trình học. Việc nắm vững kiến thức và kỹ năng giải bài tập trong mục này sẽ giúp các em học tốt môn Toán và đạt kết quả cao trong các kỳ thi.