Bài 3.14 trang 44 SGK Toán 10 tập 1 thuộc chương 3: Hàm số bậc hai. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai, parabol, và các yếu tố của parabol để giải quyết các bài toán cụ thể.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu, giúp bạn hiểu rõ phương pháp giải và tự tin làm bài tập.
Tính giá trị của các biểu thức sau:
Đề bài
Tính giá trị của các biểu thức sau:
a) \(M = \sin {45^o}.\cos {45^o} + \sin {30^o}\)
b) \(N = \sin {60^o}.\cos {30^o} + \frac{1}{2}.\sin {45^o}.\cos {45^o}\)
c) \(P = 1 + {\tan ^2}{60^o}\)
d) \(Q = \frac{1}{{{{\sin }^2}{{120}^o}}} - {\cot ^2}{120^o}.\)
Phương pháp giải - Xem chi tiết
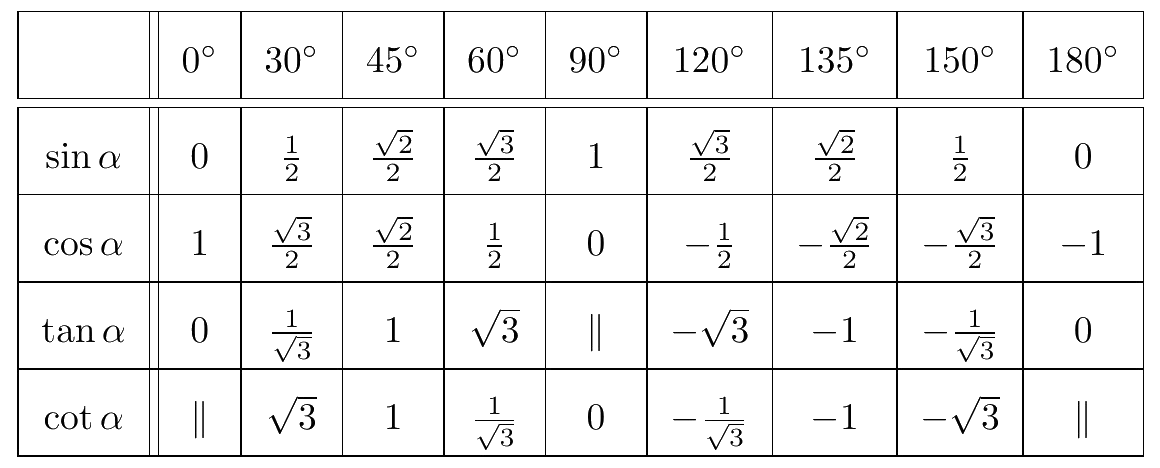
Bảng giá trị lượng giác của các góc đặc biệt
Lời giải chi tiết
a) \(M = \sin {45^o}.\cos {45^o} + \sin {30^o}\)
Ta có: \(\left\{ \begin{array}{l}\sin {45^o} = \cos {45^o} = \frac{{\sqrt 2 }}{2};\;\\\sin {30^o} = \frac{1}{2}\end{array} \right.\)
Thay vào M, ta được: \(M = \frac{{\sqrt 2 }}{2}.\frac{{\sqrt 2 }}{2} + \frac{1}{2} = \frac{2}{4} + \frac{1}{2} = 1\)
b) \(N = \sin {60^o}.\cos {30^o} + \frac{1}{2}.\sin {45^o}.\cos {45^o}\)
Ta có: \(\sin {60^o} = \frac{{\sqrt 3 }}{2};\;\;\cos {30^o} = \frac{{\sqrt 3 }}{2};\;\sin {45^o} = \frac{{\sqrt 2 }}{2};\, \cos {45^o}= \frac{{\sqrt 2 }}{2}\)
Thay vào N, ta được: \(N = \frac{{\sqrt 3 }}{2}.\frac{{\sqrt 3 }}{2} + \frac{1}{2}.\frac{{\sqrt 2 }}{2}.\frac{{\sqrt 2 }}{2} = \frac{3}{4} + \frac{1}{4} = 1\)
c) \(P = 1 + {\tan ^2}{60^o}\)
Ta có: \(\tan {60^o} = \sqrt 3 \)
Thay vào P, ta được: \(Q = 1 + {\left( {\sqrt 3 } \right)^2} = 4.\)
d) \(Q = \frac{1}{{{{\sin }^2}{{120}^o}}} - {\cot ^2}{120^o}.\)
Ta có: \(\sin {120^o} = \frac{{\sqrt 3 }}{2};\;\;\cot {120^o} = \frac{{ - 1}}{{\sqrt 3 }}\)
Thay vào P, ta được: \(Q = \frac{1}{{{{\left( {\frac{{\sqrt 3 }}{2}} \right)}^2}}} - \;{\left( {\frac{{ - 1}}{{\sqrt 3 }}} \right)^2} = \frac{1}{{\frac{3}{4}}} - \;\frac{1}{3} = \;\frac{4}{3} - \;\frac{1}{3} = 1.\)
Bài 3.14 SGK Toán 10 tập 1 – Kết nối tri thức yêu cầu học sinh xác định các yếu tố của parabol và vẽ đồ thị hàm số bậc hai. Để giải bài tập này, chúng ta cần nắm vững các kiến thức sau:
Để giải bài 3.14, chúng ta sẽ thực hiện các bước sau:
Ví dụ, xét hàm số y = x2 - 4x + 3:
Dựa vào các thông tin trên, ta có thể vẽ được đồ thị hàm số y = x2 - 4x + 3.
Để củng cố kiến thức về hàm số bậc hai và parabol, bạn có thể luyện tập thêm các bài tập tương tự. Các bài tập này thường yêu cầu:
Khi giải các bài tập này, bạn cần chú ý:
Để học tốt môn Toán 10, bạn có thể tham khảo thêm các tài liệu sau:
Bài 3.14 trang 44 SGK Toán 10 tập 1 – Kết nối tri thức là một bài tập quan trọng giúp học sinh hiểu rõ hơn về hàm số bậc hai và parabol. Hy vọng với hướng dẫn chi tiết và các bài tập tương tự, bạn sẽ tự tin giải quyết bài tập này và đạt kết quả tốt trong môn Toán 10.