Giaitoan.edu.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 2 trang 39, 40 sách giáo khoa Toán 10 tập 1 chương trình Kết nối tri thức. Bài viết này sẽ giúp các em học sinh nắm vững kiến thức, hiểu rõ phương pháp giải và tự tin làm bài tập.
Chúng tôi cung cấp đáp án đầy đủ, kèm theo các bước giải chi tiết, rõ ràng, giúp các em dễ dàng theo dõi và áp dụng vào các bài tập tương tự.
Trong mỗi hình dưới dây, hãy tính R theo a và sinA. Cho tam giác ABC có b = 8, c = 5 và B=80. Tính số đo các góc, bán kính đường tròn ngoại tiếp và độ dài cạnh còn lại của tam giác.
Cho tam giác ABC có b = 8, c = 5 và \(\widehat B = {80^o}\). Tính số đo các góc, bán kính đường tròn ngoại tiếp và độ dài cạnh còn lại của tam giác.
Phương pháp giải:
Bước 1: Tính sin\(\widehat C\), bằng cách áp dụng định lí sin tại đỉnh B và C. Từ đó suy ra số đo góc C.
Bước 2: Tính \(\widehat A\) và suy ra a dựa vào định lí sin.
Bước 3: Tính R.
Lời giải chi tiết:
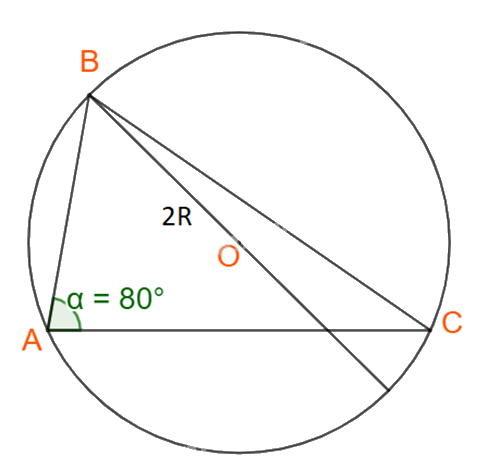
Áp dụng định lí sin cho tam giác ABC ta có:
\(\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}} = 2R\)
\(\begin{array}{l} \Rightarrow \sin C = \frac{{c.\sin B}}{b} = \frac{{5.\sin {{80}^o}}}{8} \approx 0,6155\\ \Leftrightarrow \widehat C \approx {38^o}\end{array}\)
Lại có: \(\widehat A = {180^o} - \widehat B - \widehat C = {180^o} - {80^o} - {38^o} = {62^o}\)
Theo định lí sin, ta suy ra \(a = \sin A.\dfrac{b}{{\sin B}} = \sin {62^o}\dfrac{8}{{\sin {{80}^o}}} \approx 7,17\)
Và \(2R = \dfrac{b}{{\sin B}} \Rightarrow R = \dfrac{b}{{2\sin B}} = \dfrac{8}{{2\sin {{80}^o}}} \approx 4,062.\)
Vậy tam giác ABC có \(\widehat A = {62^o}\); \(\widehat C \approx {38^o}\); \(a \approx 7,17\) và \(R \approx 4,062.\)
Trong mỗi hình dưới dây, hãy tính R theo a và sinA.
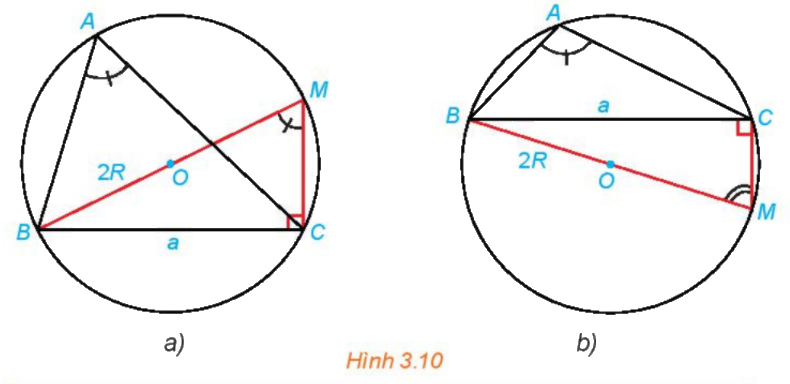
Phương pháp giải:
Bước 1: Tính sin M. Từ đó tính R theo a và sinM.
Bước 2: Tìm mối liên hệ giữa sinA và sinM, suy ra công thức tính R theo sinA.
Lời giải chi tiết:
Xét tam giác MBC vuông tại C ta có:
\(\sin M = \dfrac{{BC}}{{BM}} = \dfrac{a}{{2R}} \Rightarrow R = \dfrac{a}{{2\sin M}}\)
Lại có: Hình 3.10 a: \(\widehat A = \widehat M\) (cùng chắn cung nhỏ BC )
\( \Rightarrow \sin A = \sin M \Rightarrow R = \dfrac{a}{{2\sin A}}\)
Hình 3.10b: \(\widehat A + \widehat M = {180^o}\) (cùng tứ giác ABMC nội tiếp đường tròn (O,R))
\( \Rightarrow \sin A = \sin M \Rightarrow R = \dfrac{a}{{2\sin A}}\)
Vậy ở cả hai hình ta đều có: \(R = \dfrac{a}{{2\sin A}}\).
Trong mỗi hình dưới dây, hãy tính R theo a và sinA.
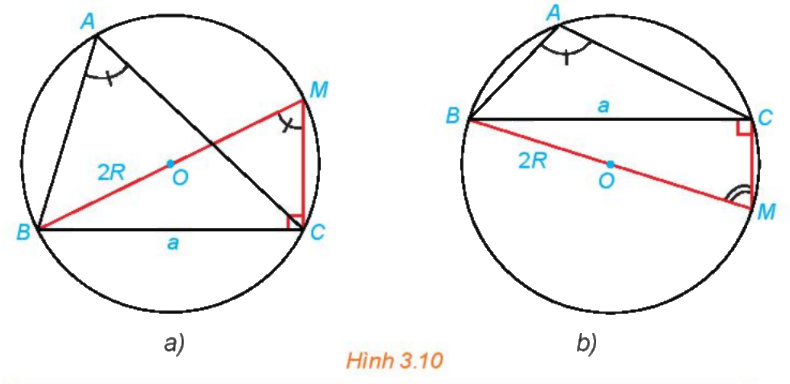
Phương pháp giải:
Bước 1: Tính sin M. Từ đó tính R theo a và sinM.
Bước 2: Tìm mối liên hệ giữa sinA và sinM, suy ra công thức tính R theo sinA.
Lời giải chi tiết:
Xét tam giác MBC vuông tại C ta có:
\(\sin M = \dfrac{{BC}}{{BM}} = \dfrac{a}{{2R}} \Rightarrow R = \dfrac{a}{{2\sin M}}\)
Lại có: Hình 3.10 a: \(\widehat A = \widehat M\) (cùng chắn cung nhỏ BC )
\( \Rightarrow \sin A = \sin M \Rightarrow R = \dfrac{a}{{2\sin A}}\)
Hình 3.10b: \(\widehat A + \widehat M = {180^o}\) (cùng tứ giác ABMC nội tiếp đường tròn (O,R))
\( \Rightarrow \sin A = \sin M \Rightarrow R = \dfrac{a}{{2\sin A}}\)
Vậy ở cả hai hình ta đều có: \(R = \dfrac{a}{{2\sin A}}\).
Cho tam giác ABC có b = 8, c = 5 và \(\widehat B = {80^o}\). Tính số đo các góc, bán kính đường tròn ngoại tiếp và độ dài cạnh còn lại của tam giác.
Phương pháp giải:
Bước 1: Tính sin\(\widehat C\), bằng cách áp dụng định lí sin tại đỉnh B và C. Từ đó suy ra số đo góc C.
Bước 2: Tính \(\widehat A\) và suy ra a dựa vào định lí sin.
Bước 3: Tính R.
Lời giải chi tiết:
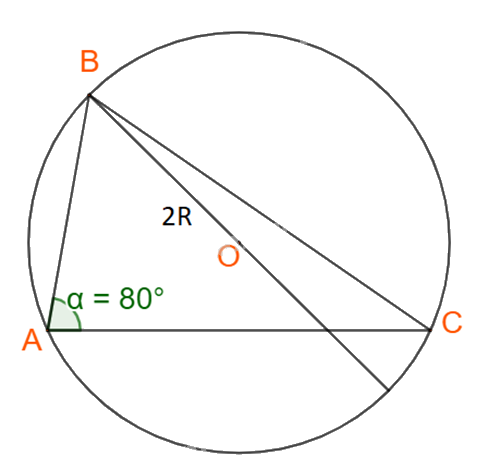
Áp dụng định lí sin cho tam giác ABC ta có:
\(\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}} = 2R\)
\(\begin{array}{l} \Rightarrow \sin C = \frac{{c.\sin B}}{b} = \frac{{5.\sin {{80}^o}}}{8} \approx 0,6155\\ \Leftrightarrow \widehat C \approx {38^o}\end{array}\)
Lại có: \(\widehat A = {180^o} - \widehat B - \widehat C = {180^o} - {80^o} - {38^o} = {62^o}\)
Theo định lí sin, ta suy ra \(a = \sin A.\dfrac{b}{{\sin B}} = \sin {62^o}\dfrac{8}{{\sin {{80}^o}}} \approx 7,17\)
Và \(2R = \dfrac{b}{{\sin B}} \Rightarrow R = \dfrac{b}{{2\sin B}} = \dfrac{8}{{2\sin {{80}^o}}} \approx 4,062.\)
Vậy tam giác ABC có \(\widehat A = {62^o}\); \(\widehat C \approx {38^o}\); \(a \approx 7,17\) và \(R \approx 4,062.\)
Mục 2 của chương trình Toán 10 tập 1 Kết nối tri thức tập trung vào các khái niệm cơ bản về tập hợp số, bao gồm tập số thực, các phép toán trên tập số thực, và các tính chất của chúng. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương trình Toán học ở các lớp trên.
Mục 2 trang 39, 40 SGK Toán 10 tập 1 Kết nối tri thức bao gồm các bài tập rèn luyện về:
Để xác định một số thuộc tập hợp nào, ta cần dựa vào định nghĩa của từng tập hợp. Ví dụ:
Khi thực hiện các phép toán trên tập số thực, ta cần tuân thủ các quy tắc về thứ tự thực hiện phép toán (nhân, chia trước; cộng, trừ sau). Ví dụ:
2 + 3 * 4 = 2 + 12 = 14
Để đơn giản biểu thức, ta có thể sử dụng các tính chất giao hoán, kết hợp, phân phối của phép toán. Ví dụ:
2(x + 3) = 2x + 6
Giá trị tuyệt đối của một số thực là khoảng cách từ số đó đến 0 trên trục số. Ví dụ:
| -5 | = 5
| 3 | = 3
Ngoài sách giáo khoa, các em có thể tham khảo thêm các tài liệu sau để học tốt Toán 10:
Hy vọng với lời giải chi tiết và những lưu ý trên, các em học sinh sẽ tự tin hơn khi giải các bài tập trong mục 2 trang 39, 40 SGK Toán 10 tập 1 Kết nối tri thức. Chúc các em học tốt!