Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 trang 52, 53, 54 sách giáo khoa Toán 10 tập 1 chương trình Kết nối tri thức.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và tự tin hơn trong học tập.
Thế nào là hai lực cân bằng? Nếu dùng hai vectơ để biểu diễn hai lực cần bằng thì hai vectơ này có mối quan hệ gì với nhau? Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD và O là trung điểm của MN. Tính lực kéo cần thiết để kéo một khẩu pháo có trọng lượng 22 148 N (ứng với khối lượng xấp xỉ 2 260kg) lên một con dốc nghiêng
Thế nào là hai lực cân bằng? Nếu dùng hai vectơ để biểu diễn hai lực cần bằng thì hai vectơ này có mối quan hệ gì với nhau?
Lời giải chi tiết:
Chẳng hạn khi hai đội kéo co bất phân thắng bại.
Hai đội cùng kéo dây nhằm kéo dây về phía mình, khi lực từ hai phía bằng nhau thì điểm buộc dây gần như không dịch chuyển. Khi đó ta nói lực kéo của hai đội là cân bằng.
Vecto biểu diễn lực, thể hiện phương, chiều và độ lớn. Dễ thấy hai lực này ngược hướng (cùng phương, ngược chiều) và có chung điểm đầu là điểm cân bằng, độ lớn như nhau.

Vậy hai lực cân bằng là hai lực mà khi tác dụng đồng thời vào 1 điểm (hay vật) thì điểm (vật) đó không di chuyển.
Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD và O là trung điểm của MN. Chứng minh rằng: \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 .\)
Phương pháp giải:
Nếu I là trung điểm của AB thì \(\overrightarrow {IA} + \;\overrightarrow {IB} = \;\overrightarrow 0 \).
Lời giải chi tiết:
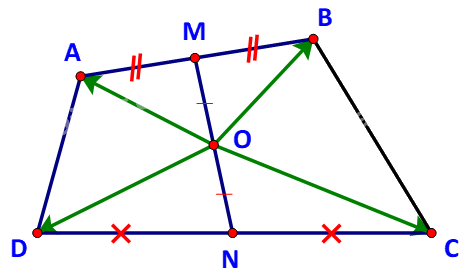
Dễ thấy: \(\overrightarrow {OA} = \overrightarrow {OM} + \overrightarrow {MA} \); \(\overrightarrow {OB} = \overrightarrow {OM} + \overrightarrow {MB} \)
Tương tự: \(\overrightarrow {OC} = \overrightarrow {ON} + \overrightarrow {NC} \); \(\overrightarrow {OD} = \overrightarrow {ON} + \overrightarrow {ND} \)
\(\begin{array}{l} \Rightarrow \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \left( {\overrightarrow {OM} + \overrightarrow {MA} } \right) + \left( {\overrightarrow {OM} + \overrightarrow {MB} } \right) + \left( {\overrightarrow {ON} + \overrightarrow {NC} } \right) + \left( {\overrightarrow {ON} + \overrightarrow {ND} } \right)\\ = \left( {\overrightarrow {OM} + \overrightarrow {OM} + \overrightarrow {MA} + \overrightarrow {MB} } \right) + \left( {\overrightarrow {ON} + \overrightarrow {ON} + \overrightarrow {NC} + \overrightarrow {ND} } \right)\\ = \overrightarrow {OM} + \overrightarrow {OM} + \overrightarrow {ON} + \overrightarrow {ON} \\ = \left( {\overrightarrow {OM} + \overrightarrow {ON} } \right) + \left( {\overrightarrow {OM} + \overrightarrow {ON} } \right)\\ = \overrightarrow 0 + \overrightarrow 0 \\ = \overrightarrow 0 .\end{array}\)
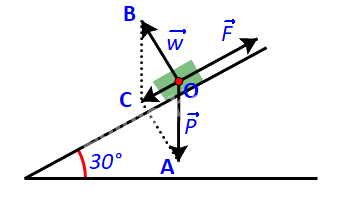
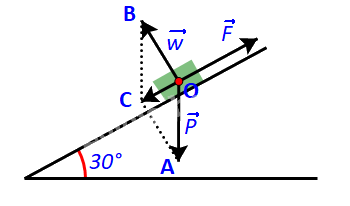
Tính lực kéo cần thiết để kéo một khẩu pháo có trọng lượng 22 148 N (ứng với khối lượng xấp xỉ 2 260kg) lên một con dốc nghiêng \({30^o}\) so với phương nằm ngang (H.4.18). Nếu lực kéo của mỗi người bằng 100N, thì cần tối thiểu bao nhiêu người để kéo pháo?
Phương pháp giải:
Khi cân bằng lực (trọng lực, phản lực, lực kéo) thì khẩu pháo đứng yên, do đó để kéo được khẩu pháo lên thì lực kéo phải lớn hơn hoặc bằng tổng hợp lực của trọng lực và phản lực.
Tìm hướng và độ lớn của tổng hợp lực giữa trọng lực và phản lực, từ đó suy ra độ lớn của lực kéo.
Lời giải chi tiết:
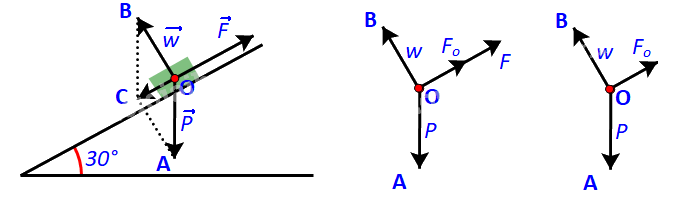
Khẩu pháo chịu tác động của ba lực: trọng lực \(\overrightarrow P \)(kí hiệu \(\overrightarrow {OA} \)), phản lực \(\overrightarrow w \)(kí hiệu \(\overrightarrow {OB} \)) và lực kéo \(\overrightarrow F \). Để kéo pháo thì độ lớn của lực kéo phải lớn hơn độ lớn của lực kéo khi pháo cân bằng \(\overrightarrow {{F_o}} \)(kí hiệu \(\overrightarrow {O{F_o}} \) )
Khi pháo cân bằng thì: \(\overrightarrow P + \overrightarrow w + \overrightarrow {{F_o}} = \overrightarrow 0 \)
Để tổng hợp lực \(\overrightarrow P \) và \(\overrightarrow w \), ta vẽ hình bình hành OACB.
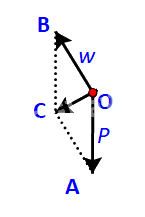
Ta có:
\(OB = \;AC;\;\;OB//\;AC\;\; \Rightarrow \overrightarrow {OB} = \;\overrightarrow {AC} \)
\( \Rightarrow \overrightarrow {OB} + \overrightarrow {OA} = \overrightarrow {AC} + \overrightarrow {OA} = \overrightarrow {OA} + \overrightarrow {AC} = \overrightarrow {OC} \)
\( \Rightarrow \overrightarrow 0 = \overrightarrow P + \overrightarrow w + \overrightarrow {{F_o}} = \overrightarrow {OB} + \overrightarrow {OA} + \overrightarrow {O{F_o}} = \overrightarrow {OC} + \overrightarrow {O{F_o}} \)
\( \Rightarrow \;O\) là trung điểm của \(C{F_o}\), hay \(OC = \left| {\overrightarrow {{F_o}} } \right|\).
Lại có: \(OB \bot \;\;OC\)(do \(\overrightarrow {OB} \) là phản lực)
\( \Rightarrow \;AC \bot CO \Rightarrow OC = OA\,.\,\,\cos \widehat {AOC}\)
Mà \(\widehat {AOC} = {90^o} - {30^o} = {60^o}\); \(\left| {\overrightarrow P } \right| = OA = 22\;148\;N\)
\( \Rightarrow OC = 22\;148\,.\,\,\cos {60^o} = 11074\;\left( N \right)\)
Vậy lực \(\overrightarrow {{F_o}} \)có độ lớn là \(11\;074\;N\), để kéo pháo thì lực \(\overrightarrow F \) cùng hướng với \(\overrightarrow {{F_o}} \) và \(\left| {\overrightarrow F } \right| > 11\;074\;N\)
Vì \(11\;074\;:100 = 110,74\) nên cần tối thiểu 111 người để kéo pháo.
Thế nào là hai lực cân bằng? Nếu dùng hai vectơ để biểu diễn hai lực cần bằng thì hai vectơ này có mối quan hệ gì với nhau?
Lời giải chi tiết:
Chẳng hạn khi hai đội kéo co bất phân thắng bại.
Hai đội cùng kéo dây nhằm kéo dây về phía mình, khi lực từ hai phía bằng nhau thì điểm buộc dây gần như không dịch chuyển. Khi đó ta nói lực kéo của hai đội là cân bằng.
Vecto biểu diễn lực, thể hiện phương, chiều và độ lớn. Dễ thấy hai lực này ngược hướng (cùng phương, ngược chiều) và có chung điểm đầu là điểm cân bằng, độ lớn như nhau.

Vậy hai lực cân bằng là hai lực mà khi tác dụng đồng thời vào 1 điểm (hay vật) thì điểm (vật) đó không di chuyển.
Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD và O là trung điểm của MN. Chứng minh rằng: \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 .\)
Phương pháp giải:
Nếu I là trung điểm của AB thì \(\overrightarrow {IA} + \;\overrightarrow {IB} = \;\overrightarrow 0 \).
Lời giải chi tiết:
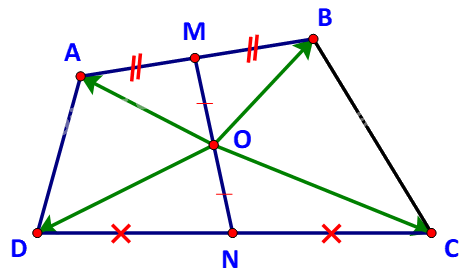
Dễ thấy: \(\overrightarrow {OA} = \overrightarrow {OM} + \overrightarrow {MA} \); \(\overrightarrow {OB} = \overrightarrow {OM} + \overrightarrow {MB} \)
Tương tự: \(\overrightarrow {OC} = \overrightarrow {ON} + \overrightarrow {NC} \); \(\overrightarrow {OD} = \overrightarrow {ON} + \overrightarrow {ND} \)
\(\begin{array}{l} \Rightarrow \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \left( {\overrightarrow {OM} + \overrightarrow {MA} } \right) + \left( {\overrightarrow {OM} + \overrightarrow {MB} } \right) + \left( {\overrightarrow {ON} + \overrightarrow {NC} } \right) + \left( {\overrightarrow {ON} + \overrightarrow {ND} } \right)\\ = \left( {\overrightarrow {OM} + \overrightarrow {OM} + \overrightarrow {MA} + \overrightarrow {MB} } \right) + \left( {\overrightarrow {ON} + \overrightarrow {ON} + \overrightarrow {NC} + \overrightarrow {ND} } \right)\\ = \overrightarrow {OM} + \overrightarrow {OM} + \overrightarrow {ON} + \overrightarrow {ON} \\ = \left( {\overrightarrow {OM} + \overrightarrow {ON} } \right) + \left( {\overrightarrow {OM} + \overrightarrow {ON} } \right)\\ = \overrightarrow 0 + \overrightarrow 0 \\ = \overrightarrow 0 .\end{array}\)
Tính lực kéo cần thiết để kéo một khẩu pháo có trọng lượng 22 148 N (ứng với khối lượng xấp xỉ 2 260kg) lên một con dốc nghiêng \({30^o}\) so với phương nằm ngang (H.4.18). Nếu lực kéo của mỗi người bằng 100N, thì cần tối thiểu bao nhiêu người để kéo pháo?
Phương pháp giải:
Khi cân bằng lực (trọng lực, phản lực, lực kéo) thì khẩu pháo đứng yên, do đó để kéo được khẩu pháo lên thì lực kéo phải lớn hơn hoặc bằng tổng hợp lực của trọng lực và phản lực.
Tìm hướng và độ lớn của tổng hợp lực giữa trọng lực và phản lực, từ đó suy ra độ lớn của lực kéo.
Lời giải chi tiết:
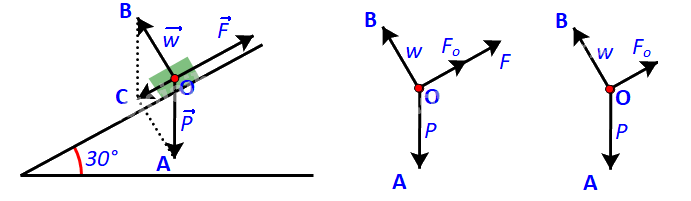
Khẩu pháo chịu tác động của ba lực: trọng lực \(\overrightarrow P \)(kí hiệu \(\overrightarrow {OA} \)), phản lực \(\overrightarrow w \)(kí hiệu \(\overrightarrow {OB} \)) và lực kéo \(\overrightarrow F \). Để kéo pháo thì độ lớn của lực kéo phải lớn hơn độ lớn của lực kéo khi pháo cân bằng \(\overrightarrow {{F_o}} \)(kí hiệu \(\overrightarrow {O{F_o}} \) )
Khi pháo cân bằng thì: \(\overrightarrow P + \overrightarrow w + \overrightarrow {{F_o}} = \overrightarrow 0 \)
Để tổng hợp lực \(\overrightarrow P \) và \(\overrightarrow w \), ta vẽ hình bình hành OACB.
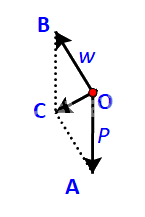
Ta có:
\(OB = \;AC;\;\;OB//\;AC\;\; \Rightarrow \overrightarrow {OB} = \;\overrightarrow {AC} \)
\( \Rightarrow \overrightarrow {OB} + \overrightarrow {OA} = \overrightarrow {AC} + \overrightarrow {OA} = \overrightarrow {OA} + \overrightarrow {AC} = \overrightarrow {OC} \)
\( \Rightarrow \overrightarrow 0 = \overrightarrow P + \overrightarrow w + \overrightarrow {{F_o}} = \overrightarrow {OB} + \overrightarrow {OA} + \overrightarrow {O{F_o}} = \overrightarrow {OC} + \overrightarrow {O{F_o}} \)
\( \Rightarrow \;O\) là trung điểm của \(C{F_o}\), hay \(OC = \left| {\overrightarrow {{F_o}} } \right|\).
Lại có: \(OB \bot \;\;OC\)(do \(\overrightarrow {OB} \) là phản lực)
\( \Rightarrow \;AC \bot CO \Rightarrow OC = OA\,.\,\,\cos \widehat {AOC}\)
Mà \(\widehat {AOC} = {90^o} - {30^o} = {60^o}\); \(\left| {\overrightarrow P } \right| = OA = 22\;148\;N\)
\( \Rightarrow OC = 22\;148\,.\,\,\cos {60^o} = 11074\;\left( N \right)\)
Vậy lực \(\overrightarrow {{F_o}} \)có độ lớn là \(11\;074\;N\), để kéo pháo thì lực \(\overrightarrow F \) cùng hướng với \(\overrightarrow {{F_o}} \) và \(\left| {\overrightarrow F } \right| > 11\;074\;N\)
Vì \(11\;074\;:100 = 110,74\) nên cần tối thiểu 111 người để kéo pháo.
Mục 2 của chương trình Toán 10 tập 1 Kết nối tri thức tập trung vào các khái niệm cơ bản về tập hợp, các phép toán trên tập hợp và các tính chất của chúng. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương trình Toán học ở các lớp trên.
Bài tập này yêu cầu học sinh xác định các tập hợp, thực hiện các phép toán hợp, giao, hiệu và phần bù của tập hợp. Đồng thời, học sinh cần chứng minh các tính chất của các phép toán này.
Bài tập này yêu cầu học sinh chứng minh các tính chất của tập hợp như tính giao hoán, tính kết hợp, tính phân phối của các phép toán hợp và giao.
Bài tập này yêu cầu học sinh sử dụng kiến thức về tập hợp để giải các bài toán thực tế.
Ví dụ 3: Trong một lớp học có 30 học sinh, có 15 học sinh thích môn Toán, 12 học sinh thích môn Văn và 8 học sinh thích cả hai môn. Hỏi có bao nhiêu học sinh không thích môn nào?
Hướng dẫn: Sử dụng công thức số phần tử của hợp hai tập hợp để giải bài toán.
Để giải tốt các bài tập về tập hợp, học sinh cần:
Khi giải bài tập về tập hợp, học sinh cần chú ý:
Hy vọng với lời giải chi tiết và hướng dẫn giải bài tập trong mục 2 trang 52, 53, 54 SGK Toán 10 tập 1 - Kết nối tri thức, các em học sinh sẽ tự tin hơn trong việc học tập môn Toán. Chúc các em học tốt!
| Công thức | Mô tả |
|---|---|
| A ∪ B | Tập hợp chứa tất cả các phần tử thuộc A hoặc B. |
| A ∩ B | Tập hợp chứa tất cả các phần tử thuộc cả A và B. |
| A \ B | Tập hợp chứa tất cả các phần tử thuộc A nhưng không thuộc B. |
| |A ∪ B| = |A| + |B| - |A ∩ B| | Số phần tử của hợp hai tập hợp. |