Bài 2.14 trang 32 SGK Toán 10 tập 1 thuộc chương trình Kết nối tri thức là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ và các phép toán vectơ. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 2.14 trang 32 SGK Toán 10 tập 1, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Biểu diễn miền nghiệm của hệ bất phương trình trên mặt phẳng tọa độ.
Đề bài
Biểu diễn miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}y - 2x \le 2\\y \le 4\\x \le 5\\x + y \ge - 1\end{array} \right.\) trên mặt phẳng tọa độ.
Từ đó tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(F\left( {x;y} \right) = - x - y\) với \(\left( {x;y} \right)\) thỏa mãn hệ trên.
Phương pháp giải - Xem chi tiết
- Biểu diễn các miền nghiệm của từng bất phương trình \(y - 2x \le 2\); \(y \le 4\); \(x \le 5\) và \(x + y \ge - 1\) trên cùng một mặt phẳng tọa độ.
Bước 1: Vẽ đường thẳng \(ax + by = c\)
Bước 2: Lấy điểm một điểm không thuộc đường thẳng \(ax + by = c\) và thay vào bất phương trình cần xác định miền nghiệm.
Bước 3: Nếu tọa độ điểm đó thỏa mãn bất phương trình thì miền nghiệm của bất phương trình chứa điểm đó.
- Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(F\left( {x;y} \right) = - x - y\)
Bước 1: Xác định các đỉnh của đa giác
Bước 2: Tính giá trị \(F\left( {x;y} \right) = - x - y\) tại các đỉnh đó và kết luận.
Lời giải chi tiết
Bước 1: Vẽ đường thẳng \(d_1: y-2x=2\) đi qua (0;2) và (-1;0).
Lấy điểm O(0;0) không thuộc \(d_1\). Vì 0-2.0=0<2 nên O thuộc miền nghiệm
Miền nghiệm của BPT \(y - 2x \le 2\) là nửa mp bờ \(d_1\), chứa điểm O.
Bước 2: Vẽ đường thẳng \(d_2: y=4\) đi qua (0;4) và (1;4).
Lấy điểm O(0;0) không thuộc \(d_2\). Vì 0<4 nên O thuộc miền nghiệm.
Miền nghiệm của BPT \(y \le 4\) là nửa mp bờ \(d_2\), chứa điểm O.
Bước 3: Vẽ đường thẳng \(d_3: x=5\) đi qua (5;0) và (5;1).
Lấy điểm O(0;0) không thuộc \(d_3\). Vì 0<5 nên O thuộc miền nghiệm
Miền nghiệm của BPT \(x \le 5\) là nửa mp bờ \(d_3\), chứa điểm O.
Bước 4: Vẽ đường thẳng \(d_4: x + y = - 1\) đi qua (-1;0) và (0;-1).
Lấy điểm O(0;0) không thuộc \(d_4\). Vì 0+0=0>-1 nên O thuộc miền nghiệm.
Miền nghiệm của BPT \(x + y \ge - 1\) là nửa mp bờ \(d_4\), chứa điểm O.
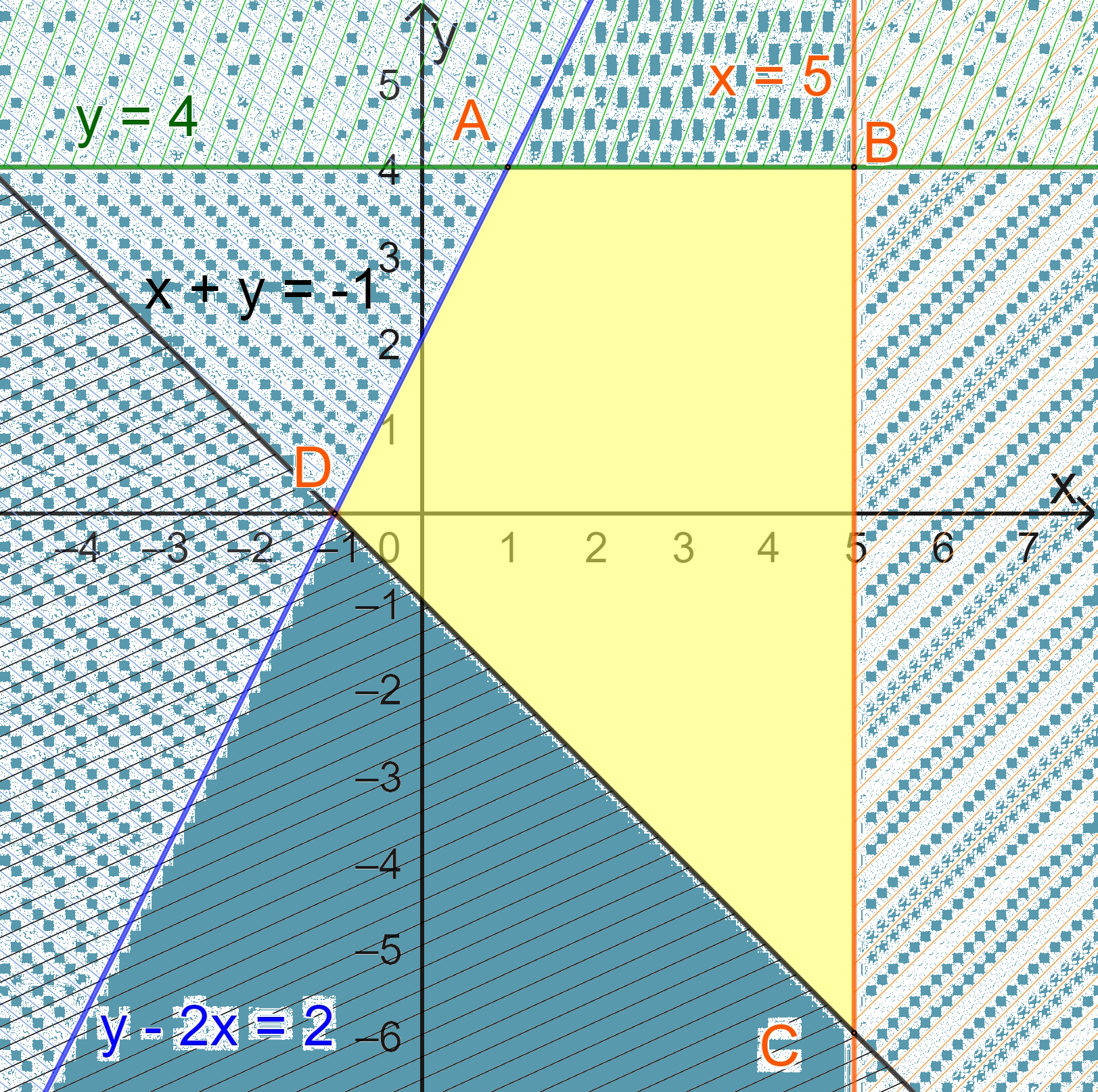
Miền biểu diễn nghiệm của hệ bất phương trình là miền tứ giác ABCD với
A(1;4); B(5;4), C(5;-6); D(-1;0).
Giá trị F tại các điểm A, B, C, D lần lượt là:
\(F\left( {1;4} \right) = - 1 - 4 = - 5\)
\(F\left( {5;4} \right) = - 5 - 4 = - 9\)
\(F\left( {5;-6} \right) = - 5 - (-6) = 1\)
\(F\left( { - 1;0} \right) = - \left( { - 1} \right) - 0 = 1\)
Vậy giá trị lớn nhất của biểu thức F(x;y) là 1 và giá trị nhỏ nhất của biểu thức F(x;y) là -9.
Trước khi đi vào giải chi tiết bài 2.14, chúng ta cùng ôn lại một số kiến thức cơ bản về vectơ và các phép toán vectơ. Vectơ là một đoạn thẳng có hướng, được xác định bởi điểm đầu và điểm cuối. Các phép toán vectơ bao gồm:
Việc nắm vững các kiến thức này là nền tảng để giải quyết bài tập 2.14 một cách hiệu quả.
Đề bài: (Nội dung đề bài sẽ được chèn vào đây - ví dụ: Cho tam giác ABC, tìm vectơ AB + AC)
Lời giải:
(Giải chi tiết từng bước của bài toán, kèm theo hình vẽ minh họa nếu cần thiết. Ví dụ:)
Ví dụ:
Áp dụng quy tắc hình bình hành, ta có: AB + AC = AD, trong đó AD là đường chéo của hình bình hành ABCD.
Do đó, vectơ AB + AC có độ dài bằng độ dài đường chéo AD và hướng từ A đến D.
Ngoài bài 2.14, còn rất nhiều bài tập tương tự về vectơ và các phép toán vectơ. Để giải quyết các bài tập này, bạn có thể áp dụng các phương pháp sau:
Để củng cố kiến thức và kỹ năng, bạn có thể tự giải các bài tập sau:
Bài 2.14 trang 32 SGK Toán 10 tập 1 – Kết nối tri thức là một bài tập quan trọng giúp học sinh nắm vững kiến thức về vectơ và các phép toán vectơ. Hy vọng với lời giải chi tiết và các phương pháp giải đã trình bày, các em học sinh sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán.
| Khái niệm | Giải thích |
|---|---|
| Vectơ | Một đoạn thẳng có hướng, xác định bởi điểm đầu và điểm cuối. |
| Phép cộng vectơ | Quy tắc hình bình hành hoặc quy tắc tam giác. |
| Tích vô hướng | a.b = |a||b|cos(θ) |