Giải bài 6.5 trang 9 SGK Toán 10 – Kết nối tri thức

Bài 6.5 trang 9 SGK Toán 10 – Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 10. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ để giải quyết các bài toán thực tế.

Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 6.5 trang 9 SGK Toán 10 – Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.

Vẽ đồ thị các hàm số sau và chỉ ra các khoảng đồng biến, nghịch biến của chúng.

Đề bài

Vẽ đồ thị các hàm số sau và chỉ ra các khoảng đồng biến, nghịch biến của chúng.

a) \(y = - 2x + 1\)

b)\(y = - \frac{1}{2}{x^2}\)

Phương pháp giải - Xem chi tiết Giải bài 6.5 trang 9 SGK Toán 10 – Kết nối tri thức 1

Vẽ hình, quan sát đồ thị hàm số trên (a;b)

Hàm số đồng biến nếu đồ thị có dạng đi lên từ trái sang phải.

Hàm số nghịch biến nếu đồ thị có dạng đi xuống từ trái sang phải.

Lời giải chi tiết

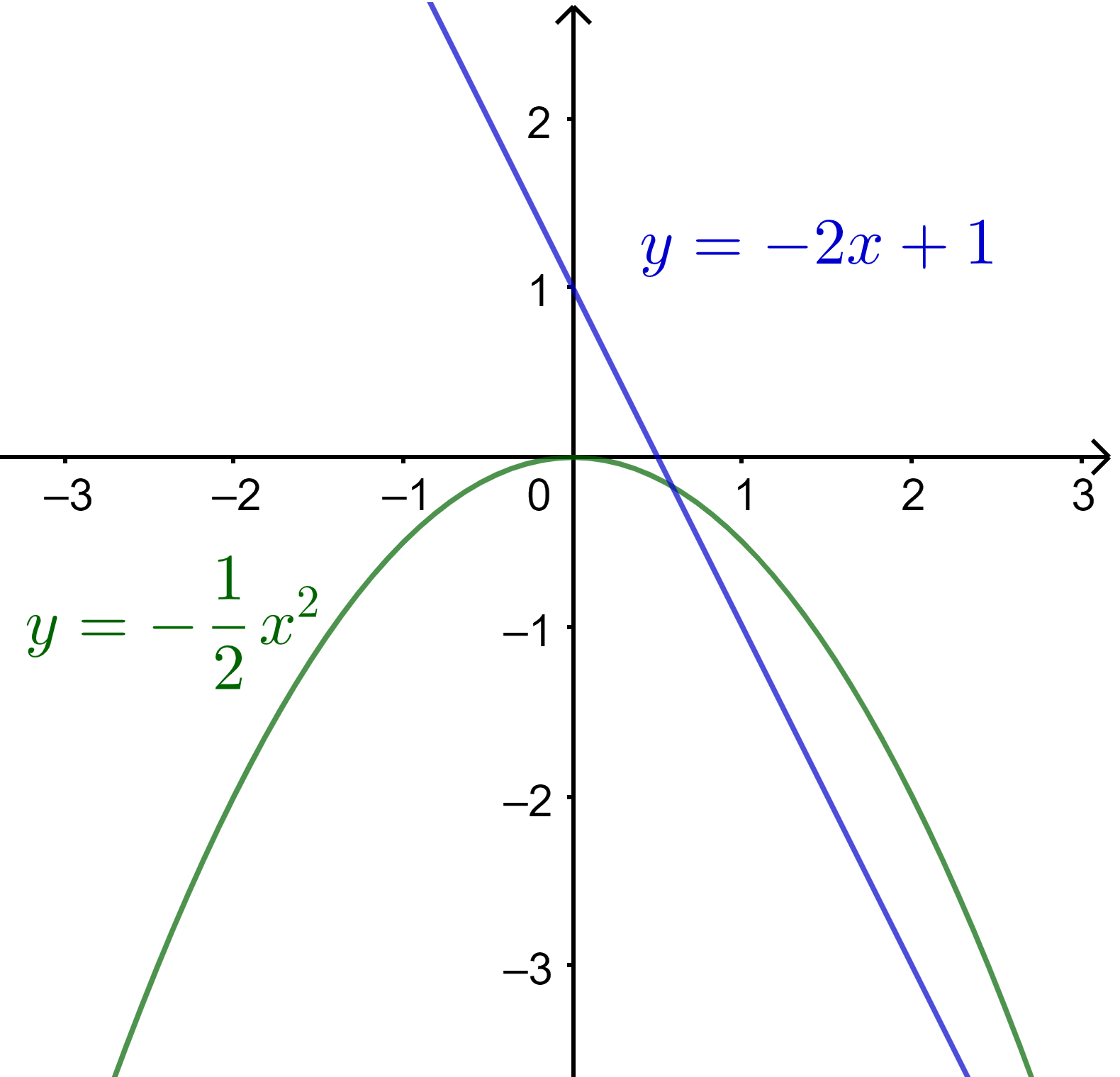
Giải bài 6.5 trang 9 SGK Toán 10 – Kết nối tri thức 2

Nhìn vào đồ thị, ta thấy:

a) Hàm số \(y = - 2x + 1\)nghịch biến trên \(\mathbb{R}\)

b) Hàm số \(y = - \frac{1}{2}{x^2}\) đồng biến trên khoảng \(\left( { - \infty ;0} \right)\); nghịch biến trên khoảng \(\left( {0; + \infty } \right)\)

Xây dựng nền tảng Toán THPT vững vàng từ hôm nay! Đừng bỏ lỡ Giải bài 6.5 trang 9 SGK Toán 10 – Kết nối tri thức đặc sắc thuộc chuyên mục giải sgk toán 10 trên nền tảng toán math. Với bộ bài tập toán trung học phổ thông được biên soạn chuyên sâu, bám sát chương trình Toán lớp 10, đây chính là "kim chỉ nam" giúp các em tối ưu hóa ôn luyện, củng cố kiến thức cốt lõi và chuẩn bị hành trang vững chắc cho tương lai. Phương pháp học trực quan, logic sẽ mang lại hiệu quả vượt trội trên lộ trình chinh phục đại học!

Giải bài 6.5 trang 9 SGK Toán 10 – Kết nối tri thức: Tóm tắt lý thuyết và phương pháp giải

Bài 6.5 trang 9 SGK Toán 10 – Kết nối tri thức thuộc chương 1: Vectơ trong mặt phẳng. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về:

Vectơ: Định nghĩa, các phép toán trên vectơ (cộng, trừ, nhân với một số).
Tọa độ của vectơ: Cách biểu diễn vectơ bằng tọa độ trong mặt phẳng.
Ứng dụng của vectơ: Giải quyết các bài toán hình học phẳng.

Nội dung bài tập 6.5 trang 9 SGK Toán 10 – Kết nối tri thức

Bài tập 6.5 yêu cầu học sinh xác định tọa độ của một điểm, cho trước tọa độ của các điểm khác và mối quan hệ vectơ giữa chúng. Cụ thể, bài tập thường có dạng:

Cho A(x_A; y_A), B(x_B; y_B). Tìm tọa độ của điểm M sao cho:

MA = kMB (với k là một số thực cho trước)
M nằm trên đường thẳng d

Phương pháp giải bài tập 6.5 trang 9 SGK Toán 10 – Kết nối tri thức

Để giải bài tập này, học sinh có thể áp dụng các bước sau:

Bước 1: Gọi tọa độ của điểm M là (x_M; y_M).
Bước 2: Biểu diễn các vectơ liên quan theo tọa độ: MA = (x_A - x_M; y_A - y_M), MB = (x_B - x_M; y_B - y_M).
Bước 3: Sử dụng điều kiện đề bài (ví dụ: MA = kMB) để thiết lập phương trình liên hệ giữa x_M và y_M.
Bước 4: Nếu M nằm trên đường thẳng d, thay phương trình đường thẳng d vào phương trình tìm được ở bước 3 để giải hệ phương trình.
Bước 5: Kiểm tra lại kết quả.

Ví dụ minh họa giải bài 6.5 trang 9 SGK Toán 10 – Kết nối tri thức

Bài tập: Cho A(1; 2), B(3; 4). Tìm tọa độ của điểm M sao cho MA = 2MB.

Giải:

Gọi M(x_M; y_M).
MA = (1 - x_M; 2 - y_M), MB = (3 - x_M; 4 - y_M).
MA = 2MB ⇔ (1 - x_M; 2 - y_M) = 2(3 - x_M; 4 - y_M)
Suy ra: 1 - x_M = 6 - 2x_M và 2 - y_M = 8 - 2y_M.
Giải hệ phương trình, ta được: x_M = 5 và y_M = 6.
Vậy M(5; 6).

Luyện tập thêm các bài tập tương tự

Để củng cố kiến thức và kỹ năng giải bài tập về vectơ, học sinh nên luyện tập thêm các bài tập tương tự trong SGK và các tài liệu tham khảo khác. Việc luyện tập thường xuyên sẽ giúp các em nắm vững kiến thức và tự tin giải quyết các bài toán khó hơn.

Giaitoan.edu.vn – Nơi học Toán hiệu quả

Giaitoan.edu.vn là một website học toán online uy tín, cung cấp lời giải chi tiết, dễ hiểu cho các bài tập Toán từ lớp 6 đến lớp 12. Chúng tôi luôn cập nhật nội dung mới nhất và cung cấp các phương pháp giải bài tập hiệu quả, giúp học sinh học Toán một cách dễ dàng và thú vị.