Bài 5.14 trang 88 SGK Toán 10 – Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 10. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học để giải quyết vấn đề.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 5.14 trang 88 SGK Toán 10 – Kết nối tri thức, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải bài tập.
Từ mẫu số liệu về thuế thuốc lá của 11 thành phố tại một quốc gia, người ta tính được: Giá trị nhỏ nhất bằng 2,5; Q1=36, Q2= 60,Q3} = 100; giá trị lớn nhất bằng 205. a) Tỉ lệ thành phố có thuế thuốc lá lớn hơn 36 là bao nhiêu? b) Chỉ ra hai giá trị sao cho có 50% giá trị của mẫu số liệu nằm giữa hai giá trị này. c) Tìm khoảng tứ phân vị của mẫu số liệu.
Đề bài
Từ mẫu số liệu về thuế thuốc lá của 51 thành phố tại một quốc gia, người ta tính được:
Giá trị nhỏ nhất bằng 2,5;\({Q_1} = 36\), \({Q_2} = 60\),\({Q_3} = 100\); giá trị lớn nhất bằng 205.
a) Tỉ lệ thành phố có thuế thuốc lá lớn hơn 36 là bao nhiêu?
b) Chỉ ra hai giá trị sao cho có 50% giá trị của mẫu số liệu nằm giữa hai giá trị này.
c) Tìm khoảng tứ phân vị của mẫu số liệu.
Phương pháp giải - Xem chi tiết
a) Các điểm \({Q_1},{Q_2},{Q_3}\) chia mẫu số liệu đã sắp xếp theo thứ tự từ nhỏ đến lớn thành 4 phần, mỗi phần chứa 25%.
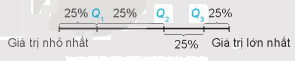
b) Lấy các giá trị sao cho tổng các khoảng là 50%
c) Khoảng tứ phân vị \({\Delta _Q} = {Q_3} - {Q_1}\)
Lời giải chi tiết
a) Tỉ lệ thành phố có thuế thuốc lá lớn hơn 36 là tỉ lệ thành phố có thuế thuốc lá lớn hơn \({Q_1}\)
=> Có 75%
b) Ta thấy từ giá trị nhỏ nhất đến \({Q_2}\) có 50% giá trị của mẫu số liệu nằm giữa hai giá trị này
=> Ta chọn giá trị thứ nhất là 2,5 và 36.
c) Khoảng tứ phân vị \({\Delta _Q} = {Q_3} - {Q_1} = 100 - 36 = 64\)
Bài 5.14 trang 88 SGK Toán 10 – Kết nối tri thức thuộc chương 4: Vectơ trong mặt phẳng. Bài tập này thường yêu cầu học sinh sử dụng các kiến thức về:
Để giải bài 5.14 trang 88 SGK Toán 10 – Kết nối tri thức một cách hiệu quả, các em cần nắm vững các kiến thức cơ bản về vectơ và các phép toán vectơ. Đồng thời, cần đọc kỹ đề bài, xác định đúng yêu cầu của bài toán và lựa chọn phương pháp giải phù hợp.
Bài 5.14 thường có dạng bài tập yêu cầu chứng minh một đẳng thức vectơ hoặc giải một bài toán hình học phẳng sử dụng vectơ. Ví dụ, bài tập có thể yêu cầu chứng minh rằng bốn điểm A, B, C, D là các đỉnh của một hình bình hành, hoặc tính độ dài của một đoạn thẳng khi biết tọa độ của các điểm đầu mút.
Để giúp các em học sinh hiểu rõ hơn về cách giải bài 5.14 trang 88 SGK Toán 10 – Kết nối tri thức, chúng ta sẽ cùng nhau phân tích một ví dụ cụ thể:
Cho tam giác ABC. Gọi M là trung điểm của BC. Chứng minh rằng: overrightarrow{AM} = (overrightarrow{AB} +overrightarrow{AC})/2
Vì M là trung điểm của BC, ta có: overrightarrow{BM} =overrightarrow{MC}.
Áp dụng quy tắc cộng vectơ, ta có: overrightarrow{AM} =overrightarrow{AB} +overrightarrow{BM}.
Thay overrightarrow{BM} =overrightarrow{MC} vào, ta được: overrightarrow{AM} =overrightarrow{AB} +overrightarrow{MC}.
Lại có: overrightarrow{AC} =overrightarrow{AM} +overrightarrow{MC}, suy ra overrightarrow{MC} =overrightarrow{AC} -overrightarrow{AM}.
Thay overrightarrow{MC} =overrightarrow{AC} -overrightarrow{AM} vào overrightarrow{AM} =overrightarrow{AB} +overrightarrow{MC}, ta được: overrightarrow{AM} =overrightarrow{AB} +overrightarrow{AC} -overrightarrow{AM}.
Chuyển vế, ta có: 2overrightarrow{AM} =overrightarrow{AB} +overrightarrow{AC}.
Suy ra: overrightarrow{AM} = (overrightarrow{AB} +overrightarrow{AC})/2 (đpcm).
Bài 5.14 trang 88 SGK Toán 10 – Kết nối tri thức là một bài tập quan trọng giúp các em học sinh củng cố kiến thức về vectơ và các phép toán vectơ. Hy vọng với lời giải chi tiết và các mẹo giải bài tập mà Giaitoan.edu.vn đã cung cấp, các em sẽ tự tin giải quyết bài tập này một cách hiệu quả.