Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 10 của giaitoan.edu.vn. Trong bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 trang 47, 48, 49, 50 sách giáo khoa Toán 10 tập 1 chương trình Kết nối tri thức.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải bài tập và tự tin hơn trong quá trình học tập môn Toán.
Quan sát các làn đường trong Hình 4.5 và cho biết những nhận xét nào sau đây là đúng. Xét các vectơ cùng phương trong Hình 4.7. Hai vectơ Cho hình thang cân ABCD với hai đấy AB, CD, AB < CD. Hãy chỉ ra mỗi quan hệ về đồ dài Trong các điều kiện dưới đây, chọn điều kiện cần và đủ để một điểm M nằm giữa hai điểm phân biệt A và B,
Xét các vectơ cùng phương trong Hình 4.7. Hai vectơ \(\overrightarrow a \) và \(\overrightarrow {AB} \)được gọi là cùng hướng, còn hai vectơ \(\overrightarrow a \) và \(\overrightarrow x \) được gọi là ngược hướng. Hãy chỉ ra các vectơ cùng hướng với vectơ \(\overrightarrow a \) và các vectơ ngược hướng với vectơ \(\overrightarrow a \).
Phương pháp giải:
Quan sát hai vectơ cùng hướng, ngược hướng chỉ ra các đặc điểm về giá và hướng (chiều) của các vectơ đó.
Lời giải chi tiết:
Hai vectơ \(\overrightarrow a \) và \(\overrightarrow {AB} \) cùng hướng: có giá song song và cùng hướng với nhau.
Hai vectơ \(\overrightarrow a \) và \(\overrightarrow x \) ngược hướng: có giá song song và ngược hướng với nhau.
Vectơ \(\overrightarrow z \) có giá song song với giá của vectơ \(\overrightarrow a \), ngược hướng với vectơ \(\overrightarrow a \) nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow z \) ngược hướng với nhau.
Vectơ \(\overrightarrow y \) có giá song song với giá của vectơ \(\overrightarrow a \), cùng hướng với vectơ \(\overrightarrow a \) nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow y \) cùng hướng với nhau.
Vectơ \(\overrightarrow b \) có giá không song song với giá của vectơ \(\overrightarrow a \) nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) không cùng phương với nhuau. Do vậy không xét chúng cùng hướng hay ngược hướng với nhau.
Quan sát các làn đường trong Hình 4.5 và cho biết những nhận xét nào sau đây là đúng.
a) Các làn đường song song với nhau.
b) Các xe chạy theo cùng một hướng
c) Hai xe bất kì đều chạy theo cùng một hướng hoặc hai hướng ngược nhau.
Phương pháp giải:
Quan sát làn đường và hướng đi chuyển (mũi tên) của các xe.
Lời giải chi tiết:
a) Các làn đường song song với nhau: Đúng.
b) Các xe chạy theo cùng một hướng: Sai.
Trong hình 4.5: Có 3 xe chạy theo hướng từ trên xuống dưới, 2 xe chạy thep hướng từ dưới lên trên
c) Hai xe bất kì đều chạy theo cùng một hướng hoặc hai hướng ngược nhau: Đúng.
Hai ca nô A và B chạy trên sông với các vận tốc riêng có cùng độ lớn là 15km/h. Tuy vậy, ca nô A chạy xuôi dòng còn ca nô B chạy ngược dòng. Vận tốc của dòng nước trên sông là 3 km/h.
a) Hãy thể hiện trên hình vẽ, vectơ vận tốc \(\overrightarrow v \) của dòng nước và các vectơ vận tốc thực tế \(\overrightarrow {{v_A}} ,\overrightarrow {{v_B}} \) của các ca nô A, B. ?
b) Trong các vectơ \(\overrightarrow v ,\overrightarrow {{v_A}} ,\overrightarrow {{v_B}} \), những cặp vectơ nào cùng phương và những cặp vectơ nào ngược hướng?
Phương pháp giải:
Vẽ 3 vectơ, lần lượt mô phỏng \(\overrightarrow v ,\overrightarrow {{v_A}} ,\overrightarrow {{v_B}} \).
Nhận xét về phương và chiều của chúng để kết luận cùng hướng hay ngược hướng.
Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.
Hai vectơ cùng phương mà cùng chiều thì được gọi là cùng hướng.
Hai vectơ cùng phương mà ngược chiều thì được gọi là ngược hướng.
Lời giải chi tiết:
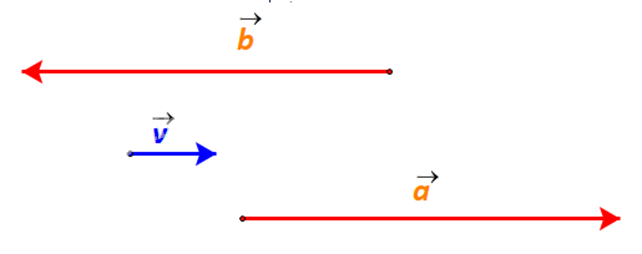
Gọi \(\overrightarrow a ,\overrightarrow b \) lần lượt là vectơ vận tốc riêng của ca nô A và B (cùng độ lớn).
Vì ca no A chạy xuôi dòng nên ngoài vận tốc riêng của ca nô, ca nô A còn được đẩy đi bởi vận tốc của dòng nước. Do đó vectơ vận tốc thực của cano A cùng hướng với vectơ \(\overrightarrow a \) và có độ lớn bằng tổng của vận tốc riêng và vận tốc dòng nước, là 18 km/h.
Ngược lại, ca nô đi ngược dòng nên bị cản lại một phần bởi dòng nước. Vì vận tốc của dòng nước nhỏ hơn vận tốc riêng của cano B nên vectơ vận tốc thực của cano B cùng hướng với vectơ \(\overrightarrow b \) và có độ lớn bằng hiệu giữa vận tốc riêng và vận tốc dòng nước, là 12 km/h.
Ta biểu diễn vận tốc thực của ca nô A và ca nô B như sau:
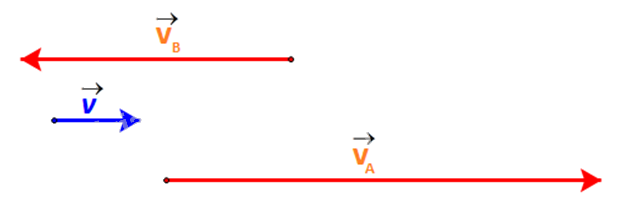
b) Dễ thấy:
Các vectơ \(\overrightarrow v ,\overrightarrow {{v_A}} ,\overrightarrow {{v_B}} \) đều có giá song song nên chúng cùng phương với nhau.
Ca nô A đi xuôi dòng nên vectơ vận tốc thực của ca nô A cùng hướng với vectơ vận tốc dòng nước.
Hay \(\overrightarrow v \) và \(\overrightarrow {{v_A}} \) cùng hướng.
Ca nô A đi ngược dòng nên vectơ vận tốc thực của ca nô B ngược hướng với vectơ vận tốc dòng nước.
Hay \(\overrightarrow v \) và \(\overrightarrow {{v_B}} \) ngược hướng.
Chú ý khi giải
Vận tốc riêng của cano là vận tốc của cano khi dòng nước đứng im.
Vận tốc thực của cano là vận tốc của cano khi kết hợp với dòng nước (đang chảy)
Trong các điều kiện dưới đây, chọn điều kiện cần và đủ để một điểm M nằm giữa hai điểm phân biệt A và B,
a) \(\overrightarrow {AB} \) và \(\overrightarrow {AM} \) ngược hướng
b) \(\overrightarrow {MA} \) và \(\overrightarrow {MB} \) cùng phương
c) \(\overrightarrow {AB} \) và \(\overrightarrow {AM} \) cùng hướng
d) \(\overrightarrow {MA} \) và \(\overrightarrow {MB} \) ngược hướng
Phương pháp giải:
Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.
Hai vectơ cùng phương mà cùng chiều thì được gọi là cùng hướng.
Hai vectơ cùng phương mà ngược chiều thì được gọi là ngược hướng.
Nhận xét: các cặp vectơ đều có cùng điểm đầu nên giá của chung song song khi và chỉ khi 3 điểm đó thẳng hàng.
Lời giải chi tiết:
a) \(\overrightarrow {AB} \) và \(\overrightarrow {AM} \) ngược hướng

\( \Leftrightarrow \left\{ \begin{array}{l}AB//AM\\B \; \text {và}\; M \; \text {nằm cùng phía so với điểm A}\end{array} \right.\)
\( \Leftrightarrow \) A, B, thẳng hàng và A nằm giữa B và M
b) \(\overrightarrow {MA} \) và \(\overrightarrow {MB} \) cùng phương
TH1: \(MA < MB\)
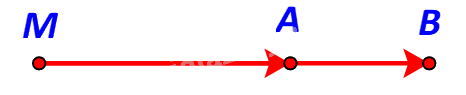
M, A, B thẳng hàng & A nằm giữa M và B.
TH2: \(MA > MB\)

M, A, B thẳng hàng & B nằm giữa M và A.
c) \(\overrightarrow {AB} \) và \(\overrightarrow {AM} \) cùng hướng
TH1: \(AM < AB\)

A, M, B thẳng hàng & M nằm giữa A và B.
TH2: \(AB < AM\)

A, M, B thẳng hàng & B nằm giữa A và M.
d) \(\overrightarrow {MA} \) và \(\overrightarrow {MB} \) ngược hướng

\( \Leftrightarrow \left\{ \begin{array}{l}MA//MB\\A \; \text {và} \; B\; \text {nằm về hai phía so với điểm M}\end{array} \right.\)
\( \Leftrightarrow \) A, M, B thẳng hàng & M nằm giữa A và B.
Vậy điều kiện cần và đủ để M nằm giữa A và B là d) \(\overrightarrow {MA} \) và \(\overrightarrow {MB} \) ngược hướng
Cho hình thang cân ABCD với hai đáy AB, CD, \(AB < CD\). Hãy chỉ ra mối quan hệ về độ dài, phương, hướng giữa các cặp vectơ \(\overrightarrow {AD} \) và \(\overrightarrow {BC} \), \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \), \(\overrightarrow {AC} \) và \(\overrightarrow {BD} \). Có cặp vectơ nào trong các cặp vectơ trên bằng nhau hay không?

Phương pháp giải:
Hai vectơ được gọi là bằng nhau nếu chúng có cùng độ dài và cùng hướng.
(Cùng hướng tức là giá của chúng song song và cùng chiều với nhau).
Lời giải chi tiết:
Xét cặp \(\overrightarrow {AD} \) và \(\overrightarrow {BC} \).
+ Độ dài: AD = BC.
+ \(\overrightarrow {AD} \) không cùng phương với \(\overrightarrow {BC} \).
+ \(\overrightarrow {AD} \) không cùng hướng với \(\overrightarrow {BC} \).
Vậy \(\overrightarrow {AD} \) không bằng \(\overrightarrow {BC} \).
Xét cặp \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \).
+ Độ dài: AB \( \ne \) CD.
+ \(\overrightarrow {AB} \) cùng phương với \(\overrightarrow {CD} \).
+ \(\overrightarrow {AB} \) không cùng hướng với \(\overrightarrow {CD} \).
Vậy \(\overrightarrow {AB} \) không bằng \(\overrightarrow {CD} \).
Xét cặp \(\overrightarrow {AC} \) và \(\overrightarrow {BD} \).
+ Độ dài: AC = BD.
+ \(\overrightarrow {AC} \) không cùng phương với \(\overrightarrow {BD} \).
+ \(\overrightarrow {AC} \) không cùng hướng với \(\overrightarrow {BD} \).
Vậy \(\overrightarrow {AC} \) không bằng \(\overrightarrow {BD} \).
Kết luận: Không có cặp vecto nào bằng nhau.
Quan sát các làn đường trong Hình 4.5 và cho biết những nhận xét nào sau đây là đúng.
a) Các làn đường song song với nhau.
b) Các xe chạy theo cùng một hướng
c) Hai xe bất kì đều chạy theo cùng một hướng hoặc hai hướng ngược nhau.
Phương pháp giải:
Quan sát làn đường và hướng đi chuyển (mũi tên) của các xe.
Lời giải chi tiết:
a) Các làn đường song song với nhau: Đúng.
b) Các xe chạy theo cùng một hướng: Sai.
Trong hình 4.5: Có 3 xe chạy theo hướng từ trên xuống dưới, 2 xe chạy thep hướng từ dưới lên trên
c) Hai xe bất kì đều chạy theo cùng một hướng hoặc hai hướng ngược nhau: Đúng.
Xét các vectơ cùng phương trong Hình 4.7. Hai vectơ \(\overrightarrow a \) và \(\overrightarrow {AB} \)được gọi là cùng hướng, còn hai vectơ \(\overrightarrow a \) và \(\overrightarrow x \) được gọi là ngược hướng. Hãy chỉ ra các vectơ cùng hướng với vectơ \(\overrightarrow a \) và các vectơ ngược hướng với vectơ \(\overrightarrow a \).
Phương pháp giải:
Quan sát hai vectơ cùng hướng, ngược hướng chỉ ra các đặc điểm về giá và hướng (chiều) của các vectơ đó.
Lời giải chi tiết:
Hai vectơ \(\overrightarrow a \) và \(\overrightarrow {AB} \) cùng hướng: có giá song song và cùng hướng với nhau.
Hai vectơ \(\overrightarrow a \) và \(\overrightarrow x \) ngược hướng: có giá song song và ngược hướng với nhau.
Vectơ \(\overrightarrow z \) có giá song song với giá của vectơ \(\overrightarrow a \), ngược hướng với vectơ \(\overrightarrow a \) nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow z \) ngược hướng với nhau.
Vectơ \(\overrightarrow y \) có giá song song với giá của vectơ \(\overrightarrow a \), cùng hướng với vectơ \(\overrightarrow a \) nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow y \) cùng hướng với nhau.
Vectơ \(\overrightarrow b \) có giá không song song với giá của vectơ \(\overrightarrow a \) nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) không cùng phương với nhuau. Do vậy không xét chúng cùng hướng hay ngược hướng với nhau.
Cho hình thang cân ABCD với hai đáy AB, CD, \(AB < CD\). Hãy chỉ ra mối quan hệ về độ dài, phương, hướng giữa các cặp vectơ \(\overrightarrow {AD} \) và \(\overrightarrow {BC} \), \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \), \(\overrightarrow {AC} \) và \(\overrightarrow {BD} \). Có cặp vectơ nào trong các cặp vectơ trên bằng nhau hay không?

Phương pháp giải:
Hai vectơ được gọi là bằng nhau nếu chúng có cùng độ dài và cùng hướng.
(Cùng hướng tức là giá của chúng song song và cùng chiều với nhau).
Lời giải chi tiết:
Xét cặp \(\overrightarrow {AD} \) và \(\overrightarrow {BC} \).
+ Độ dài: AD = BC.
+ \(\overrightarrow {AD} \) không cùng phương với \(\overrightarrow {BC} \).
+ \(\overrightarrow {AD} \) không cùng hướng với \(\overrightarrow {BC} \).
Vậy \(\overrightarrow {AD} \) không bằng \(\overrightarrow {BC} \).
Xét cặp \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \).
+ Độ dài: AB \( \ne \) CD.
+ \(\overrightarrow {AB} \) cùng phương với \(\overrightarrow {CD} \).
+ \(\overrightarrow {AB} \) không cùng hướng với \(\overrightarrow {CD} \).
Vậy \(\overrightarrow {AB} \) không bằng \(\overrightarrow {CD} \).
Xét cặp \(\overrightarrow {AC} \) và \(\overrightarrow {BD} \).
+ Độ dài: AC = BD.
+ \(\overrightarrow {AC} \) không cùng phương với \(\overrightarrow {BD} \).
+ \(\overrightarrow {AC} \) không cùng hướng với \(\overrightarrow {BD} \).
Vậy \(\overrightarrow {AC} \) không bằng \(\overrightarrow {BD} \).
Kết luận: Không có cặp vecto nào bằng nhau.
Trong các điều kiện dưới đây, chọn điều kiện cần và đủ để một điểm M nằm giữa hai điểm phân biệt A và B,
a) \(\overrightarrow {AB} \) và \(\overrightarrow {AM} \) ngược hướng
b) \(\overrightarrow {MA} \) và \(\overrightarrow {MB} \) cùng phương
c) \(\overrightarrow {AB} \) và \(\overrightarrow {AM} \) cùng hướng
d) \(\overrightarrow {MA} \) và \(\overrightarrow {MB} \) ngược hướng
Phương pháp giải:
Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.
Hai vectơ cùng phương mà cùng chiều thì được gọi là cùng hướng.
Hai vectơ cùng phương mà ngược chiều thì được gọi là ngược hướng.
Nhận xét: các cặp vectơ đều có cùng điểm đầu nên giá của chung song song khi và chỉ khi 3 điểm đó thẳng hàng.
Lời giải chi tiết:
a) \(\overrightarrow {AB} \) và \(\overrightarrow {AM} \) ngược hướng

\( \Leftrightarrow \left\{ \begin{array}{l}AB//AM\\B \; \text {và}\; M \; \text {nằm cùng phía so với điểm A}\end{array} \right.\)
\( \Leftrightarrow \) A, B, thẳng hàng và A nằm giữa B và M
b) \(\overrightarrow {MA} \) và \(\overrightarrow {MB} \) cùng phương
TH1: \(MA < MB\)
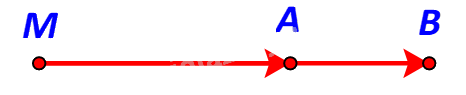
M, A, B thẳng hàng & A nằm giữa M và B.
TH2: \(MA > MB\)

M, A, B thẳng hàng & B nằm giữa M và A.
c) \(\overrightarrow {AB} \) và \(\overrightarrow {AM} \) cùng hướng
TH1: \(AM < AB\)

A, M, B thẳng hàng & M nằm giữa A và B.
TH2: \(AB < AM\)

A, M, B thẳng hàng & B nằm giữa A và M.
d) \(\overrightarrow {MA} \) và \(\overrightarrow {MB} \) ngược hướng

\( \Leftrightarrow \left\{ \begin{array}{l}MA//MB\\A \; \text {và} \; B\; \text {nằm về hai phía so với điểm M}\end{array} \right.\)
\( \Leftrightarrow \) A, M, B thẳng hàng & M nằm giữa A và B.
Vậy điều kiện cần và đủ để M nằm giữa A và B là d) \(\overrightarrow {MA} \) và \(\overrightarrow {MB} \) ngược hướng
Hai ca nô A và B chạy trên sông với các vận tốc riêng có cùng độ lớn là 15km/h. Tuy vậy, ca nô A chạy xuôi dòng còn ca nô B chạy ngược dòng. Vận tốc của dòng nước trên sông là 3 km/h.
a) Hãy thể hiện trên hình vẽ, vectơ vận tốc \(\overrightarrow v \) của dòng nước và các vectơ vận tốc thực tế \(\overrightarrow {{v_A}} ,\overrightarrow {{v_B}} \) của các ca nô A, B. ?
b) Trong các vectơ \(\overrightarrow v ,\overrightarrow {{v_A}} ,\overrightarrow {{v_B}} \), những cặp vectơ nào cùng phương và những cặp vectơ nào ngược hướng?
Phương pháp giải:
Vẽ 3 vectơ, lần lượt mô phỏng \(\overrightarrow v ,\overrightarrow {{v_A}} ,\overrightarrow {{v_B}} \).
Nhận xét về phương và chiều của chúng để kết luận cùng hướng hay ngược hướng.
Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.
Hai vectơ cùng phương mà cùng chiều thì được gọi là cùng hướng.
Hai vectơ cùng phương mà ngược chiều thì được gọi là ngược hướng.
Lời giải chi tiết:
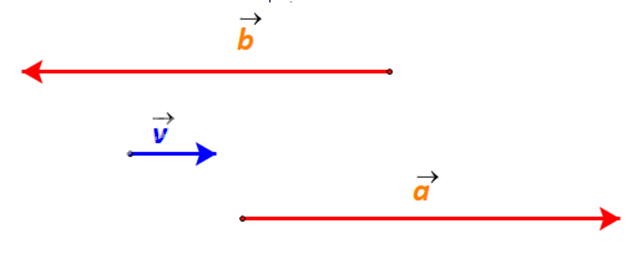
Gọi \(\overrightarrow a ,\overrightarrow b \) lần lượt là vectơ vận tốc riêng của ca nô A và B (cùng độ lớn).
Vì ca no A chạy xuôi dòng nên ngoài vận tốc riêng của ca nô, ca nô A còn được đẩy đi bởi vận tốc của dòng nước. Do đó vectơ vận tốc thực của cano A cùng hướng với vectơ \(\overrightarrow a \) và có độ lớn bằng tổng của vận tốc riêng và vận tốc dòng nước, là 18 km/h.
Ngược lại, ca nô đi ngược dòng nên bị cản lại một phần bởi dòng nước. Vì vận tốc của dòng nước nhỏ hơn vận tốc riêng của cano B nên vectơ vận tốc thực của cano B cùng hướng với vectơ \(\overrightarrow b \) và có độ lớn bằng hiệu giữa vận tốc riêng và vận tốc dòng nước, là 12 km/h.
Ta biểu diễn vận tốc thực của ca nô A và ca nô B như sau:
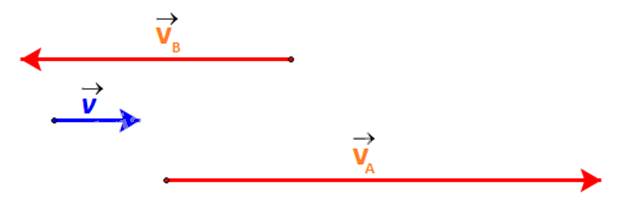
b) Dễ thấy:
Các vectơ \(\overrightarrow v ,\overrightarrow {{v_A}} ,\overrightarrow {{v_B}} \) đều có giá song song nên chúng cùng phương với nhau.
Ca nô A đi xuôi dòng nên vectơ vận tốc thực của ca nô A cùng hướng với vectơ vận tốc dòng nước.
Hay \(\overrightarrow v \) và \(\overrightarrow {{v_A}} \) cùng hướng.
Ca nô A đi ngược dòng nên vectơ vận tốc thực của ca nô B ngược hướng với vectơ vận tốc dòng nước.
Hay \(\overrightarrow v \) và \(\overrightarrow {{v_B}} \) ngược hướng.
Chú ý khi giải
Vận tốc riêng của cano là vận tốc của cano khi dòng nước đứng im.
Vận tốc thực của cano là vận tốc của cano khi kết hợp với dòng nước (đang chảy)
Mục 2 của SGK Toán 10 tập 1 Kết nối tri thức tập trung vào các kiến thức cơ bản về tập hợp số, bao gồm số thực, các phép toán trên số thực, và các tính chất của chúng. Việc nắm vững các khái niệm này là nền tảng quan trọng để học tốt các chương trình Toán học ở các lớp trên.
Để giải tốt các bài tập trong mục 2, các em cần:
Bài 1: ... (Giải chi tiết bài 1 với các bước giải rõ ràng, sử dụng các công thức và tính chất đã học)
Bài 2: ... (Giải chi tiết bài 2 với các bước giải rõ ràng, sử dụng các công thức và tính chất đã học)
Bài 3: ... (Giải chi tiết bài 3 với các bước giải rõ ràng, sử dụng các công thức và tính chất đã học)
Bài 4: ... (Giải chi tiết bài 4 với các bước giải rõ ràng, sử dụng các công thức và tính chất đã học)
Bài 5: ... (Giải chi tiết bài 5 với các bước giải rõ ràng, sử dụng các công thức và tính chất đã học)
Bài 6: ... (Giải chi tiết bài 6 với các bước giải rõ ràng, sử dụng các công thức và tính chất đã học)
Bài 7: ... (Giải chi tiết bài 7 với các bước giải rõ ràng, sử dụng các công thức và tính chất đã học)
Bài 8: ... (Giải chi tiết bài 8 với các bước giải rõ ràng, sử dụng các công thức và tính chất đã học)
Kiến thức về số thực và các phép toán trên số thực có ứng dụng rộng rãi trong nhiều lĩnh vực của đời sống, như:
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, các em có thể tham khảo thêm các bài tập tương tự trong sách bài tập Toán 10 tập 1 Kết nối tri thức hoặc trên các trang web học toán online khác.
Bài 1: Tính giá trị của biểu thức: A = (2 + √3) * (2 - √3)
Bài 2: Tìm x biết: |x - 1| = 3
Hy vọng rằng với bài viết này, các em đã nắm vững kiến thức và kỹ năng giải bài tập trong mục 2 trang 47, 48, 49, 50 SGK Toán 10 tập 1 Kết nối tri thức. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!