Chương trình Toán 10 Kết nối tri thức giới thiệu khái niệm về số gần đúng và sai số, một phần quan trọng trong việc ứng dụng toán học vào thực tế. Việc hiểu rõ các khái niệm này giúp học sinh đánh giá độ chính xác của các kết quả tính toán và đưa ra các ước lượng hợp lý.
Tại giaitoan.edu.vn, chúng tôi cung cấp tài liệu học tập đầy đủ, bài giảng chi tiết và bài tập thực hành đa dạng để giúp bạn nắm vững kiến thức về Lí thuyết Số gần đúng và sai số.
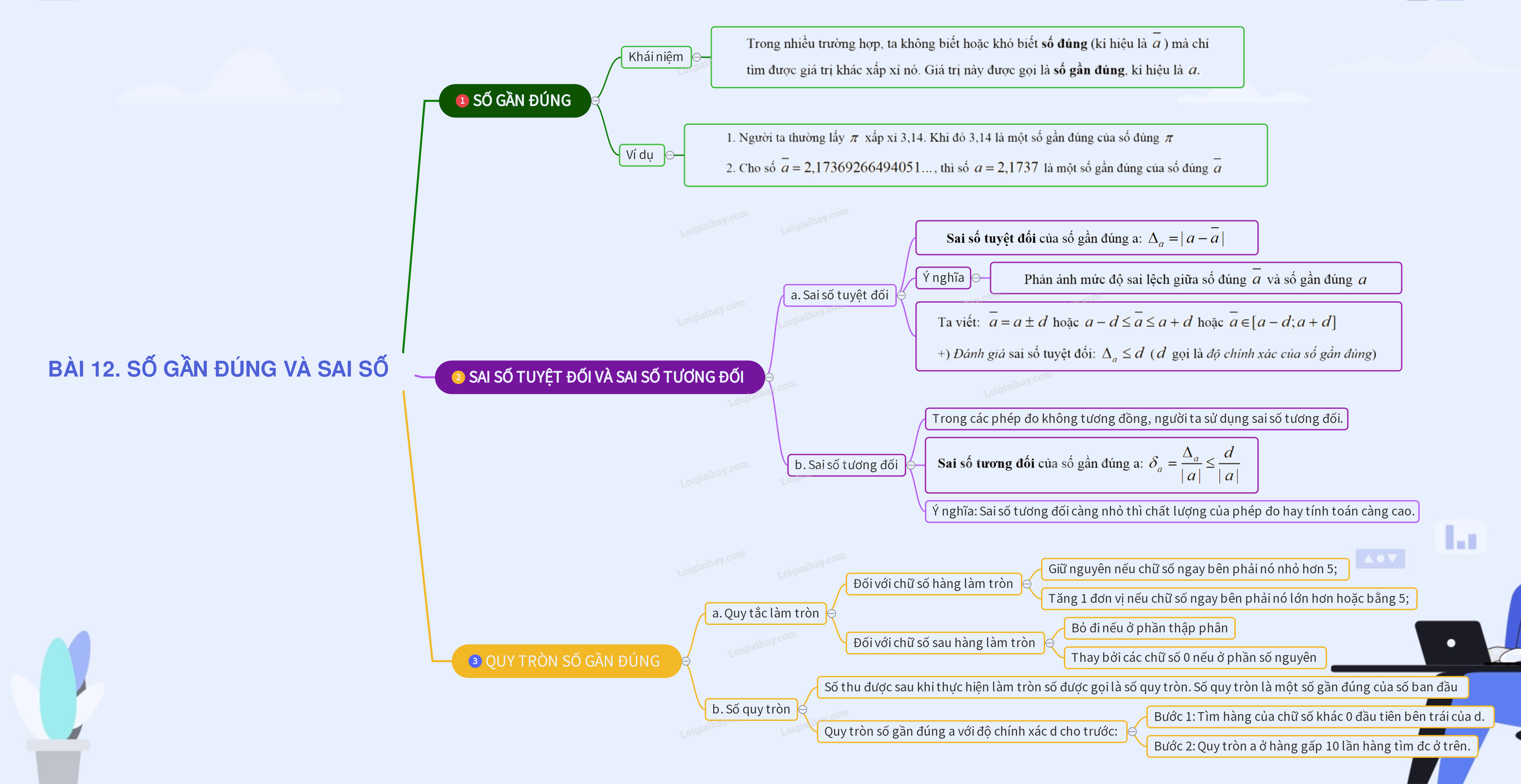
1. SỐ GẦN ĐÚNG 2. SAI SỐ TUYỆT ĐỐI VÀ SAI SỐ TƯƠNG ĐỐI 3. QUY TRÒN SỐ GẦN ĐÚNG
1. SỐ GẦN ĐÚNG
Trong nhiều trường hợp, ta không biết hoặc khó biết số đúng (kí hiệu là \(\overline a \)) mà chỉ
tìm được giá trị khác xấp xỉ nó. Giá trị này được gọi là số gần đúng, kí hiệu là \(a.\)
Ví dụ:
1. Người ta thường lấy \(\pi \) xấp xỉ 3,14. Khi đó 3,14 là một số gần đúng của số đúng \(\pi \)
2. Cho số \(\overline a = 2,17369266494051...\), thì số \(a = 2,1737\) là một số gần đúng của số đúng \(\overline a \)
2. SAI SỐ TUYỆT ĐỐI VÀ SAI SỐ TƯƠNG ĐỐI
a. Sai số tuyệt đối
+) Sai số tuyệt đối của số gần đúng a: \({\Delta _a} = \;|a - \overline a |\)
Ý nghĩa: Phản ánh mức độ sai lệch giữa số đúng \(\overline a \) và số gần đúng \(a\).
Ta viết: \(\overline a = a \pm d\) hoặc \(a - d \le \overline a \le a + d\) hoặc \(\overline a \in [a - d;a + d]\)
+) Đánh giá sai số tuyệt đối: \({\Delta _a} \le d\) (\(d\) gọi là độ chính xác của số gần đúng)
b. Sai số tương đối
Trong các phép đo không tương đồng, người ta sử dụng sai số tương đối để so sánh các phép đo.
+) Sai số tương đối của số gần đúng a: \({\delta _a} = \frac{{{\Delta _a}}}{{|a|}} \le \frac{d}{{|a|}}\)
Ý nghĩa: Sai số tương đối càng nhỏ thì chất lượng của phép đo hay tính toán càng cao.
3. QUY TRÒN SỐ GẦN ĐÚNG
a. Quy tắc làm tròn
+) Đối với chữ số hàng làm tròn:
- Giữ nguyên nếu chữ số ngay bên phải nó nhỏ hơn 5;
- Tăng 1 đơn vị nếu chữ số ngay bên phải nó lớn hơn hoặc bằng 5;
+) Đối với chữ số sau hàng làm tròn:
- Bỏ đi nếu ở phần thập phân;
- Thay bởi các chữ số 0 nếu ở phần số nguyên.
b. Số quy tròn
Số thu được sau khi thực hiện làm tròn số được gọi là số quy tròn. Số quy tròn là một số gần đúng của số ban đầu.
Quy tròn số gần đúng a với độ chính xác d cho trước:
Bước 1: Tìm hàng của chữ số khác 0 đầu tiên bên trái của d.
Bước 2: Quy tròn a ở hàng gấp 10 lần hàng tìm đc ở trên.
Trong toán học và các ứng dụng thực tế, không phải lúc nào chúng ta cũng có thể biểu diễn một số một cách chính xác tuyệt đối. Do đó, khái niệm về số gần đúng và sai số trở nên vô cùng quan trọng. Bài viết này sẽ đi sâu vào phân tích các khái niệm này theo chương trình SGK Toán 10 Kết nối tri thức.
Một số gần đúng là một giá trị được sử dụng để thay thế cho một số chính xác khi số chính xác không thể biết được hoặc không thể biểu diễn một cách dễ dàng. Ví dụ, số π (pi) là một số vô tỉ, do đó chúng ta không thể viết nó một cách chính xác. Thay vào đó, chúng ta sử dụng các giá trị gần đúng như 3.14 hoặc 3.14159.
Sai số là sự khác biệt giữa giá trị gần đúng và giá trị chính xác. Có hai loại sai số chính:
Sai số tuyệt đối cho biết độ lớn của sai số, trong khi sai số tương đối cho biết mức độ sai số so với giá trị chính xác.
Trong nhiều trường hợp, chúng ta không biết giá trị chính xác của một số. Do đó, chúng ta cần phải ước lượng sai số. Có nhiều phương pháp để ước lượng sai số, tùy thuộc vào cách chúng ta thu được giá trị gần đúng.
Ví dụ 1: Giả sử chúng ta cần tính diện tích của một hình tròn có bán kính r = 5 cm. Chúng ta sử dụng giá trị gần đúng của π là 3.14. Diện tích hình tròn được tính là A = πr2 = 3.14 * 52 = 78.5 cm2. Nếu chúng ta sử dụng giá trị chính xác của π, diện tích hình tròn sẽ là A = π * 52 ≈ 78.5398 cm2. Sai số tuyệt đối là |78.5 - 78.5398| = 0.0398 cm2, và sai số tương đối là (0.0398 / 78.5398) * 100% ≈ 0.051%.
Ví dụ 2: Khi đo chiều dài của một vật thể bằng thước đo, chúng ta luôn có sai số do độ chính xác của thước đo. Nếu thước đo có độ chia nhỏ nhất là 1 mm, thì sai số tuyệt đối tối đa là 0.5 mm.
Lí thuyết Số gần đúng và sai số có nhiều ứng dụng trong các lĩnh vực khác nhau, bao gồm:
Hãy giải các bài tập sau để củng cố kiến thức về Lí thuyết Số gần đúng và sai số:
Lí thuyết Số gần đúng và sai số là một phần quan trọng của toán học và có nhiều ứng dụng thực tế. Việc hiểu rõ các khái niệm này giúp chúng ta đánh giá độ chính xác của các kết quả tính toán và đưa ra các quyết định hợp lý. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản về chủ đề này.