Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10. Bài viết này sẽ hướng dẫn bạn giải quyết các bài tập trong mục 1 trang 47 SGK Toán 10 tập 1 - Kết nối tri thức một cách nhanh chóng và hiệu quả.
Chúng tôi cam kết cung cấp nội dung chính xác, đầy đủ và phù hợp với chương trình học Toán 10 hiện hành. Hãy cùng bắt đầu khám phá lời giải chi tiết ngay sau đây!
Một con tàu khởi hành từ đảo A, đi thẳng về hướng đông 10 km rồi đi thẳng tiếp về hướng nam thì tới đảo B (h.4.2) Cho tam giác đều ABC với cạnh có độ dài bằng a. Hãy chỉ ra các vectơ có độ dài bằng a và có điểm đầu, điểm cuối là các đỉnh của tam giác ABC.
Cho tam giác đều ABC với cạnh có độ dài bằng a. Hãy chỉ ra các vectơ có độ dài bằng a và có điểm đầu, điểm cuối là các đỉnh của tam giác ABC.
Phương pháp giải:
Nhắc lại:
+) Vectơ là một đoạn thẳng có hướng.
+) Độ dài của vectơ là độ dài đoạn thẳng ấy.
Lời giải chi tiết:
Các vectơ có độ dài bằng a và có điểm đầu, điểm cuối là các đỉnh của tam giác ABC là:
\(\overrightarrow {AB} ;\;\overrightarrow {BA} ;\;\overrightarrow {AC} ;\;\overrightarrow {CA} ;\;\overrightarrow {BC} ;\;\overrightarrow {CB} \)
Chú ý khi giải:
Vectơ \(\overrightarrow {AB} \) khác vectơ \(\overrightarrow {BA} \) (khác nhau điểm đầu và điểm cuối).
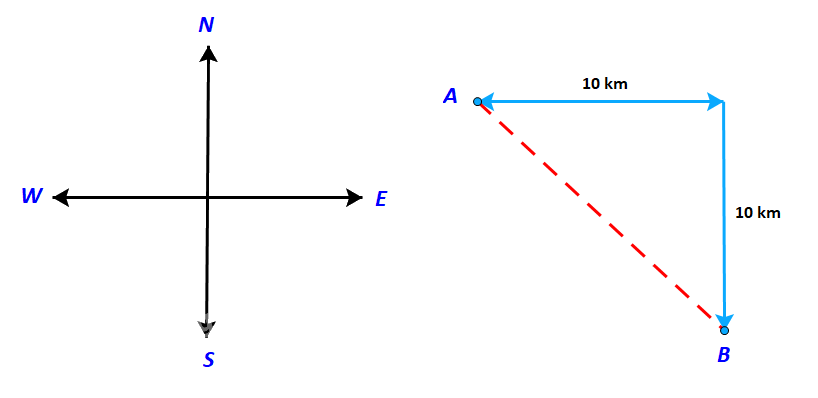
Một con tàu khởi hành từ đảo A, đi thẳng về hướng đông 10 km rồi đi thẳng tiếp về hướng nam thì tới đảo B (h.4.2). Nếu từ đảo A, tàu đi thẳng (không đổi hướng) tới đảo B, thì phải đi theo hướng nào và quãng đường phải đi dài bao nhiêu kilômét?
Phương pháp giải:
Xét tam giác, dựa vào độ dài 2 cạnh đã có để suy ra góc A.
Dựa vào định lí Pytago để tính cạnh AB
Từ đó kết luận hướng đi và quãng đường phải đi.
Lời giải chi tiết:
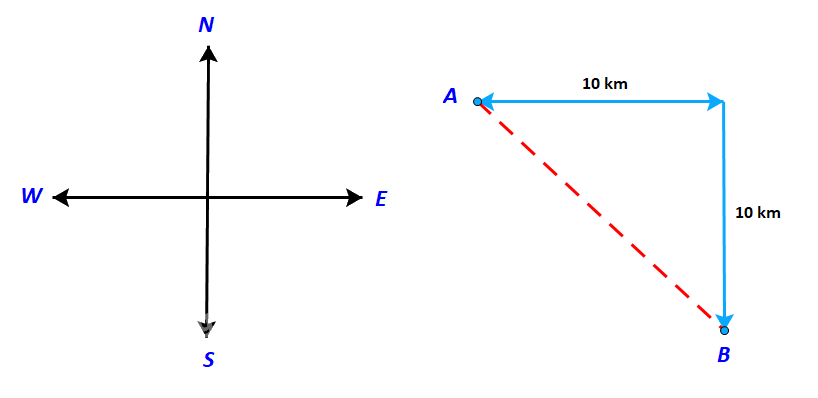
Gọi C là điểm mà tại đó tàu đổi từ hướng đông sang hướng Nam
Xét tam giác ABC ta có:
\(AC = BC = 10\;\left( {km} \right)\)
\( \Rightarrow \Delta ABC\) vuông cân tại C.
\( \Leftrightarrow \widehat A = {45^o}\)
Vậy con tàu phải đi theo hướng đông nam, góc \({45^o}\) so với hướng Đông.
Quãng đường con tàu phải đi là: \(AB = AC.\sqrt 2 = 10.\sqrt 2 \; \approx 14,142\;\left( {km} \right)\)
Cho tam giác đều ABC với cạnh có độ dài bằng a. Hãy chỉ ra các vectơ có độ dài bằng a và có điểm đầu, điểm cuối là các đỉnh của tam giác ABC.
Phương pháp giải:
Nhắc lại:
+) Vectơ là một đoạn thẳng có hướng.
+) Độ dài của vectơ là độ dài đoạn thẳng ấy.
Lời giải chi tiết:
Các vectơ có độ dài bằng a và có điểm đầu, điểm cuối là các đỉnh của tam giác ABC là:
\(\overrightarrow {AB} ;\;\overrightarrow {BA} ;\;\overrightarrow {AC} ;\;\overrightarrow {CA} ;\;\overrightarrow {BC} ;\;\overrightarrow {CB} \)
Chú ý khi giải:
Vectơ \(\overrightarrow {AB} \) khác vectơ \(\overrightarrow {BA} \) (khác nhau điểm đầu và điểm cuối).
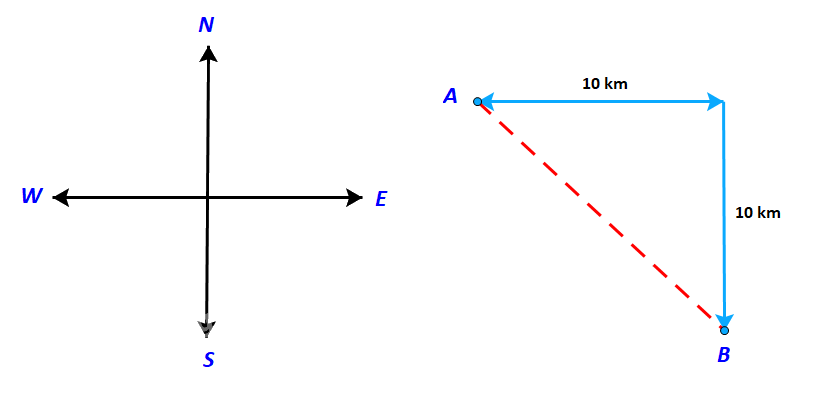
Một con tàu khởi hành từ đảo A, đi thẳng về hướng đông 10 km rồi đi thẳng tiếp về hướng nam thì tới đảo B (h.4.2). Nếu từ đảo A, tàu đi thẳng (không đổi hướng) tới đảo B, thì phải đi theo hướng nào và quãng đường phải đi dài bao nhiêu kilômét?
Phương pháp giải:
Xét tam giác, dựa vào độ dài 2 cạnh đã có để suy ra góc A.
Dựa vào định lí Pytago để tính cạnh AB
Từ đó kết luận hướng đi và quãng đường phải đi.
Lời giải chi tiết:
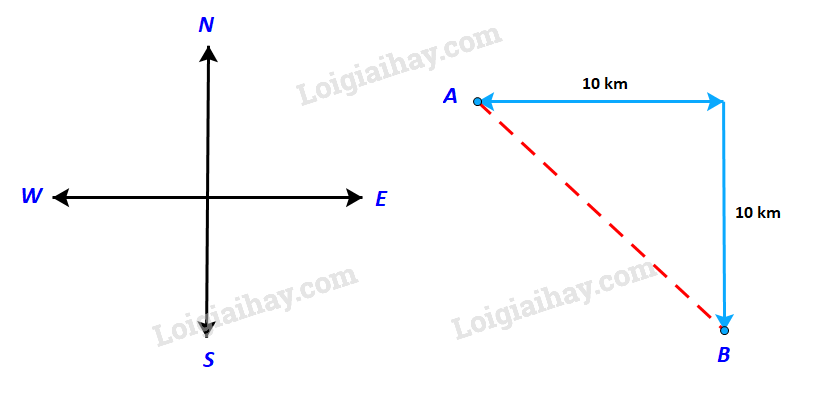
Gọi C là điểm mà tại đó tàu đổi từ hướng đông sang hướng Nam
Xét tam giác ABC ta có:
\(AC = BC = 10\;\left( {km} \right)\)
\( \Rightarrow \Delta ABC\) vuông cân tại C.
\( \Leftrightarrow \widehat A = {45^o}\)
Vậy con tàu phải đi theo hướng đông nam, góc \({45^o}\) so với hướng Đông.
Quãng đường con tàu phải đi là: \(AB = AC.\sqrt 2 = 10.\sqrt 2 \; \approx 14,142\;\left( {km} \right)\)
Mục 1 trang 47 SGK Toán 10 tập 1 - Kết nối tri thức tập trung vào việc ôn tập và củng cố kiến thức về tập hợp số, các phép toán trên tập hợp số và ứng dụng của chúng trong giải quyết các bài toán thực tế. Các bài tập trong mục này thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán về tập hợp, số thực, và các phép toán cơ bản.
Mục 1 trang 47 bao gồm một số bài tập với các mức độ khó khác nhau, từ dễ đến khó. Dưới đây là phân tích chi tiết từng bài tập:
Bài tập này yêu cầu học sinh xác định các tập hợp số như tập hợp số tự nhiên, tập hợp số nguyên, tập hợp số hữu tỉ, tập hợp số thực. Để giải bài tập này, học sinh cần nắm vững định nghĩa của từng tập hợp số và biết cách phân loại các số thuộc các tập hợp khác nhau.
Bài tập này yêu cầu học sinh thực hiện các phép toán cộng, trừ, nhân, chia trên các số thực. Để giải bài tập này, học sinh cần nắm vững các quy tắc thực hiện các phép toán trên số thực và biết cách áp dụng chúng vào giải quyết các bài toán cụ thể.
Bài tập này yêu cầu học sinh vận dụng kiến thức về tập hợp số và các phép toán trên tập hợp số để giải quyết các bài toán thực tế. Để giải bài tập này, học sinh cần biết cách phân tích bài toán, xác định các yếu tố liên quan đến tập hợp số và các phép toán, và áp dụng các kiến thức đã học để tìm ra lời giải.
Để giải các bài tập trong mục 1 trang 47 SGK Toán 10 tập 1 - Kết nối tri thức một cách hiệu quả, học sinh có thể áp dụng các phương pháp sau:
Bài tập: Cho số thực a = 2.5. Hãy xác định a thuộc tập hợp số nào?
Lời giải: Số thực a = 2.5 là một số thập phân, do đó a thuộc tập hợp số hữu tỉ và tập hợp số thực.
Khi giải các bài tập về tập hợp số, học sinh cần lưu ý:
Hy vọng rằng với những hướng dẫn chi tiết và phương pháp giải bài tập hiệu quả trên đây, bạn sẽ tự tin giải quyết các bài tập trong mục 1 trang 47 SGK Toán 10 tập 1 - Kết nối tri thức một cách nhanh chóng và chính xác. Chúc bạn học tập tốt!
| Tập hợp số | Định nghĩa | Ví dụ |
|---|---|---|
| Số tự nhiên | Các số dùng để đếm | 0, 1, 2, 3,... |
| Số nguyên | Bao gồm số tự nhiên và số âm của chúng | ..., -3, -2, -1, 0, 1, 2, 3,... |
| Số hữu tỉ | Các số có thể biểu diễn dưới dạng phân số a/b, với a, b là số nguyên và b khác 0 | 1/2, -3/4, 5,... |
| Số thực | Bao gồm số hữu tỉ và số vô tỉ | π, √2, 1.5,... |