Chào mừng các em học sinh đến với lời giải chi tiết bài 2.5 trang 30 SGK Toán 10 tập 1 – Kết nối tri thức trên giaitoan.edu.vn. Bài viết này sẽ cung cấp phương pháp giải bài tập một cách dễ hiểu, giúp các em nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất, đồng hành cùng các em trên con đường chinh phục môn Toán.
Biểu diễn miền nghiệm của mỗi hệ bất phương trình sau trên mặt phẳng tọa độ:
Đề bài
Biểu diễn miền nghiệm của mỗi hệ bất phương trình sau trên mặt phẳng tọa độ:
a) \(\left\{ \begin{array}{l}y - x < - 1\\x > 0\\y < 0\end{array} \right.\)
b) \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\2x + y \le 4\end{array} \right.\)
c) \(\left\{ \begin{array}{l}x \ge 0\\x + y > 5\\x - y < 0\end{array} \right.\)
Phương pháp giải - Xem chi tiết
Xác định miền nghiệm của từng bất phương trình bậc nhất hai ẩn.
Miền không bị gạch là miền nghiệm của hệ bất phương trình đã cho.
Lời giải chi tiết
a)
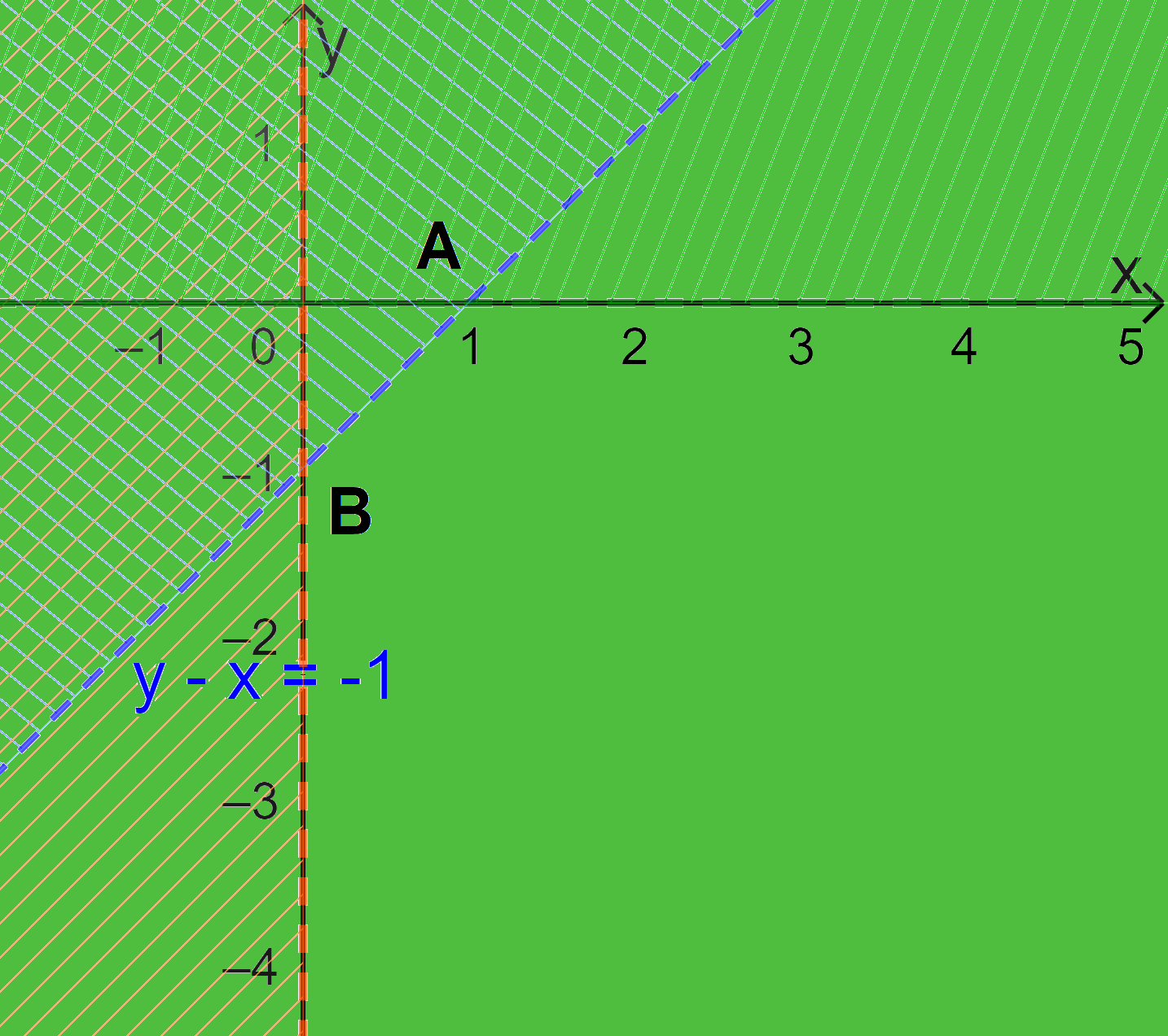
Xác định miền nghiệm của BPT \(y - x < - 1\)
+ Vẽ đường thẳng d: \(y-x= - 1\) đi qua A(1;0) và B(0;-1)
+ Vì \(0-0= 0 > - 1\) nên tọa độ điểm O(0;0) không thỏa mãn BPT \(y - x < - 1\)
Do đó, miền nghiệm của BPT \(y - x < - 1\) là nửa mặt phẳng bờ d không chứa gốc tọa độ O.
Miền nghiệm của BPT \(x > 0\) là nửa mặt phẳng bên phải Oy (không kể trục Oy).
Miền nghiệm của BPT \(y < 0\) là nửa mặt phẳng dưới Ox (không kể trục Ox).
Khi đó miền nghiệm của hệ bất phương trình đã cho là miền không gạch (Không kể đoạn thẳng AB và các trục tọa độ).
b)
Miền nghiệm của BPT \(x \ge 0\) là nửa mặt phẳng bờ Oy chứa điểm (1;0) (kể cả trục Oy).
Miền nghiệm của BPT \(y \ge 0\) là nửa mặt phẳng bờ Ox chứa điểm (0;1) (kể cả trục Ox).
Xác định miền nghiệm của bất phương trình \(2x + y \le 4\)
+ Vẽ đường thẳng d: \(2x + y = 4\) đi qua A(2;0) và B(0;4)
+ Vì \(2.0 + 0 = 0 < 4\) nên tọa độ điểm O(0;0) thỏa mãn BPT \(2x + y \le 4\)
Do đó, miền nghiệm của bất phương trình \(2x + y \le 4\) là nửa mặt phẳng bờ d chứa gốc tọa độ O.
Vậy miền nghiệm của hệ bất phương trình đã cho là miền tam giác OAB (kể cả các đoạn thẳng OA, OB, AB).
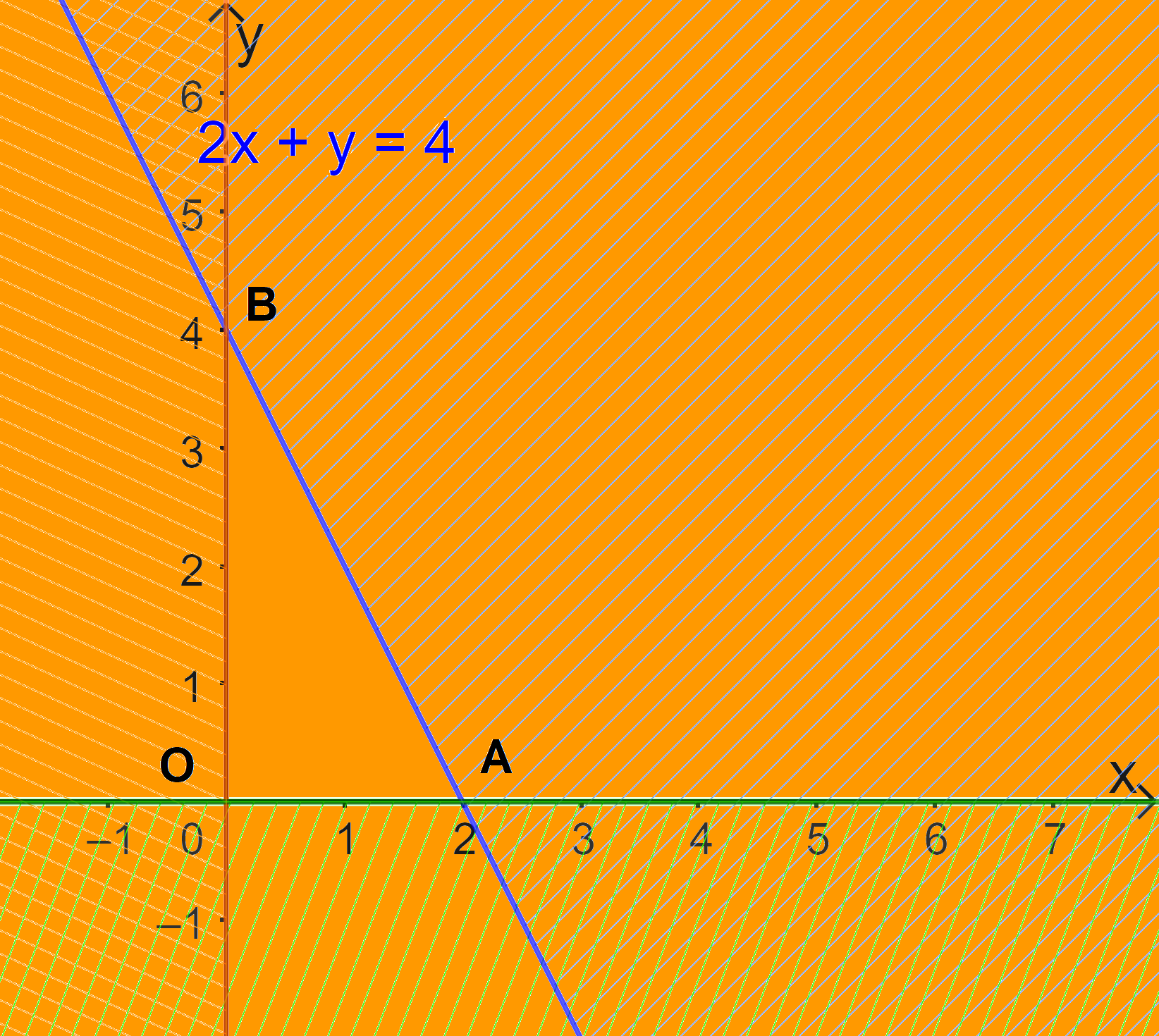
c)
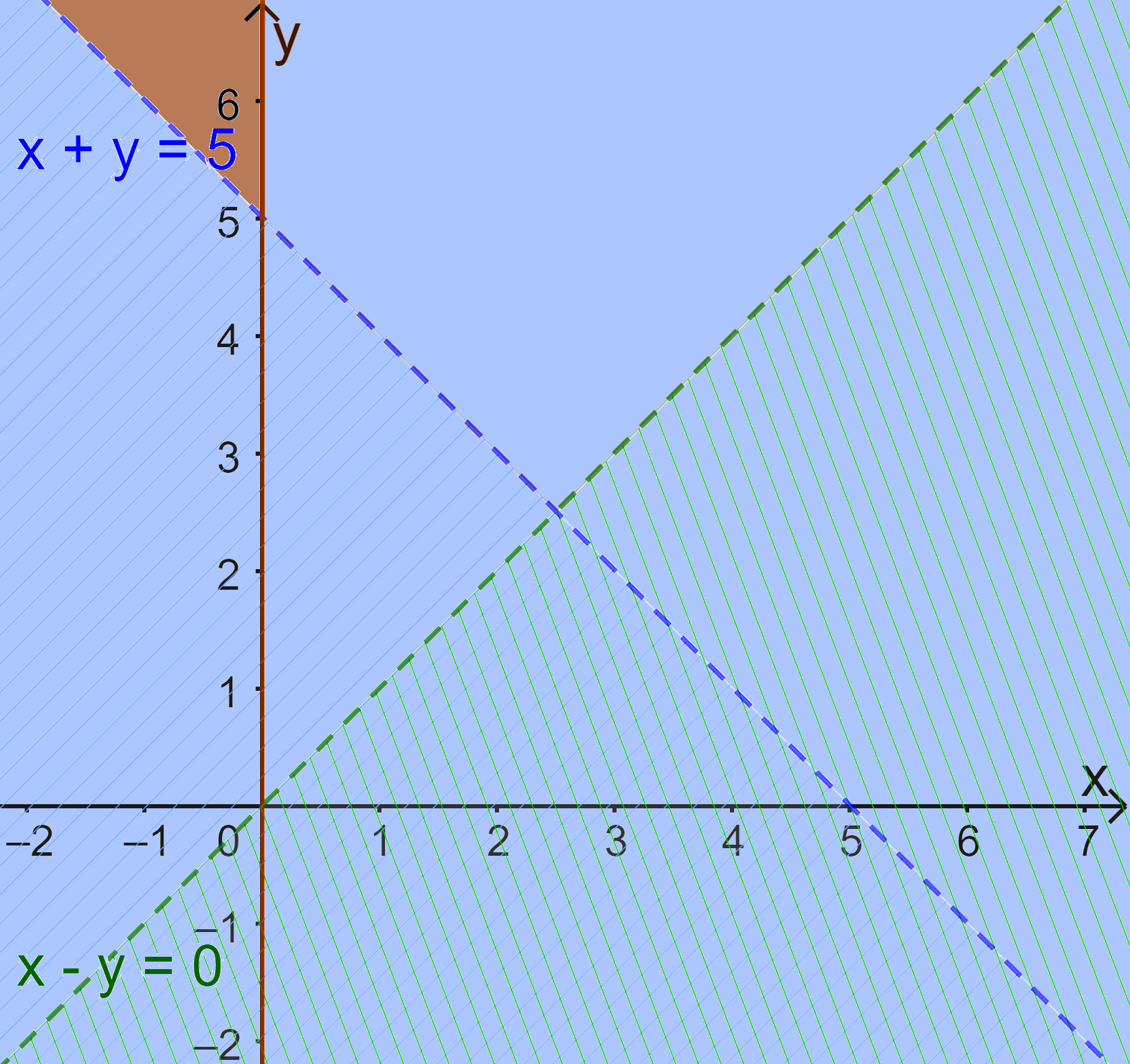
Miền nghiệm của bất phương trình \(x \ge 0\) là nửa mặt phẳng bên phải Oy (kể cả trục Oy).
Xác định miền nghiệm của bất phương trình \(x + y > 5\)
+ Vẽ đường thẳng d: \(x + y = 5\)
+ Vì \(0 + 0 = 0 < 5\) nên tọa độ điểm O(0;0) không thỏa mãn bất phương trình \(x + y > 5\).
Do đó, miền nghiệm của BPT \(x + y > 5\) là nửa mặt phẳng bờ d không chứa gốc tọa độ O.
Xác định miền nghiệm của bất phương trình \(x - y < 0\)
+ Vẽ đường thẳng d: \(x - y = 0\)
+ Vì \(1 - 0 = 1 > 0\) nên tọa độ điểm (1;0) không thỏa mãn bất phương trình \(x - y < 0\)
Do đó, miền nghiệm của bất phương trình \(x - y < 0\) là nửa mặt phẳng bờ d’ không chứa điểm (1;0).
Vậy miền nghiệm của hệ bất phương trình đã cho là miền màu trắng (không kể d và d’)
Bài 2.5 trang 30 SGK Toán 10 tập 1 – Kết nối tri thức thuộc chương 1: Mệnh đề và tập hợp. Bài tập này yêu cầu học sinh vận dụng kiến thức về tập hợp, các phép toán trên tập hợp (hợp, giao, hiệu, phần bù) để giải quyết các bài toán cụ thể. Việc hiểu rõ các khái niệm và tính chất của tập hợp là nền tảng quan trọng để giải quyết bài tập này một cách hiệu quả.
Bài tập 2.5 bao gồm một số câu hỏi nhỏ, yêu cầu học sinh:
Đề bài: Cho A = {1; 2; 3; 4; 5} và B = {3; 4; 6; 7}. Tìm A ∪ B.
Lời giải: A ∪ B là tập hợp chứa tất cả các phần tử thuộc A hoặc B (hoặc cả hai). Do đó, A ∪ B = {1; 2; 3; 4; 5; 6; 7}.
Đề bài: Cho A = {1; 2; 3; 4; 5} và B = {3; 4; 6; 7}. Tìm A ∩ B.
Lời giải: A ∩ B là tập hợp chứa tất cả các phần tử thuộc cả A và B. Do đó, A ∩ B = {3; 4}.
Đề bài: Cho A = {1; 2; 3; 4; 5} và B = {3; 4; 6; 7}. Tìm A \ B.
Lời giải: A \ B là tập hợp chứa tất cả các phần tử thuộc A nhưng không thuộc B. Do đó, A \ B = {1; 2; 5}.
Đề bài: Cho A = {1; 2; 3; 4; 5} và B = {3; 4; 6; 7}. Tìm B \ A.
Lời giải: B \ A là tập hợp chứa tất cả các phần tử thuộc B nhưng không thuộc A. Do đó, B \ A = {6; 7}.
Để củng cố kiến thức về tập hợp, các em có thể tự giải các bài tập tương tự sau:
Bài 2.5 trang 30 SGK Toán 10 tập 1 – Kết nối tri thức là một bài tập cơ bản về tập hợp. Việc nắm vững kiến thức về tập hợp và các phép toán trên tập hợp là rất quan trọng để giải quyết bài tập này một cách hiệu quả. Hy vọng rằng, với lời giải chi tiết và phương pháp giải bài tập được trình bày trong bài viết này, các em sẽ tự tin hơn trong quá trình học tập môn Toán.