Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9 tập 2. Bài viết này sẽ hướng dẫn bạn giải bài tập 1 trang 46 SGK Toán 9 tập 2 - Chân trời sáng tạo một cách nhanh chóng và hiệu quả.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức. Vì vậy, chúng tôi luôn cố gắng cung cấp những lời giải rõ ràng, chi tiết, kèm theo các giải thích cụ thể để bạn có thể hiểu rõ bản chất của bài toán.
Bạn Giang ghi lại cự li nhảy xa của các bạn trong câu lạc bộ thể thao ở bảng sau (đơn vị: mét) a) Để thu gọn bảng dữ liệu thì nên chọn bảng tần số không ghép nhóm hay bảng tần số ghép nhóm để biểu thị dữ liệu trên? Tại sao? b) Hãy chia số liệu thành 4 nhóm, trong đó nhóm đầu tiên là cự li từ 3,5 m đến dưới 4 m; lập bảng tần số và tần số tương đối ghép nhóm.
Đề bài
Bạn Giang ghi lại cự li nhảy xa của các bạn trong câu lạc bộ thể thao ở bảng sau (đơn vị: mét)
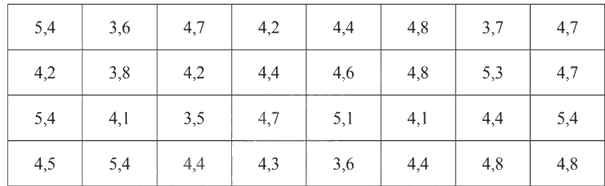
a) Để thu gọn bảng dữ liệu thì nên chọn bảng tần số không ghép nhóm hay bảng tần số ghép nhóm để biểu thị dữ liệu trên? Tại sao?
b) Hãy chia số liệu thành 4 nhóm, trong đó nhóm đầu tiên là cự li từ 3,5 m đến dưới 4 m; lập bảng tần số và tần số tương đối ghép nhóm.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Dựa vào: Bảng tần số ghép nhóm biểu diễn tần số của các nhóm số liệu. Bảng gồm hai dòng (hoặc hai cột), dòng (hoặc cột) thứ nhất ghi nhóm số liệu, dòng (hoặc cột) thứ hai ghi các tần số tương ứng với mỗi nhóm đó để giải thích.
- Lập bảng tần số tương đối ghép nhóm: Bảng tần số ghép nhóm biểu diễn tần số của các nhóm số liệu. Bảng gồm hai dòng (hoặc hai cột), dòng (hoặc cột) thứ nhất ghi nhóm số liệu, dòng (hoặc cột) thứ hai ghi các tần số tương ứng với mỗi nhóm đó. Tần số tương đối của một nhóm được tính theo công thức \(f = \frac{m}{N}.100\% \) trong đó m là tần số của nhóm và N là cỡ mẫu.
Lời giải chi tiết
a) Để thu gọn bảng dữ liệu thì nên chọn bảng tần số ghép nhóm để biểu thị dữ liệu trên vì bảng tần số ghép nhóm thể hiện nhóm biểu diễn tần số của các nhóm số liệu sẽ gọi hơn so với bảng tần số không ghép nhóm.
b) Chia số liệu thành 4 nhóm là: [3,5; 4), [4; 4,5), [4,5; 5), [5; 5,5)
Bảng tần số và tần số tương đối ghép nhóm:
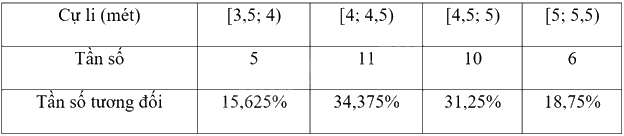
Bài tập 1 trang 46 SGK Toán 9 tập 2 - Chân trời sáng tạo thuộc chương trình học Toán 9, tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, giúp học sinh hiểu rõ hơn về ứng dụng của hàm số bậc nhất trong đời sống.
Bài tập 1 bao gồm các câu hỏi liên quan đến việc xác định hệ số góc và tung độ gốc của hàm số bậc nhất, vẽ đồ thị hàm số, và tìm tọa độ giao điểm của hai đường thẳng.
Để xác định hệ số góc và tung độ gốc của hàm số y = 2x - 3, ta so sánh với dạng tổng quát của hàm số bậc nhất y = ax + b. Trong đó:
Vậy, trong hàm số y = 2x - 3, ta có:
Để vẽ đồ thị hàm số y = 2x - 3, ta thực hiện các bước sau:
Để tìm tọa độ giao điểm của hai đường thẳng y = 2x - 3 và y = -x + 6, ta giải hệ phương trình sau:
| y = 2x - 3 | y = -x + 6 | |
|---|---|---|
| Phương trình 1 | y = 2x - 3 | |
| Phương trình 2 | y = -x + 6 |
Thay y = 2x - 3 vào phương trình y = -x + 6, ta được:
2x - 3 = -x + 6
3x = 9
x = 3
Thay x = 3 vào phương trình y = 2x - 3, ta được:
y = 2(3) - 3 = 3
Vậy, tọa độ giao điểm của hai đường thẳng y = 2x - 3 và y = -x + 6 là (3; 3).
Bài tập 1 trang 46 SGK Toán 9 tập 2 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số bậc nhất. Hy vọng với hướng dẫn chi tiết này, bạn đã có thể giải bài tập một cách dễ dàng và hiệu quả. Chúc bạn học tốt!