Bài tập 4 trang 82 SGK Toán 9 tập 1 thuộc chương trình Toán 9 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải phương trình bậc hai. Bài tập này thường yêu cầu học sinh áp dụng các công thức và phương pháp đã học để tìm ra nghiệm của phương trình.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 4 trang 82 SGK Toán 9 tập 1, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Cho tứ giác ABCD có (widehat B = widehat D = {90^o}). a) Chứng minh bốn điểm A, B, C, D cùng nằm trên một đường tròn. b) So sánh độ dài của AC và BD.
Đề bài
Cho tứ giác ABCD có \(\widehat B = \widehat D = {90^o}\).
a) Chứng minh bốn điểm A, B, C, D cùng nằm trên một đường tròn.
b) So sánh độ dài của AC và BD.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) - Sử dụng tính chất đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền.
- Chứng mình A, B, C, D cách đều 1 điểm nên nằm trên 1 đường tròn.
b) Dựa vào quan hệ giữa đường kính và dây cung.
Lời giải chi tiết
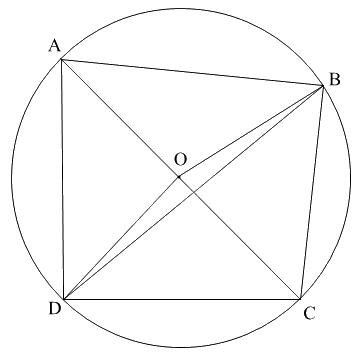
a) Gọi O là trung điểm của AC.
Xét tam giác ABC vuông tại B có O là trung điểm của AC nên \(OA = OB = OC = \frac{1}{2} AC\)
Xét tam giác ADC vuông tại D có O là trung điểm của AC nên \(OA = OD = OC = \frac{1}{2} AC\)
Suy ra \(OA = OB = OC = OD = \frac{1}{2} AC\) nên A, B, C, D cùng nằm trên một đường tròn tâm O đường kính AC.
b) Xét đường tròn tâm O đường kính AC có BD là dây cung không đi qua tâm O nên AC > BD.
Bài tập 4 trang 82 SGK Toán 9 tập 1 - Chân trời sáng tạo yêu cầu giải các phương trình bậc hai. Để giải quyết bài tập này, chúng ta cần nắm vững các kiến thức về phương trình bậc hai, bao gồm:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ đi vào giải chi tiết từng phương trình:
Ta có a = 1, b = -5, c = 6. Tính delta:
Δ = b2 - 4ac = (-5)2 - 4 * 1 * 6 = 25 - 24 = 1
Vì Δ > 0, phương trình có hai nghiệm phân biệt:
x1 = (-(-5) + √1) / (2 * 1) = (5 + 1) / 2 = 3
x2 = (-(-5) - √1) / (2 * 1) = (5 - 1) / 2 = 2
Vậy nghiệm của phương trình là x1 = 3 và x2 = 2.
Ta có a = 2, b = 7, c = 3. Tính delta:
Δ = b2 - 4ac = 72 - 4 * 2 * 3 = 49 - 24 = 25
Vì Δ > 0, phương trình có hai nghiệm phân biệt:
x1 = (-7 + √25) / (2 * 2) = (-7 + 5) / 4 = -1/2
x2 = (-7 - √25) / (2 * 2) = (-7 - 5) / 4 = -3
Vậy nghiệm của phương trình là x1 = -1/2 và x2 = -3.
Ta có a = 1, b = -4, c = 4. Tính delta:
Δ = b2 - 4ac = (-4)2 - 4 * 1 * 4 = 16 - 16 = 0
Vì Δ = 0, phương trình có nghiệm kép:
x = -b / (2a) = -(-4) / (2 * 1) = 2
Vậy nghiệm của phương trình là x = 2.
Khi giải phương trình bậc hai, các em cần lưu ý một số điều sau:
Phương trình bậc hai có rất nhiều ứng dụng trong thực tế, ví dụ như:
Hy vọng với lời giải chi tiết này, các em học sinh sẽ hiểu rõ hơn về cách giải bài tập 4 trang 82 SGK Toán 9 tập 1 - Chân trời sáng tạo và tự tin hơn trong việc học Toán 9.