Chào mừng bạn đến với bài học về Lý thuyết Không gian mẫu và biến cố trong chương trình Toán 9 Chân trời sáng tạo. Đây là một phần kiến thức quan trọng, đặt nền móng cho việc học về xác suất thống kê ở các lớp trên.
Bài học này sẽ cung cấp cho bạn những khái niệm cơ bản, công thức và ví dụ minh họa để bạn hiểu rõ về không gian mẫu, biến cố và cách tính xác suất của biến cố.
Phép thử ngẫu nhiên Các hoạt động mà ta không thể biết trước được kết quả của nó, nhưng biết tất cả các kết quả có thể xảy ra được gọi là phép thử ngẫu nhiên (còn gọi là phép thử).
Phép thử ngẫu nhiên
Các hoạt động mà ta không thể biết trước được kết quả của nó, nhưng biết tất cả các kết quả có thể xảy ra được gọi là phép thử ngẫu nhiên(còn gọi là phép thử). |
Không gian mẫu
Không gian mẫu, kí hiệu \(\Omega \), là tập hợp tất cả các kết quả có thể xảy ra của phép thử. |
Ví dụ: Bạn Lan gieo một con xúc xắc và bạn Hòa gieo một đồng xu được gọi là phép thử.
Kết quả của phép thử là số chấm xuất hiện trên con xúc xác và mặt xuất hiện của đồng xu.
Các kết quả có thể của phép thử là:
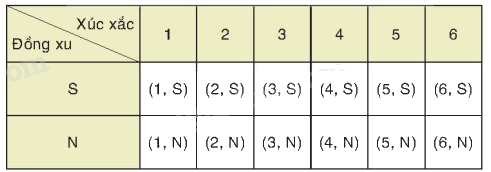
Mỗi ô là một kết quả có thể. Không gian mẫu là tập hợp 12 ô của bảng trên.
Do đó không gian mẫu của phép thử là:
\(\Omega = {\rm{\{ (1,S);(2,S);(3,S);(4,S);(5,S);(6,S);(1,N);(2,N);(3,N);(4,N);(5,N);(6,N)\} }}{\rm{.}}\)
Vậy không gian mẫu có 12 phần tử.
Chú ý: Khi biểu diễn các kết quả của phép thử, ta thường sử dụng:
- Dấu ngoặc tròn (…) để viết kết quả của phép thử lấy lần lượt từng vật.
- Dấu ngoặc nhọn {…} để viết kết quả của phép thử lấy đồng thời các vật.
Trong chương trình Toán 9, phần Lý thuyết Không gian mẫu và biến cố đóng vai trò quan trọng trong việc giới thiệu về môn Xác suất thống kê. Nắm vững kiến thức này sẽ giúp học sinh hiểu rõ hơn về các khái niệm cơ bản và ứng dụng của xác suất trong thực tế.
Định nghĩa: Không gian mẫu (Ω) là tập hợp tất cả các kết quả có thể xảy ra của một thí nghiệm hoặc một sự kiện.
Ví dụ:
Định nghĩa: Biến cố (A) là một tập con của không gian mẫu Ω. Nói cách khác, biến cố là một tập hợp các kết quả thỏa mãn một điều kiện nào đó.
Ví dụ:
Có một số loại biến cố thường gặp:
Có một số phép toán cơ bản trên các biến cố:
Định nghĩa: Xác suất của biến cố A, ký hiệu P(A), là tỷ lệ giữa số các kết quả thuận lợi cho A và tổng số các kết quả có thể xảy ra.
Công thức: P(A) = n(A) / n(Ω), trong đó n(A) là số phần tử của biến cố A và n(Ω) là số phần tử của không gian mẫu Ω.
Bài toán: Gieo một xúc xắc 6 mặt. Tính xác suất để xuất hiện mặt 5.
Giải:
Hãy tự giải các bài tập sau để củng cố kiến thức:
Hy vọng bài học này đã giúp bạn hiểu rõ hơn về Lý thuyết Không gian mẫu và biến cố Toán 9 Chân trời sáng tạo. Chúc bạn học tốt!