Chào mừng bạn đến với bài học về Tỉ số lượng giác của góc nhọn trong chương trình Toán 9 Chân trời sáng tạo. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về các tỉ số lượng giác, giúp bạn giải quyết các bài toán liên quan một cách hiệu quả.
Chúng ta sẽ cùng nhau tìm hiểu định nghĩa, các hệ thức lượng trong tam giác vuông, và ứng dụng của tỉ số lượng giác trong việc giải tam giác vuông.
1. Định nghĩa tỉ số lượng giác của một góc nhọn \({\rm{sin\alpha }} = \frac{{cạnh\,đối}}{{cạnh\,huyền}};{\rm{cos\alpha }} = \frac{{cạnh\,kề}}{{cạnh\,huyền}};\) \({\rm{tan\alpha }} = \frac{{cạnh\,đối}}{{cạnh\,kề}};{\rm{cot\alpha }} = \frac{{cạnh\,kề}}{{cạnh\,đối}}.\) \(\cot \alpha = \frac{1}{{\tan \alpha }}\). \(\sin \alpha ,\cos \alpha ,\tan \alpha ,\cot \alpha \) gọi là các tỉ số lượng giác của góc nhọn \(\alpha \).
1. Định nghĩa tỉ số lượng giác của một góc nhọn
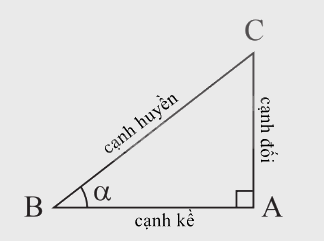
\({\rm{sin\alpha }} = \frac{{cạnh\,đối}}{{cạnh\,huyền}};{\rm{cos\alpha }} = \frac{{cạnh\,kề}}{{cạnh\,huyền}};\) \({\rm{tan\alpha }} = \frac{{cạnh\,đối}}{{cạnh\,kề}};{\rm{cot\alpha }} = \frac{{cạnh\,kề}}{{cạnh\,đối}}.\) \(\cot \alpha = \frac{1}{{\tan \alpha }}\).
|
Tip học thuộc nhanh:
Sin đi học Cos không hư Tan đoàn kết Cotan kết đoàn |
Chú ý: Với góc nhọn \(\alpha \), ta có:
\(0 < \sin \alpha < 1\); \(0 < \cos \alpha < 1\).
\(\cot \alpha = \frac{1}{{\tan \alpha }}\).
Ví dụ:
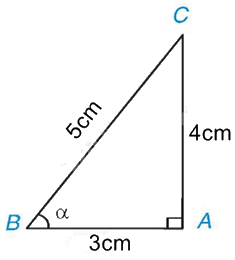
Theo định nghĩa của tỉ số lượng giác, ta có:
\(\sin \alpha = \frac{{AC}}{{BC}} = \frac{4}{5}\), \(\cos \alpha = \frac{{AB}}{{BC}} = \frac{3}{5}\), \(\tan \alpha = \frac{{AC}}{{AB}} = \frac{4}{3}\), \(\cot \alpha = \frac{{AB}}{{AC}} = \frac{3}{4}\)
Bảng giá trị lượng giác của các góc nhọn đặc biệt
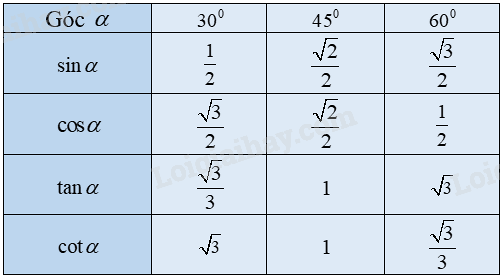
Ví dụ: \(P = \frac{{\sin {{30}^0}.\cos {{60}^0}}}{{\tan {{45}^0}}} = \frac{{\frac{1}{2}.\frac{1}{2}}}{1} = \frac{1}{4}\).
2. Tỉ số lượng giác của hai góc phụ nhau
Định lí về tỉ số lượng giác của hai góc phụ nhau
Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tan góc này bằng côtang góc kia. \(\begin{array}{*{20}{c}}{\sin \left( {{{90}^0} - \alpha } \right) = \cos \alpha ;}&{\cos \left( {{{90}^0} - \alpha } \right) = \sin \alpha ;}\\{\tan \left( {{{90}^0} - \alpha } \right) = \cot \alpha ;}&{\cot \left( {{{90}^0} - \alpha } \right) = \tan \alpha .}\end{array}\) |
Ví dụ:
\(\begin{array}{l}\sin {60^0} = \cos \left( {{{90}^0} - {{60}^0}} \right) = \cos {30^0};\\\cos {52^0}30' = \sin \left( {{{90}^0} - {{52}^0}30'} \right) = \sin {37^0}30';\\\tan {80^0} = \cot \left( {{{90}^0} - {{80}^0}} \right) = \cot {10^0};\\\cot {82^0} = \tan \left( {{{90}^0} - {{82}^0}} \right) = \tan {8^0}.\end{array}\)
3. Sử dụng máy tính cầm tay tính tỉ số lượng giác của một góc nhọn
Người ta thường dùng các đơn vị số đo góc là độ (kí hiệu: \(^0\)), phút (kí hiệu: \('\)), giây (kí hiệu: \(''\)).
Ta có thể sử dụng nhiều loại máy tính cầm tay để tính các tỉ số lượng giác của góc nhọn và tính số đo của góc nhọn khi biết một tỉ số lượng giác của nó.
Lưu ý: ta cần đổi đơn vị đo về độ.

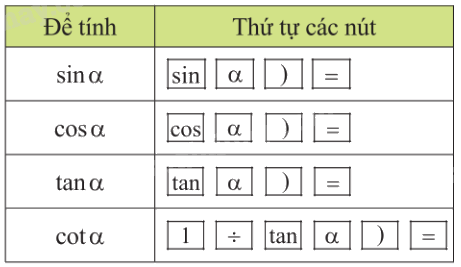
Tính các tỉ số lượng giác của các góc nhọn
Để tính tỉ số lượng giác của một góc \(\alpha \), ta dùng các nút:

Để tính \(\cot \alpha \), ta tính \(\cot \alpha = \frac{1}{{\tan \alpha }}\) hoặc \(\tan \left( {{{90}^0} - \alpha } \right)\).
Bảng tóm tắt cách tính tỉ số lượng giác của một góc nhọn
Xác định số đo của góc nhọn khi biết một tỉ số lượng giác của góc đó
Bảng tóm tắt cách tính số đo của một góc nhọn khi biết một tỉ số lượng giác
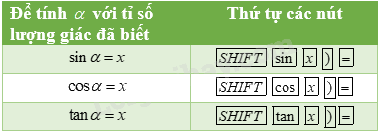
Để tìm \(\alpha \) khi biết \(\cot \alpha \), ta tính \(\tan \alpha = \frac{1}{{\cot \alpha }}\) và dùng \(\tan \alpha \) để tính \(\alpha \).
Một số công thức mở rộng:
+) \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\)
+) \(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}\)
+) \(\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }}\)
+) \(\tan \alpha .\cot \alpha = 1\)
+) \(\frac{1}{{{{\cos }^2}\alpha }} = {\tan ^2}\alpha + 1\)
+) \(\frac{1}{{{{\sin }^2}\alpha }} = {\cot ^2}\alpha + 1\)
Trong chương trình Toán 9, phần Tỉ số lượng giác của góc nhọn đóng vai trò quan trọng, là nền tảng cho việc giải quyết nhiều bài toán hình học và ứng dụng thực tế. Bài viết này sẽ trình bày chi tiết lý thuyết, ví dụ minh họa và bài tập thực hành để giúp học sinh nắm vững kiến thức này.
Xét tam giác vuông ABC vuông tại A. Gọi AB = c, AC = b, BC = a. Khi đó:
Tương tự, ta có thể định nghĩa sin, cos, tan, cot của góc C.
Các hệ thức lượng trong tam giác vuông liên quan đến tỉ số lượng giác và các cạnh của tam giác:
Ngoài ra, ta còn có định lý Pytago: a2 = b2 + c2
Dưới đây là bảng giá trị lượng giác của một số góc đặc biệt thường gặp:
| Góc | 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|---|
| sin | 0 | 1/2 | √2/2 | √3/2 | 1 |
| cos | 1 | √3/2 | √2/2 | 1/2 | 0 |
| tan | 0 | 1/√3 | 1 | √3 | Không xác định |
| cot | Không xác định | √3 | 1 | 1/√3 | 0 |
Nếu hai góc A và B bù nhau (A + B = 90°), thì:
Tỉ số lượng giác được sử dụng để giải tam giác vuông, tức là tìm các cạnh và góc còn lại khi biết một số cạnh và góc. Ví dụ:
Cho tam giác ABC vuông tại A, biết AB = 5cm và góc B = 30°. Tính AC và BC.
Giải:
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về Tỉ số lượng giác của góc nhọn Toán 9 Chân trời sáng tạo. Chúc bạn học tập tốt!