Chào mừng bạn đến với bài học về lý thuyết Góc ở tâm và góc nội tiếp trong chương trình Toán 9 Chân trời sáng tạo. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về hai loại góc này, cùng với các định lý liên quan.
Chúng ta sẽ cùng nhau khám phá định nghĩa, tính chất, và cách áp dụng lý thuyết vào giải các bài tập thực tế. Mục tiêu là giúp bạn hiểu sâu sắc và tự tin khi làm bài kiểm tra.
1. Góc ở tâm Định nghĩa Góc ở tâm là góc có đỉnh trùng với tâm đường tròn.
1. Góc ở tâm
Định nghĩa
Góc ở tâm là góc có đỉnh trùng với tâm đường tròn. |
2. Cung, số đo cung
Cung
Mỗi phần đường tròn giới hạn bởi hai điểm A, B trên đường tròn gọi là một cung AB, kí hiệu là $\overset\frown{AB}$. |
Ví dụ:
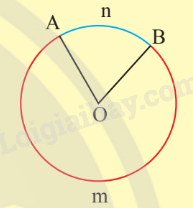
Góc ở tâm \(\widehat {AOB}\) chắn cung AnB hay cung AnB bị chắn bởi góc ở tâm \(\widehat {AOB}\).
$\overset\frown{AnB}$ là cung nhỏ và $\overset\frown{AmB}$ là cung lớn.
Số đo cung
- Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó. - Số đo của cung lớn bằng: \({360^0}\) - số đo cung nhỏ có chung đầu mút với cung lớn. - Số đo của cung nửa đường tròn bằng \({180^0}\). - Số đo của cung AB được kí hiệu là sđ$\overset\frown{AB}$. |
Chú ý:
- Cung nhỏ có số đo nhỏ hơn \({180^0}\), cung lớn có số đo lớn hơn \({180^0}\). Cung nửa đường tròn có số đo \({180^0}\).
- Khi hai mút của cung trùng nhau, ta có cung không với số đo \({0^0}\) và cung cả đường tròn có số đo \({360^0}\).
- Một cung có số đo \({n^0}\) thường được gọi tắt là cung \({n^0}\).
- Trong một đường tròn, hai cung được gọi là bằng nhau nếu chúng có số đo bằng nhau.
3. Góc nội tiếp
Định nghĩa
Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó. Cung nằm bên trong của góc được gọi là cung bị chắn. |
Số đo góc nội tiếp
Trong một đường tròn, số đo của góc nội tiếp bằng nửa số đo của cung bị chắn. |
Ví dụ:
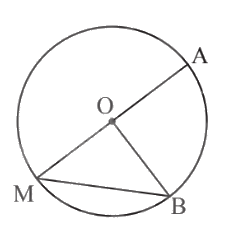
\(\widehat {AMB}\)là góc nội tiếp chắn $\overset\frown{AB}$ trên đường tròn (O) nên \(\widehat {AMB} = \frac{1}{2}\)sđ$\overset\frown{AB}$.
Chú ý: Trong một đường tròn:
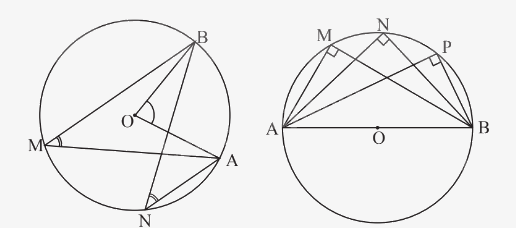
- Các góc nội tiếp bằng nhau chắn các cung bằng nhau.
- Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
- Góc nội tiếp nhỏ hơn hoặc bằng \({90^o}\) có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.
Góc nội tiếp chắn nửa đường tròn là góc vuông.
Trong chương trình Toán 9, kiến thức về đường tròn đóng vai trò quan trọng, và góc ở tâm, góc nội tiếp là những khái niệm then chốt. Việc nắm vững lý thuyết và kỹ năng giải bài tập liên quan sẽ giúp học sinh đạt kết quả tốt trong các kỳ thi.
Định nghĩa: Góc ở tâm là góc có đỉnh là tâm đường tròn và hai cạnh chứa hai bán kính.
Số đo: Số đo của góc ở tâm bằng số đo của cung bị chắn.
Ví dụ: Nếu cung AB có số đo 60 độ thì góc AOB (với O là tâm đường tròn) cũng có số đo 60 độ.
Định nghĩa: Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung.
Số đo: Số đo của góc nội tiếp bằng nửa số đo của cung bị chắn.
Ví dụ: Nếu cung AC có số đo 80 độ thì góc ABC (với B nằm trên đường tròn) có số đo 40 độ.
Góc ở tâm cùng chắn một cung thì có số đo bằng hai lần số đo của góc nội tiếp cùng chắn cung đó.
Công thức: ∠AOB = 2∠ACB (với O là tâm đường tròn, A, B, C là các điểm trên đường tròn)
Bài 1: Cho đường tròn (O) và góc nội tiếp ∠ABC = 50 độ. Tính số đo cung AC.
Giải: Số đo cung AC = 2 * ∠ABC = 2 * 50 độ = 100 độ.
Bài 2: Cho đường tròn (O) và góc ở tâm ∠AOB = 80 độ. Tính số đo góc nội tiếp ∠ACB chắn cung AB.
Giải: ∠ACB = ∠AOB / 2 = 80 độ / 2 = 40 độ.
Lý thuyết về góc ở tâm và góc nội tiếp được ứng dụng rộng rãi trong việc giải các bài tập liên quan đến đường tròn, đặc biệt là các bài toán chứng minh hệ thức, tính góc, tính độ dài cung và dây cung.
Để nắm vững lý thuyết, bạn nên luyện tập thường xuyên với các bài tập khác nhau. Hãy bắt đầu với những bài tập cơ bản, sau đó dần dần nâng cao độ khó. Đừng ngại hỏi thầy cô hoặc bạn bè nếu gặp khó khăn.
Bài học về lý thuyết Góc ở tâm, góc nội tiếp Toán 9 Chân trời sáng tạo đã cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất. Hãy ghi nhớ các định nghĩa, tính chất, và định lý liên quan để áp dụng vào giải bài tập một cách hiệu quả. Chúc bạn học tốt!