Giaitoan.edu.vn xin giới thiệu lời giải chi tiết mục 1 trang 39 SGK Toán 9 tập 2 - Chân trời sáng tạo. Bài giải được trình bày rõ ràng, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các bài giải Toán 9 tập 2, đáp ứng nhu cầu học tập của học sinh trên toàn quốc.
Bác Mai cân các quả dưa trong cửa hàng và ghi lại cân nặng (đơn vị: kg) của từng quả như sau: Để thuận tiện cho việc kinh doanh, bác Mai chia dưa thành 4 nhóm theo cân nặng (kí hiệu là X): (4 le X < 4,5;4,5 le X < 5;5 le X < 5,5;5,5 le X < 6.) Hãy hoàn thành bảng số liệu sau:
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 1 trang 39 SGK Toán 9 Chân trời sáng tạo
Bảng sau ghi lại một thời gian của bác sĩ khám cho một số bệnh nhân (đơn vị: phút):

a) Hãy chia số liệu thành 5 nhóm, với nhóm thứ nhất là các bệnh nhân có thời gian khám từ 5 phút đến dưới 6,5 phút và lập bảng tần số ghép nhóm.
b) Xác định nhóm có tần số cao nhất và nhóm có tần số thấp nhất.
Phương pháp giải:
- Dựa vào: Số lượng các giá trị của mẫu số liệu thuộc vào một nhóm được gọi là tần số của nhóm.
- Bảng tần số ghép nhóm biểu diễn tần số của các nhóm số liệu. Bảng gồm hai dòng (hoặc hai cột), dòng (hoặc cột) thứ nhất ghi nhóm số liệu, dòng (hoặc cột) thứ hai ghi các tần số tương ứng với mỗi nhóm đó.
- Nhìn vào bảng tần số ghép nhóm nhận xét.
Lời giải chi tiết:
a) Chia số liệu thành 5 nhóm theo số phút (kí hiệu X):
[5; 6,5) , [6,5; 8) , [8; 9,5) , [9,5; 11) , [11; 12,5).
Bảng tần số ghép nhóm của mẫu số liệu:

b) Nhóm có tần số cao nhất là [5; 6,5) , [6,5; 8)
Nhóm có tần số thấp nhất là [9,5; 11).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 1 trang 39 SGK Toán 9 Chân trời sáng tạo
Bác Mai cân các quả dưa trong cửa hàng và ghi lại cân nặng (đơn vị: kg) của từng quả như sau:
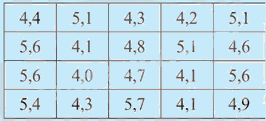
Để thuận tiện cho việc kinh doanh, bác Mai chia dưa thành 4 nhóm theo cân nặng (kí hiệu là X):
\(4 \le X < 4,5;4,5 \le X < 5;5 \le X < 5,5;5,5 \le X < 6.\)
Hãy hoàn thành bảng số liệu sau:
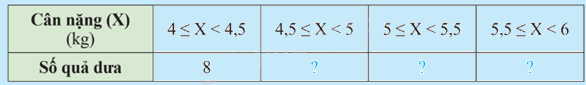
Phương pháp giải:
Xét từng giá trị nằm trong các khoảng.
Lời giải chi tiết:
Ta được bảng số liệu sau:
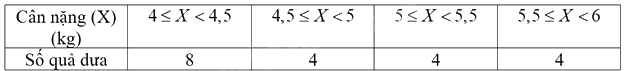
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 1 trang 39 SGK Toán 9 Chân trời sáng tạo
Bác Mai cân các quả dưa trong cửa hàng và ghi lại cân nặng (đơn vị: kg) của từng quả như sau:
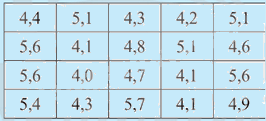
Để thuận tiện cho việc kinh doanh, bác Mai chia dưa thành 4 nhóm theo cân nặng (kí hiệu là X):
\(4 \le X < 4,5;4,5 \le X < 5;5 \le X < 5,5;5,5 \le X < 6.\)
Hãy hoàn thành bảng số liệu sau:
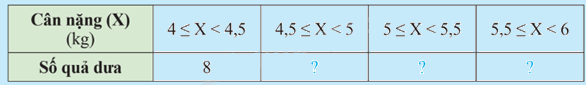
Phương pháp giải:
Xét từng giá trị nằm trong các khoảng.
Lời giải chi tiết:
Ta được bảng số liệu sau:
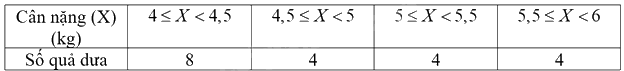
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 1 trang 39 SGK Toán 9 Chân trời sáng tạo
Bảng sau ghi lại một thời gian của bác sĩ khám cho một số bệnh nhân (đơn vị: phút):

a) Hãy chia số liệu thành 5 nhóm, với nhóm thứ nhất là các bệnh nhân có thời gian khám từ 5 phút đến dưới 6,5 phút và lập bảng tần số ghép nhóm.
b) Xác định nhóm có tần số cao nhất và nhóm có tần số thấp nhất.
Phương pháp giải:
- Dựa vào: Số lượng các giá trị của mẫu số liệu thuộc vào một nhóm được gọi là tần số của nhóm.
- Bảng tần số ghép nhóm biểu diễn tần số của các nhóm số liệu. Bảng gồm hai dòng (hoặc hai cột), dòng (hoặc cột) thứ nhất ghi nhóm số liệu, dòng (hoặc cột) thứ hai ghi các tần số tương ứng với mỗi nhóm đó.
- Nhìn vào bảng tần số ghép nhóm nhận xét.
Lời giải chi tiết:
a) Chia số liệu thành 5 nhóm theo số phút (kí hiệu X):
[5; 6,5) , [6,5; 8) , [8; 9,5) , [9,5; 11) , [11; 12,5).
Bảng tần số ghép nhóm của mẫu số liệu:

b) Nhóm có tần số cao nhất là [5; 6,5) , [6,5; 8)
Nhóm có tần số thấp nhất là [9,5; 11).
Mục 1 trang 39 SGK Toán 9 tập 2 - Chân trời sáng tạo thường xoay quanh các bài toán liên quan đến hàm số bậc nhất, bao gồm việc xác định hệ số góc, phương trình đường thẳng, và ứng dụng của hàm số trong các bài toán thực tế. Việc nắm vững kiến thức về hàm số bậc nhất là nền tảng quan trọng cho các chương trình học toán ở các lớp trên.
Mục 1 thường tập trung vào việc củng cố các khái niệm cơ bản về hàm số bậc nhất, bao gồm:
Để giải các bài toán trong Mục 1 trang 39 SGK Toán 9 tập 2 - Chân trời sáng tạo, học sinh cần nắm vững các phương pháp sau:
Bài toán: Tìm phương trình đường thẳng đi qua điểm A(1; 2) và có hệ số góc là 3.
Giải:
Phương trình đường thẳng có dạng y = ax + b. Vì hệ số góc a = 3, phương trình trở thành y = 3x + b.
Thay tọa độ điểm A(1; 2) vào phương trình, ta có: 2 = 3(1) + b => b = -1.
Vậy phương trình đường thẳng cần tìm là y = 3x - 1.
Để nắm vững kiến thức về hàm số bậc nhất và rèn luyện kỹ năng giải toán, học sinh nên:
Ngoài các kiến thức cơ bản về hàm số bậc nhất, học sinh có thể tìm hiểu thêm về:
Giaitoan.edu.vn hy vọng rằng với lời giải chi tiết và phương pháp giải rõ ràng này, các em học sinh sẽ tự tin hơn trong việc học tập và giải các bài toán Toán 9 tập 2 - Chân trời sáng tạo. Chúc các em học tốt!