Chào mừng bạn đến với bài học về lý thuyết Tứ giác nội tiếp trong chương trình Toán 9 Chân trời sáng tạo. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về tứ giác nội tiếp, giúp bạn giải quyết các bài toán liên quan một cách hiệu quả.
Chúng ta sẽ cùng nhau tìm hiểu định nghĩa, tính chất, dấu hiệu nhận biết tứ giác nội tiếp và các ứng dụng thực tế của nó trong hình học.
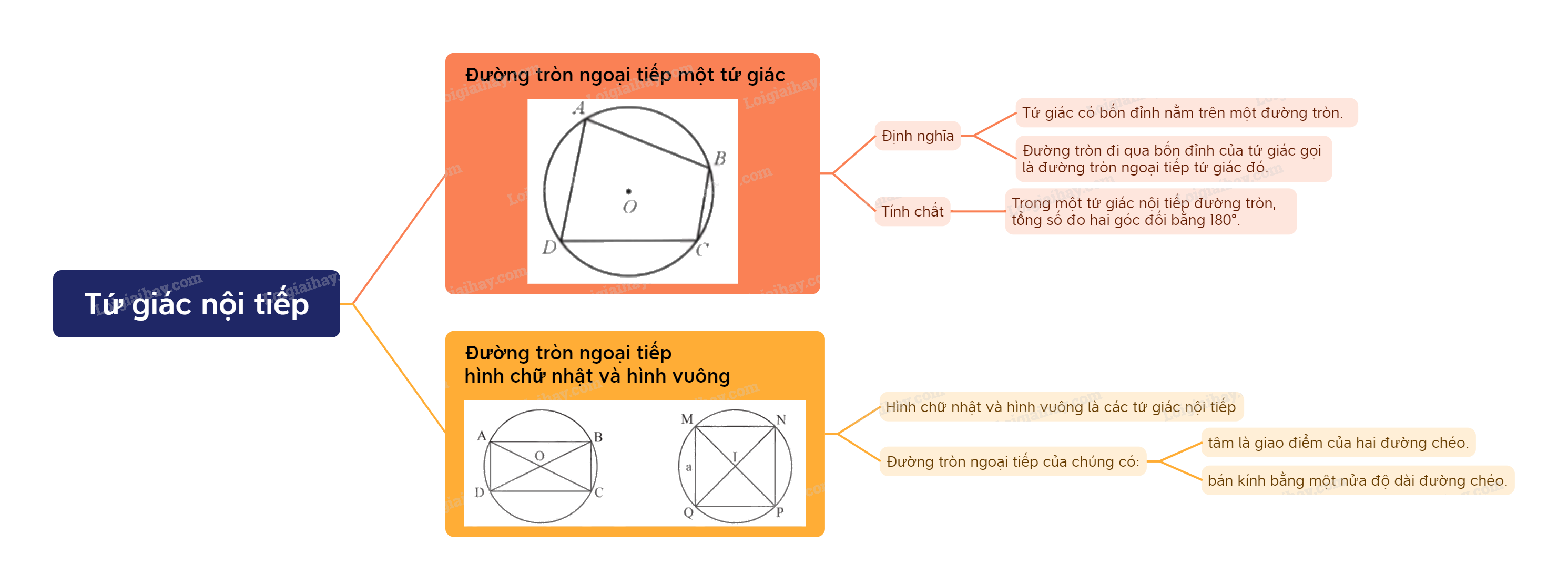
1. Đường tròn ngoại tiếp của một tứ giác Định nghĩa đường tròn ngoại tiếp tứ giác - Một tứ giác có bốn đỉnh nằm trên một đường tròn được gọi là tứ giác nội tiếp đường tròn (gọi tắt là tứ giác nội tiếp). - Đường tròn đi qua bốn đỉnh của tứ giác gọi là đường tròn ngoại tiếp tứ giác đó.
1. Đường tròn ngoại tiếp của một tứ giác
Định nghĩa đường tròn ngoại tiếp tứ giác
- Một tứ giác có bốn đỉnh nằm trên một đường tròn được gọi là tứ giác nội tiếp đường tròn (gọi tắt là tứ giác nội tiếp). - Đường tròn đi qua bốn đỉnh của tứ giác gọi là đường tròn ngoại tiếp tứ giác đó. |
Ví dụ:
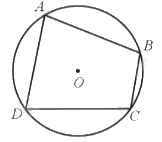
Tứ giác ABCD là tứ giác nội tiếp và đường tròn (O) được gọi là đường tròn ngoại tiếp tứ giác ABCD.
Tính chất
Trong một tứ giác nội tiếp đường tròn, tổng số đo hai góc đối bằng \(180^\circ \). |
Ví dụ:
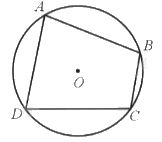
Tứ giác ABCD nội tiếp (O) nên \(\widehat A + \widehat C = 180^\circ ;\widehat B + \widehat D = 180^\circ \).
2. Đường tròn ngoại tiếp hình chữ nhật và hình vuông
- Hình chữ nhật, hình vuông là các tứ giác nội tiếp. - Đường tròn ngoại tiếp hình chữ nhật, hình vuông có tâm là giao điểm của hai đường chéo và có bán kính bằng nửa đường chéo.
|
Ví dụ:
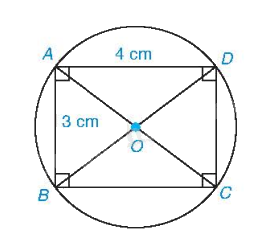
Áp dụng định lí Pythagore cho tam giác ABD vuông tại A, ta có:
\(B{D^2} = A{B^2} + A{D^2} = {3^2} + {4^2} = 25\) nên \(BD = 5cm\).
Do đó, ta có \(R = \frac{{BD}}{2} = 2,5cm\).
Đường tròn (O;2,5) là đường tròn ngoại tiếp hình chữ nhật ABCD.
Tứ giác nội tiếp là một khái niệm quan trọng trong chương trình Hình học lớp 9, đặc biệt là trong sách giáo khoa Toán 9 Chân trời sáng tạo. Hiểu rõ lý thuyết này là nền tảng để giải quyết nhiều bài toán phức tạp và nâng cao kiến thức về hình học.
Một tứ giác được gọi là tứ giác nội tiếp đường tròn nếu bốn đỉnh của nó cùng nằm trên một đường tròn. Nói cách khác, tồn tại một đường tròn đi qua cả bốn đỉnh của tứ giác đó.
Có một số dấu hiệu để nhận biết một tứ giác là tứ giác nội tiếp:
Lý thuyết tứ giác nội tiếp có nhiều ứng dụng trong việc giải các bài toán hình học, đặc biệt là các bài toán liên quan đến đường tròn và các góc trong hình tròn.
Ví dụ, chúng ta có thể sử dụng tính chất tổng hai góc đối nhau bằng 180° để tính góc trong một tứ giác nội tiếp, hoặc để chứng minh một tứ giác là tứ giác nội tiếp.
Bài tập 1: Cho tứ giác ABCD nội tiếp đường tròn. Biết góc A = 80° và góc C = 100°. Tính số đo góc B và góc D.
Giải:
Vì ABCD là tứ giác nội tiếp, ta có:
Do đó, góc B = 180° - góc D và góc D = 180° - góc B.
Bài tập 2: Cho tam giác ABC vuông tại A. Vẽ đường tròn đường kính BC. Gọi D là một điểm trên đường tròn (D khác A, B, C). Chứng minh tứ giác ABDC là tứ giác nội tiếp.
Giải:
Vì tam giác ABC vuông tại A, nên góc BAC = 90°. Do đó, BC là đường kính của đường tròn ngoại tiếp tam giác ABC.
Vì D nằm trên đường tròn đường kính BC, nên góc BDC = 90° (góc nội tiếp chắn nửa đường tròn).
Xét tứ giác ABDC, ta có: góc BAC + góc BDC = 90° + 90° = 180°. Do đó, tứ giác ABDC là tứ giác nội tiếp.
Ngoài những kiến thức cơ bản trên, bạn có thể tìm hiểu thêm về các ứng dụng nâng cao của tứ giác nội tiếp trong các bài toán hình học phức tạp hơn. Ví dụ, việc sử dụng các định lý về đường tròn ngoại tiếp, đường tròn nội tiếp và các tính chất liên quan đến các đoạn thẳng và góc trong tứ giác nội tiếp.
Hy vọng bài học này đã giúp bạn hiểu rõ hơn về lý thuyết Tứ giác nội tiếp Toán 9 Chân trời sáng tạo. Chúc bạn học tập tốt!