Chào mừng bạn đến với bài học về lý thuyết bất phương trình bậc nhất một ẩn trong chương trình Toán 9 Chân trời sáng tạo. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về bất phương trình, giúp bạn tự tin giải quyết các bài toán liên quan.
Chúng ta sẽ cùng nhau tìm hiểu định nghĩa, các tính chất, quy tắc biến đổi bất phương trình và cách giải bất phương trình bậc nhất một ẩn một cách chi tiết và dễ hiểu.
1. Bất phương trình bậc nhất một ẩn, nghiệm của bất phương trình bậc nhất một ẩn Khái niệm bất phương trình bậc nhất một ẩn
1. Bất phương trình bậc nhất một ẩn, nghiệm của bất phương trình bậc nhất một ẩn
Khái niệm bất phương trình bậc nhất một ẩn
Bất phương trình dạng \(ax + b < 0\) (hoặc \(ax + b > 0\); \(ax + b \le 0\); \(ax + b \ge 0\)) trong đó a, b là hai số đã cho, \(a \ne 0\) được gọi là bất phương trình bậc nhất một ẩn (ẩn là x). |
Ví dụ: \(3x + 16 \le 0\); \( - 3x > 0\) là các bất phương trình bậc nhất một ẩn x.
\({x^2} - 4 \ge 0\) không phải là một bất phương trình bậc nhất một ẩn x vì \({x^2} - 4\) là một đa thức bậc hai.
\(3x - 2y < 2\) không phải là một bất phương trình bậc nhất một ẩn vì đa thức \(3x - 2y\) là đa thức với hai biến x và y.
Nghiệm của bất phương trình
Với bất phương trình bậc nhất có ẩn là x, số \({x_0}\) được gọi là một nghiệm của bất phương trình nếu ta thay \(x = {x_0}\) thì nhận được một khẳng định đúng. Giải bất phương trình là tìm tất cả các nghiệm của nó. |
Ví dụ:
\(x = - 2\) là nghiệm của bất phương trình \(2x - 10 < 0\) vì \(2.\left( { - 2} \right) - 10 = - 4 - 10 = - 14 < 0\).
\(x = 6\) không là nghiệm của bất phương trình \(2x - 10 < 0\) vì \(2.6 - 10 = 12 - 10 = 2 > 0\).
2. Giải bất phương trình bậc nhất một ẩn
Xét bất phương trình \(ax + b > 0\left( {a \ne 0} \right)\). - Cộng hai vế của bất phương trình với –b, ta được bất phương trình: \(ax > - b\). - Nhân hai vế của bất phương trình nhận được với \(\frac{1}{a}\): + Nếu \(a > 0\) thì nhận được nghiệm của bất phương trình đã cho là: \(x > - \frac{b}{a}\). + Nếu \(a < 0\) thì nhận được nghiệm của bất phương trình đã cho là: \(x < - \frac{b}{a}\). |
Chú ý: Với các bất phương trình \(ax + b < 0\), \(ax + b \le 0\), \(ax + b \ge 0\), ta thực hiện các bước giải tương tự.
Ví dụ:Giải bất phương trình \( - 2x - 4 > 0\)
Lời giải:Ta có:
\(\begin{array}{l} - 2x - 4 > 0\\ - 2x > 0 + 4\\ - 2x > 4\\x < 4.\left( { - \frac{1}{2}} \right)\\x < - 2\end{array}\)
Vậy nghiệm của bất phương trình là \(x < - 2\).
Chú ý: Bằng cách sử dụng các tính chất của bất đẳng thức, ta có thể giải một số bất phương trình đưa được về bất phương trình bậc nhất một ẩn \(ax + b < 0\), \(ax + b > 0\), \(ax + b \le 0\), \(ax + b \ge 0\).
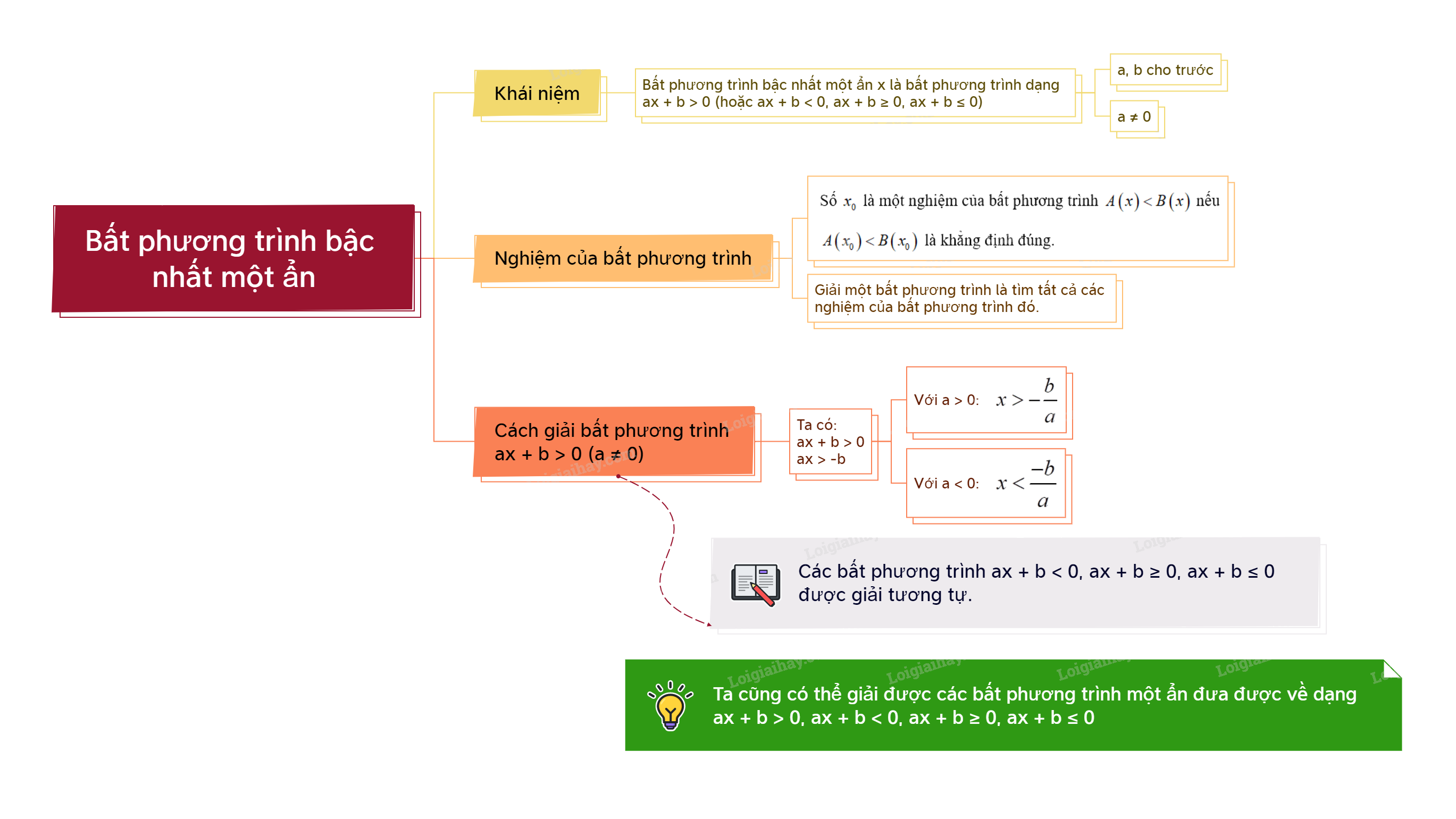
Bất phương trình bậc nhất một ẩn là một công cụ quan trọng trong toán học, được sử dụng để mô tả và giải quyết các bài toán thực tế liên quan đến sự so sánh và giới hạn. Trong chương trình Toán 9 Chân trời sáng tạo, việc nắm vững lý thuyết và kỹ năng giải bất phương trình bậc nhất một ẩn là điều kiện cần thiết để đạt kết quả tốt trong các kỳ thi và ứng dụng vào cuộc sống.
Bất phương trình bậc nhất một ẩn là bất phương trình có dạng:
Trong đó:
Các tính chất quan trọng của bất phương trình bao gồm:
Để giải bất phương trình, chúng ta sử dụng các quy tắc biến đổi sau:
Các bước giải bất phương trình bậc nhất một ẩn:
Ví dụ 1: Giải bất phương trình 2x + 3 < 7
Giải:
Vậy tập nghiệm của bất phương trình là x < 2.
Ví dụ 2: Giải bất phương trình -3x + 5 ≥ 1
Giải:
Vậy tập nghiệm của bất phương trình là x ≤ 4/3.
Để củng cố kiến thức, bạn hãy tự giải các bài tập sau:
Lý thuyết bất phương trình bậc nhất một ẩn là nền tảng quan trọng để giải quyết các bài toán phức tạp hơn trong toán học. Việc nắm vững các định nghĩa, tính chất, quy tắc biến đổi và kỹ năng giải bất phương trình sẽ giúp bạn tự tin hơn trong học tập và ứng dụng vào thực tế.