Chào mừng bạn đến với bài học về lý thuyết Tính chất của phép khai phương trong chương trình Toán 9 Chân trời sáng tạo. Bài học này sẽ cung cấp cho bạn những kiến thức cơ bản và quan trọng nhất về phép khai phương, giúp bạn giải quyết các bài toán một cách hiệu quả.
Chúng ta sẽ cùng nhau khám phá các tính chất của phép khai phương, cách áp dụng chúng vào giải toán và những lưu ý quan trọng để tránh sai lầm. Hãy bắt đầu ngay thôi!
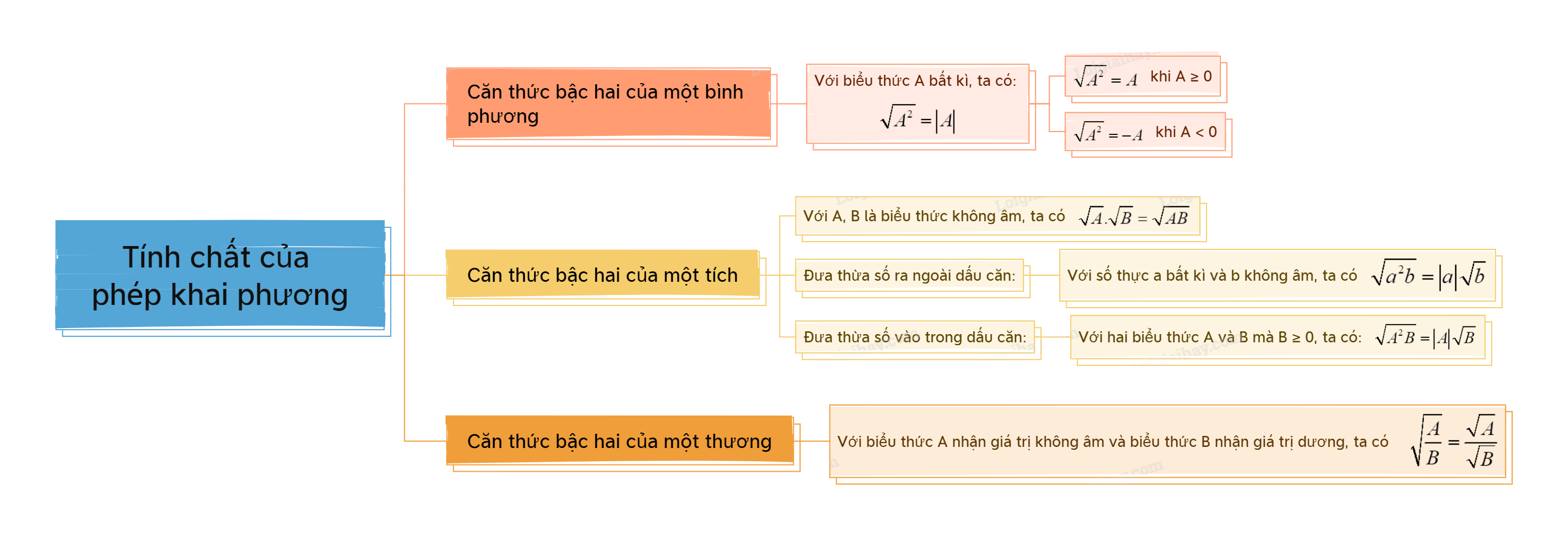
1. Căn thức bậc hai của một bình phương Tính chất Với biểu thức A bất kì, ta có (sqrt {{A^2}} = left| A right|), nghĩa là (sqrt {{A^2}} = A) khi (A ge 0); (sqrt {{A^2}} = - A) khi (A < 0).
1. Căn thức bậc hai của một bình phương
Tính chất
Với biểu thức A bất kì, ta có \(\sqrt {{A^2}} = \left| A \right|\), nghĩa là \(\sqrt {{A^2}} = A\) khi \(A \ge 0\); \(\sqrt {{A^2}} = - A\) khi \(A < 0\). |
Ví dụ: Với \(x < 0\), ta có 1 – x > 0. Do đó \({\left( {\sqrt {1 - x} } \right)^2} = 1 - x\).
2. Căn thức bậc hai của một tích
Với hai biểu thức A và B nhận giá trị không âm, ta có \(\sqrt A .\sqrt B = \sqrt {AB} \). |
Ví dụ:
\(\sqrt {27} .\sqrt 3 = \sqrt {27.3} = \sqrt {81} = 9\)
Với \(a \ge 0,b < 0\) thì \(\sqrt {25{a^2}{b^2}} = \sqrt {{5^2}.{a^2}.{{\left( { - b} \right)}^2}} = \sqrt {{5^2}} .\sqrt {{a^2}} .\sqrt {{{\left( { - b} \right)}^2}} = 5.a.\left( { - b} \right) = - 5ab\).
Nhận xét: Ta có thể biến đổi \(\sqrt {ab} = \sqrt a .\sqrt b \) hoặc \(\sqrt a .\sqrt b = \sqrt {ab} \) (\(a \ge 0\) và \(b \ge 0\)) để việc tính toán được dễ dàng hơn.
Với số thực a bất kì và b không âm, ta có \(\sqrt {{a^2}b} = \left| a \right|\sqrt b \). Biến đổi này được gọi là đưa thừa số ra ngoài dấu căn. Ngược lại, ta có biến đổi đưa thừa số vào trong dấu căn. + Nếu \(a \ge 0\) thì \(a\sqrt b = \sqrt {{a^2}b} \). + Nếu \(a < 0\) thì \(a\sqrt b = - \sqrt {{a^2}b} \). |
Tổng quát, với hai biểu thức A và B mà \(B \ge 0\), ta có \(\sqrt {{A^2}B} = \left| A \right|\sqrt B \).
Ví dụ:
\(\sqrt {75} = \sqrt {25.3} = \sqrt {{5^2}.3} = 5\sqrt 3 \)
\(\sqrt {15a} .\sqrt {3a} = \sqrt {15a.3a} = \sqrt {{3^2}{a^2}.5} = \left| {3a} \right|\sqrt 5 \).
2. Căn thức bậc hai của một thương
Tính chất
Với biểu thức A nhận giá trị không âm và biểu thức B nhận giá trị dương, ta có \(\sqrt {\frac{A}{B}} = \frac{{\sqrt A }}{{\sqrt B }}\). |
Ví dụ: \(\sqrt {\frac{{49}}{{64}}} = \frac{{\sqrt {49} }}{{\sqrt {64} }} = \frac{7}{8}\);
\(\sqrt {\frac{{4{a^2}}}{{25}}} = \frac{{\sqrt {4{a^2}} }}{{\sqrt {25} }} = \frac{{\sqrt 4 .\sqrt {{a^2}} }}{{\sqrt {25} }} = \frac{{2\left| a \right|}}{5}\);
\(\frac{{\sqrt 8 }}{{\sqrt 2 }} = \sqrt {\frac{8}{2}} = \sqrt 4 = 2\);
Với \(a > 0\) thì \(\frac{{\sqrt {52{a^3}} }}{{\sqrt {13a} }} = \sqrt {\frac{{52{a^3}}}{{13a}}} = \sqrt {4{a^2}} = \sqrt {{{\left( {2a} \right)}^2}} = 2a\).
Nhận xét: Ta có thể biến đổi \(\sqrt {\frac{a}{b}} = \frac{{\sqrt a }}{{\sqrt b }}\) hoặc \(\frac{{\sqrt a }}{{\sqrt b }} = \sqrt {\frac{a}{b}} \) (\(a \ge 0\) và \(b > 0\)) để việc tính toán được dễ dàng hơn.
Phép khai phương là một trong những khái niệm quan trọng trong chương trình Toán 9, đặc biệt là trong chương trình Chân trời sáng tạo. Việc nắm vững lý thuyết và các tính chất của phép khai phương là nền tảng để giải quyết các bài toán liên quan một cách chính xác và hiệu quả.
Phép khai phương là phép toán ngược của phép bình phương. Cụ thể, nếu x2 = a (với a ≥ 0), thì x được gọi là căn bậc hai của a, ký hiệu là √a. √a là một số không âm sao cho bình phương của nó bằng a.
Dưới đây là các tính chất quan trọng của phép khai phương mà học sinh cần nắm vững:
Các tính chất của phép khai phương được sử dụng rộng rãi trong việc đơn giản hóa biểu thức, giải phương trình và chứng minh các đẳng thức. Dưới đây là một số ví dụ:
Ví dụ 1: Đơn giản biểu thức √(16 * 25). Áp dụng tính chất 2, ta có: √(16 * 25) = √16 * √25 = 4 * 5 = 20.
Ví dụ 2: Đơn giản biểu thức √(81/9). Áp dụng tính chất 3, ta có: √(81/9) = √81 / √9 = 9 / 3 = 3.
Để củng cố kiến thức, hãy thực hiện các bài tập sau:
Lý thuyết Tính chất của phép khai phương Toán 9 Chân trời sáng tạo là một phần quan trọng của chương trình học. Việc nắm vững các tính chất và biết cách vận dụng chúng vào giải toán sẽ giúp bạn đạt kết quả tốt trong các bài kiểm tra và kỳ thi. Hãy luyện tập thường xuyên để củng cố kiến thức và nâng cao kỹ năng giải toán của mình.