Giải bài tập 5 trang 92 SGK Toán 9 tập 2 - Chân trời sáng tạo

Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 9 tập 2. Bài viết này sẽ hướng dẫn bạn giải bài tập 5 trang 92 SGK Toán 9 tập 2 - Chân trời sáng tạo một cách nhanh chóng và hiệu quả.

Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, chúng tôi đã biên soạn lời giải chi tiết, kèm theo các bước giải rõ ràng, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.

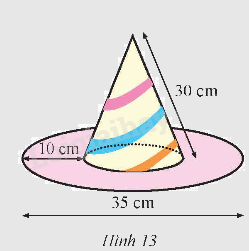
Một cái mũ chú hề có kích thước như Hình 13. Hãy tính tổng diện tích giấy làm nên chiếc mũ (không tính phần hao hụt, kết quả làm tròn đến hàng đơn vị).

Đề bài

Một cái mũ chú hề có kích thước như Hình 13. Hãy tính tổng diện tích giấy làm nên chiếc mũ (không tính phần hao hụt, kết quả làm tròn đến hàng đơn vị).

Giải bài tập 5 trang 92 SGK Toán 9 tập 2 - Chân trời sáng tạo 1

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết Giải bài tập 5 trang 92 SGK Toán 9 tập 2 - Chân trời sáng tạo 2

Dựa vào diện tích xung quanh của hình nón có bán kính r, độ dài đường sinh l là: \({S_{xq}} = \pi rl\)

Lời giải chi tiết

Diện tích phần làm nón là:

\({S_{xq}} = \pi rl = \pi .\left( {\frac{{35}}{2} - 10} \right).30 = 225\pi \) (cm²).

Diện tích phần làm vành mũ là:

\({S_{vanh}} = \pi {\left( {\frac{{35}}{2}} \right)^2} - \pi .{\left( {\frac{{35}}{2} - 10} \right)^2} = 250\pi \) (cm²).

Tổng diện tích để làm mũ là:

\({S_{xq}} + \) \({S_{vanh}} = 225\pi + 250\pi \approx \)1492 (cm²).

Làm chủ Toán 9, tự tin vào phòng thi! Đừng bỏ lỡ Giải bài tập 5 trang 92 SGK Toán 9 tập 2 - Chân trời sáng tạo đặc sắc thuộc chuyên mục sgk toán 9 trên nền tảng học toán. Với bộ bài tập lý thuyết toán thcs được biên soạn chuyên sâu, bám sát cấu trúc đề thi và chương trình sách giáo khoa mới nhất, đây chính là công cụ đắc lực giúp các em tối ưu hóa ôn luyện, củng cố kiến thức vững chắc và thuần thục mọi dạng bài thi khó nhằn. Phương pháp học trực quan, khoa học sẽ mang lại hiệu quả vượt trội, giúp con bạn chinh phục mọi thử thách một cách dễ dàng.

Giải bài tập 5 trang 92 SGK Toán 9 tập 2 - Chân trời sáng tạo: Hướng dẫn chi tiết

Bài tập 5 trang 92 SGK Toán 9 tập 2 - Chân trời sáng tạo thuộc chương trình học Toán 9, tập trung vào việc vận dụng kiến thức về hàm số bậc nhất và hàm số bậc hai để giải quyết các bài toán thực tế. Để giải quyết bài tập này một cách hiệu quả, chúng ta cần nắm vững các khái niệm cơ bản và các phương pháp giải toán liên quan.

Phần 1: Tóm tắt lý thuyết cần thiết

Trước khi đi vào giải bài tập, hãy cùng nhau ôn lại một số kiến thức lý thuyết quan trọng:

Hàm số bậc nhất: Hàm số có dạng y = ax + b (a ≠ 0). Đồ thị của hàm số là một đường thẳng.
Hàm số bậc hai: Hàm số có dạng y = ax² + bx + c (a ≠ 0). Đồ thị của hàm số là một parabol.
Cách xác định hệ số a, b, c: Dựa vào phương trình hàm số, ta có thể xác định các hệ số a, b, c.
Các yếu tố của hàm số bậc hai: Đỉnh của parabol, trục đối xứng, giao điểm với trục hoành và trục tung.

Phần 2: Phân tích bài tập 5 trang 92 SGK Toán 9 tập 2 - Chân trời sáng tạo

Bài tập 5 thường yêu cầu học sinh:

Xác định hàm số phù hợp với các điều kiện cho trước.
Vẽ đồ thị của hàm số.
Tìm các giá trị của x hoặc y thỏa mãn điều kiện cho trước.
Giải các bài toán ứng dụng liên quan đến hàm số.

Phần 3: Lời giải chi tiết bài tập 5 trang 92 SGK Toán 9 tập 2 - Chân trời sáng tạo

(Ở đây sẽ là lời giải chi tiết cho từng ý của bài tập 5, bao gồm các bước giải, giải thích rõ ràng và các lưu ý quan trọng. Ví dụ:)

Ví dụ: Giả sử bài tập yêu cầu tìm giao điểm của đường thẳng y = 2x + 1 và parabol y = x² - 3x + 2.

Bước 1: Cho hai phương trình bằng nhau: 2x + 1 = x² - 3x + 2
Bước 2: Chuyển vế và đưa về phương trình bậc hai: x² - 5x + 1 = 0
Bước 3: Giải phương trình bậc hai bằng công thức nghiệm: x = (5 ± √(25 - 4)) / 2 = (5 ± √21) / 2
Bước 4: Thay các giá trị x vừa tìm được vào một trong hai phương trình ban đầu để tìm giá trị y tương ứng.
Bước 5: Kết luận giao điểm của đường thẳng và parabol là ((5 + √21) / 2, y₁) và ((5 - √21) / 2, y₂).

Phần 4: Mở rộng và bài tập tương tự

Để củng cố kiến thức và rèn luyện kỹ năng giải toán, bạn có thể thử giải các bài tập tương tự sau:

Bài tập 6 trang 92 SGK Toán 9 tập 2 - Chân trời sáng tạo
Bài tập 7 trang 93 SGK Toán 9 tập 2 - Chân trời sáng tạo
Các bài tập trong sách bài tập Toán 9 tập 2

Phần 5: Lời khuyên và lưu ý khi giải bài tập về hàm số

Khi giải các bài tập về hàm số, bạn nên:

Đọc kỹ đề bài và xác định rõ yêu cầu của bài toán.
Vẽ đồ thị của hàm số để hình dung rõ hơn về bài toán.
Sử dụng các công thức và phương pháp giải toán phù hợp.
Kiểm tra lại kết quả để đảm bảo tính chính xác.

Hy vọng rằng với hướng dẫn chi tiết này, bạn sẽ tự tin hơn trong việc giải bài tập 5 trang 92 SGK Toán 9 tập 2 - Chân trời sáng tạo và các bài tập tương tự. Chúc bạn học tập tốt!