Giaitoan.edu.vn xin giới thiệu lời giải chi tiết mục 3 trang 65 SGK Toán 9 tập 1 - Chân trời sáng tạo. Bài viết này cung cấp đáp án đầy đủ, phương pháp giải rõ ràng, giúp học sinh nắm vững kiến thức và tự tin làm bài tập.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 9, đáp ứng nhu cầu học tập của học sinh trên toàn quốc.
a) Sử dụng máy tính cầm tay, tính tỉ số lượng giác của các góc sau (kết quả làm tròn đến hàng phần nghìn): 22o 52o 15o20’ 52o18’ b) Tìm các góc nhọn x, y, z, t trong mỗi trường hợp sau (kết quả làm tròn đến hàng phần trăm hoặc đến phút): sin x = 0,723 cos y = 0,828 tan z = 3,77 cot t = 1,54.
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 4 trang 65 SGK Toán 9 Chân trời sáng tạo
a) Sử dụng máy tính cầm tay, tính tỉ số lượng giác của các góc sau (kết quả làm tròn đến hàng phần nghìn):
22o
52o
15o20’
52o18’
b) Tìm các góc nhọn x, y, z, t trong mỗi trường hợp sau (kết quả làm tròn đến hàng phần trăm hoặc đến phút):
sin x = 0,723
cos y = 0,828
tan z = 3,77
cot t = 1,54.
Phương pháp giải:
- Dựa vào VD4 trang 64 làm tương tự.
- Dựa vào VD5 trang 65 làm tương tự.
Lời giải chi tiết:
a) \(\sin {52^o} \approx 0,375;\cos {22^o} \approx 0,927;\tan {22^o} \approx 0,404;\cot {22^o} \approx 2,745\)
\(\sin {52^o} \approx 0,788;\cos {52^o} \approx 0,616;\tan {52^o} \approx 1,28;\cot {52^o} \approx 0,781\)
\(\sin {15^o20’} \approx 0,264;\cos {15^o20’} \approx 0,964;\tan {15^o20’} \approx 0,274;\cot {15^o20’} \approx 3,647\)
\(\sin {52^o18’} \approx 0,791;\cos {52^o18’} \approx 0,612;\tan {52^o18’} \approx 1,294;\cot {52^o18’} \approx 0,773\)
b) Góc x \( \approx {46^o}18'\)
góc y \( \approx {34^o}6'\)
góc z \( \approx {75^o}8'\)
góc t \( \approx {32^o}59'\)
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 4 trang 65 SGK Toán 9 Chân trời sáng tạo
a) Sử dụng máy tính cầm tay, tính tỉ số lượng giác của các góc sau (kết quả làm tròn đến hàng phần nghìn):
22o
52o
15o20’
52o18’
b) Tìm các góc nhọn x, y, z, t trong mỗi trường hợp sau (kết quả làm tròn đến hàng phần trăm hoặc đến phút):
sin x = 0,723
cos y = 0,828
tan z = 3,77
cot t = 1,54.
Phương pháp giải:
- Dựa vào VD4 trang 64 làm tương tự.
- Dựa vào VD5 trang 65 làm tương tự.
Lời giải chi tiết:
a) \(\sin {52^o} \approx 0,375;\cos {22^o} \approx 0,927;\tan {22^o} \approx 0,404;\cot {22^o} \approx 2,745\)
\(\sin {52^o} \approx 0,788;\cos {52^o} \approx 0,616;\tan {52^o} \approx 1,28;\cot {52^o} \approx 0,781\)
\(\sin {15^o20’} \approx 0,264;\cos {15^o20’} \approx 0,964;\tan {15^o20’} \approx 0,274;\cot {15^o20’} \approx 3,647\)
\(\sin {52^o18’} \approx 0,791;\cos {52^o18’} \approx 0,612;\tan {52^o18’} \approx 1,294;\cot {52^o18’} \approx 0,773\)
b) Góc x \( \approx {46^o}18'\)
góc y \( \approx {34^o}6'\)
góc z \( \approx {75^o}8'\)
góc t \( \approx {32^o}59'\)
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 4 trang 65 SGK Toán 9 Chân trời sáng tạo
a) Vẽ một tam giác vuông có góc bằng 40o . Đo độ dài các cạnh rồi dùng các số đo để tính các tỉ số lượng giác của góc 40o . Kiểm tra lại các kết quả vừa tính bằng máy tính cầm tay.
b) Vẽ một tam giác vuông có ba cạnh bằng 3 cm, 4 cm, 5 cm. Tính các tỉ số lượng giác của mỗi góc nhọn. Dùng thức đo góc để đo các góc nhọn. Kiểm tra lại các kết quả bằng máy tính cầm tay.
Phương pháp giải:
Đọc kĩ dữ liệu đầu bài để vẽ hình, sử dụng:
+ Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin của góc \(\alpha \) , kí hiệu sin\(\alpha \).
+ Tỉ số giữa cạnh kề và cạnh huyền được gọi là côsin của góc \(\alpha \) , kí hiệu cos\(\alpha \).
+ Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của góc \(\alpha \) , kí hiệu tan\(\alpha \).
+ Tỉ số giữa cạnh kề và cạnh đối được gọi là côtang của góc \(\alpha \) , kí hiệu cot\(\alpha \).
Lời giải chi tiết:
a)
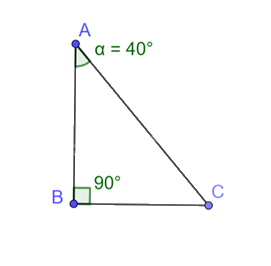
Các tỉ số lượng giác của góc \(\alpha \) là:
sin \(\alpha \) = \(\frac{{BC}}{{AC}} \approx 0,64\)
cos \(\alpha \) = \(\frac{{AB}}{{AC}} \approx 0,77\)
tan \(\alpha \) = \(\frac{{BC}}{{AB}} \approx 0,84\)
cot \(\alpha \) = \(\frac{1}{{\tan \alpha }} \approx 1,19\)
b)
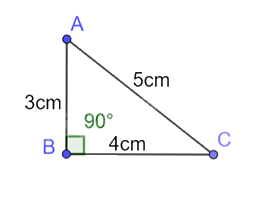
Các tỉ số lượng giác của góc \(\widehat {BAC}\) là:
sin \(\widehat {BAC}\) = \(\frac{{BC}}{{AC}} = \frac{4}{5}\)
cos \(\widehat {BAC}\) = \(\frac{{AB}}{{AC}} = \frac{3}{5}\)
tan \(\widehat {BAC}\) = \(\frac{{BC}}{{AB}} = \frac{4}{3}\)
cot \(\widehat {BAC}\) = \(\frac{1}{{\tan \alpha }} = \frac{3}{4}\)
Các tỉ số lượng giác của góc \(\widehat {ACB}\) là:
sin \(\widehat {ACB}\) = \(\frac{{AB}}{{AC}} = \frac{3}{5}\)
cos \(\widehat {ACB}\) = \(\frac{{BC}}{{AC}} = \frac{4}{5}\)
tan \(\widehat {ACB}\) = \(\frac{{AB}}{{BC}} = \frac{3}{4}\)
cot \(\widehat {ACB}\) = \(\frac{1}{{\tan \widehat {BAC}}} = \frac{4}{3}\)
Sử dụng thước đo góc, ta đo được \(\widehat {BAC} \approx 53^\circ\) và \(\widehat {ACB} \approx 37^\circ\). Kiểm tra lại các tỉ số lượng giác bằng máy tính cầm tay, ta thấy các giá trị bằng với giá trị mình viết phía trên.
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 4 trang 65 SGK Toán 9 Chân trời sáng tạo
a) Vẽ một tam giác vuông có góc bằng 40o . Đo độ dài các cạnh rồi dùng các số đo để tính các tỉ số lượng giác của góc 40o . Kiểm tra lại các kết quả vừa tính bằng máy tính cầm tay.
b) Vẽ một tam giác vuông có ba cạnh bằng 3 cm, 4 cm, 5 cm. Tính các tỉ số lượng giác của mỗi góc nhọn. Dùng thức đo góc để đo các góc nhọn. Kiểm tra lại các kết quả bằng máy tính cầm tay.
Phương pháp giải:
Đọc kĩ dữ liệu đầu bài để vẽ hình, sử dụng:
+ Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin của góc \(\alpha \) , kí hiệu sin\(\alpha \).
+ Tỉ số giữa cạnh kề và cạnh huyền được gọi là côsin của góc \(\alpha \) , kí hiệu cos\(\alpha \).
+ Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của góc \(\alpha \) , kí hiệu tan\(\alpha \).
+ Tỉ số giữa cạnh kề và cạnh đối được gọi là côtang của góc \(\alpha \) , kí hiệu cot\(\alpha \).
Lời giải chi tiết:
a)
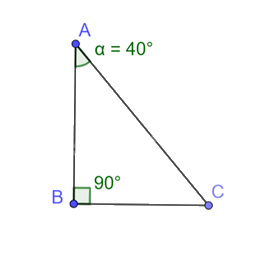
Các tỉ số lượng giác của góc \(\alpha \) là:
sin \(\alpha \) = \(\frac{{BC}}{{AC}} \approx 0,64\)
cos \(\alpha \) = \(\frac{{AB}}{{AC}} \approx 0,77\)
tan \(\alpha \) = \(\frac{{BC}}{{AB}} \approx 0,84\)
cot \(\alpha \) = \(\frac{1}{{\tan \alpha }} \approx 1,19\)
b)
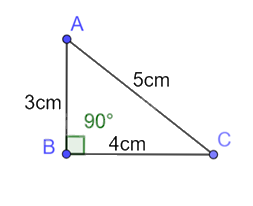
Các tỉ số lượng giác của góc \(\widehat {BAC}\) là:
sin \(\widehat {BAC}\) = \(\frac{{BC}}{{AC}} = \frac{4}{5}\)
cos \(\widehat {BAC}\) = \(\frac{{AB}}{{AC}} = \frac{3}{5}\)
tan \(\widehat {BAC}\) = \(\frac{{BC}}{{AB}} = \frac{4}{3}\)
cot \(\widehat {BAC}\) = \(\frac{1}{{\tan \alpha }} = \frac{3}{4}\)
Các tỉ số lượng giác của góc \(\widehat {ACB}\) là:
sin \(\widehat {ACB}\) = \(\frac{{AB}}{{AC}} = \frac{3}{5}\)
cos \(\widehat {ACB}\) = \(\frac{{BC}}{{AC}} = \frac{4}{5}\)
tan \(\widehat {ACB}\) = \(\frac{{AB}}{{BC}} = \frac{3}{4}\)
cot \(\widehat {ACB}\) = \(\frac{1}{{\tan \widehat {BAC}}} = \frac{4}{3}\)
Sử dụng thước đo góc, ta đo được \(\widehat {BAC} \approx 53^\circ\) và \(\widehat {ACB} \approx 37^\circ\). Kiểm tra lại các tỉ số lượng giác bằng máy tính cầm tay, ta thấy các giá trị bằng với giá trị mình viết phía trên.
Mục 3 trang 65 SGK Toán 9 tập 1 - Chân trời sáng tạo thường xoay quanh các bài toán liên quan đến hàm số bậc nhất, đồ thị hàm số và ứng dụng của hàm số trong thực tế. Việc nắm vững kiến thức về hàm số bậc nhất là nền tảng quan trọng để giải quyết các bài toán trong mục này.
Mục 3 thường bao gồm các dạng bài tập sau:
Để giải các bài toán trong Mục 3 trang 65 SGK Toán 9 tập 1 - Chân trời sáng tạo, học sinh cần:
Bài tập 1: Cho hàm số y = 2x - 3. Hãy xác định hệ số góc và tung độ gốc của hàm số.
Lời giải: Hàm số y = 2x - 3 có dạng y = ax + b, trong đó a là hệ số góc và b là tung độ gốc. Vậy, hệ số góc a = 2 và tung độ gốc b = -3.
Bài tập 2: Vẽ đồ thị hàm số y = -x + 1.
Lời giải:
Khi giải các bài tập trong Mục 3 trang 65 SGK Toán 9 tập 1 - Chân trời sáng tạo, học sinh cần lưu ý:
Hàm số bậc nhất có nhiều ứng dụng trong thực tế, ví dụ:
Mục 3 trang 65 SGK Toán 9 tập 1 - Chân trời sáng tạo là một phần quan trọng trong chương trình học Toán 9. Việc nắm vững kiến thức và kỹ năng giải các bài tập trong mục này sẽ giúp học sinh tự tin hơn trong các kỳ thi và ứng dụng toán học vào thực tế. Giaitoan.edu.vn hy vọng bài viết này đã cung cấp cho bạn những thông tin hữu ích và giúp bạn giải quyết các bài tập một cách hiệu quả.