Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 2 trang 99, 100 SGK Toán 9 tập 1 chương trình Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp đáp án chính xác, dễ hiểu cùng với phương pháp giải bài tập một cách khoa học và hiệu quả.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, tự tin giải quyết các bài toán Toán 9 và đạt kết quả cao trong học tập.
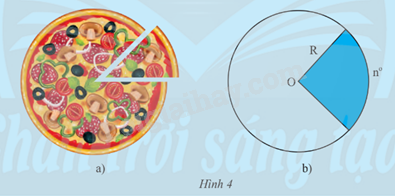
a) Ta có thể tính diện tích của miếng pizza trong Hình 4a theo góc ở tâm và bán kính của ổ bánh hay không? b) Chia một hình tròn bán kính R thành 360 phần bằng nhau. i) Tính diện tích mỗi phần đó. ii) Tính diện tích phần hình tròn ghép bởi n phần bằng nhau nó trên (Hình 4b).
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 2 trang 100 SGK Toán 9 Chân trời sáng tạo
Tính diện tích hình quạt tròn với bán kính R = 20 cm, ứng với cung 72o.
Phương pháp giải:
Dựa vào công thức hình quạt tròn: \(S = \frac{{\pi {R^2}n}}{{360}}\)
Lời giải chi tiết:
Hình quạt tròn với bán kính R = 20 cm, ứng với cung 72o có diện tích là:
\(S = \frac{{\pi {R^2}n}}{{360}} = \frac{{\pi {{.20}^2}.72}}{{360}} \approx 251,33\)(cm2)
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 2 trang 100 SGK Toán 9 Chân trời sáng tạo
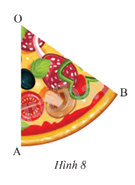
Tính diện tích của miếng bánh pizza có dạng hình quạt tròn trong Hình 8. Biết OA = 15 cm và \(\widehat {AOB} = {55^o}\).
Phương pháp giải:
Dựa vào công thức hình quạt tròn: \(S = \frac{{\pi {R^2}n}}{{360}}\)
Lời giải chi tiết:
Ta có độ dài cung AB = \(\widehat {AOB} = {55^o}\), bán kính R = 15 m có độ dài là:
\(S = \frac{{\pi {R^2}n}}{{360}} = \frac{{\pi {{.15}^2}.55}}{{360}} \approx 108\) cm2.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 99 SGK Toán 9 Chân trời sáng tạo
a) Ta có thể tính diện tích của miếng pizza trong Hình 4a theo góc ở tâm và bán kính của ổ bánh hay không?
b) Chia một hình tròn bán kính R thành 360 phần bằng nhau.
i) Tính diện tích mỗi phần đó.
ii) Tính diện tích phần hình tròn ghép bởi n phần bằng nhau nó trên (Hình 4b).
Phương pháp giải:
Dựa vào công thức diện tích hình tròn: S =\(\pi \)R2 .
Lời giải chi tiết:
a) Ta có thể tính diện tích của miếng pizza trong Hình 4a theo góc ở tâm và bán kính của ổ bánh.
b) i) Chia một hình tròn bán kính R thành 360 phần bằng nhau, diện tích mỗi phần đó là: \(\frac{{\pi {R^2}}}{{360}}\).
ii) diện tích phần hình tròn ghép bởi n phần bằng nhau là: \(n.\frac{{\pi {R^2}}}{{360}}\)
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 2 trang 99 SGK Toán 9 Chân trời sáng tạo
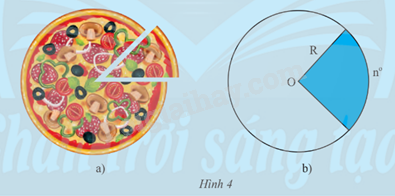
a) Ta có thể tính diện tích của miếng pizza trong Hình 4a theo góc ở tâm và bán kính của ổ bánh hay không?
b) Chia một hình tròn bán kính R thành 360 phần bằng nhau.
i) Tính diện tích mỗi phần đó.
ii) Tính diện tích phần hình tròn ghép bởi n phần bằng nhau nó trên (Hình 4b).
Phương pháp giải:
Dựa vào công thức diện tích hình tròn: S =\(\pi \)R2 .
Lời giải chi tiết:
a) Ta có thể tính diện tích của miếng pizza trong Hình 4a theo góc ở tâm và bán kính của ổ bánh.
b) i) Chia một hình tròn bán kính R thành 360 phần bằng nhau, diện tích mỗi phần đó là: \(\frac{{\pi {R^2}}}{{360}}\).
ii) diện tích phần hình tròn ghép bởi n phần bằng nhau là: \(n.\frac{{\pi {R^2}}}{{360}}\)
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 2 trang 100 SGK Toán 9 Chân trời sáng tạo
Tính diện tích hình quạt tròn với bán kính R = 20 cm, ứng với cung 72o.
Phương pháp giải:
Dựa vào công thức hình quạt tròn: \(S = \frac{{\pi {R^2}n}}{{360}}\)
Lời giải chi tiết:
Hình quạt tròn với bán kính R = 20 cm, ứng với cung 72o có diện tích là:
\(S = \frac{{\pi {R^2}n}}{{360}} = \frac{{\pi {{.20}^2}.72}}{{360}} \approx 251,33\)(cm2)
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 2 trang 100 SGK Toán 9 Chân trời sáng tạo
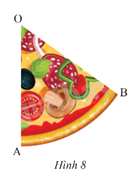
Tính diện tích của miếng bánh pizza có dạng hình quạt tròn trong Hình 8. Biết OA = 15 cm và \(\widehat {AOB} = {55^o}\).
Phương pháp giải:
Dựa vào công thức hình quạt tròn: \(S = \frac{{\pi {R^2}n}}{{360}}\)
Lời giải chi tiết:
Ta có độ dài cung AB = \(\widehat {AOB} = {55^o}\), bán kính R = 15 m có độ dài là:
\(S = \frac{{\pi {R^2}n}}{{360}} = \frac{{\pi {{.15}^2}.55}}{{360}} \approx 108\) cm2.
Mục 2 của chương trình Toán 9 tập 1 Chân trời sáng tạo thường tập trung vào các kiến thức về hàm số bậc nhất. Các bài tập trang 99 và 100 thường xoay quanh việc xác định hàm số, vẽ đồ thị hàm số, và ứng dụng hàm số vào giải quyết các bài toán thực tế. Việc nắm vững kiến thức nền tảng và luyện tập thường xuyên là chìa khóa để giải quyết tốt các bài tập này.
Để giúp các em hiểu rõ hơn về nội dung và phương pháp giải các bài tập trong mục 2 trang 99, 100 SGK Toán 9 tập 1 Chân trời sáng tạo, chúng ta sẽ đi vào phân tích từng bài tập cụ thể:
Bài tập này yêu cầu học sinh xác định các hệ số a và b của hàm số bậc nhất y = ax + b dựa vào các thông tin cho trước, chẳng hạn như đồ thị hàm số hoặc các điểm thuộc đồ thị hàm số. Để giải bài tập này, học sinh cần nắm vững các khái niệm về hệ số góc, giao điểm với trục tung, và cách xác định hàm số từ đồ thị.
Bài tập này yêu cầu học sinh vẽ đồ thị của hàm số bậc nhất y = ax + b. Để vẽ đồ thị, học sinh cần xác định ít nhất hai điểm thuộc đồ thị, sau đó nối chúng lại bằng một đường thẳng. Việc lựa chọn các điểm đặc biệt như giao điểm với trục tung và trục hoành sẽ giúp việc vẽ đồ thị trở nên dễ dàng hơn.
Bài tập này yêu cầu học sinh sử dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế, chẳng hạn như tính quãng đường đi được của một vật chuyển động đều, hoặc tính tiền lương dựa vào số giờ làm việc. Để giải bài tập này, học sinh cần phân tích đề bài, xác định các yếu tố liên quan đến hàm số, và xây dựng phương trình hàm số phù hợp.
Bài tập: Cho hàm số y = 2x - 1. Hãy xác định hệ số góc và giao điểm với trục tung của hàm số.
Giải:
Để học tốt môn Toán 9, các em cần dành thời gian ôn tập kiến thức cũ, làm bài tập đầy đủ, và tìm kiếm sự giúp đỡ của giáo viên hoặc bạn bè khi gặp khó khăn. Chúc các em học tập tốt và đạt kết quả cao!
| Công thức | Mô tả |
|---|---|
| y = ax + b | Hàm số bậc nhất |
| a | Hệ số góc |
| b | Giao điểm với trục tung |