Chào mừng các em học sinh đến với chuyên mục giải bài tập Toán 9 tập 2 của giaitoan.edu.vn. Ở bài viết này, chúng tôi sẽ cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 3 trang 8, 9, 10 sách giáo khoa Toán 9 tập 2 - Chân trời sáng tạo.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Cho hàm số (y = {x^2}). Ta lập bảng giá trị sau: x -3 -2 -1 0 1 2 3 (y = {x^2}) 9 4 1 0 1 4 9 Từ bảng trên, ta lấy các điểm A(-3;9), B(-2;4), C(-1;1), O(0;0), C’(1;1), B’(2;4), A’(3;9) trên mặt phẳng tọa độ Oxy. Đồ thị của hàm số (y = {x^2}) là một đường cong đi qua các điểm nêu trên và có dạnh như Hình 2. Từ đồ thị ở Hình 2, hãy trả lời các câu hỏi sau: a) Đồ thị của hàm số có vị trí như thế nào so với trục hoành? b) Có nhận xét gì về vị trí của các cặp điểm A và A’, B và B’, C và
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 3 trang 10 SGK Toán 9 Chân trời sáng tạo
Động năng (tính bằng J) của một quả bưởi nặng 1 kg rơi với tốc độ v (m/s) được tính bằng công thức \(K = \frac{1}{2}{v^2}\).
a) Tính động năng của quả bưởi đạt được khi nó rơi với tốc độ lần lượt là 3 m/s, 4 m/s.
b) Tính tốc độ rơi của quả bưởi tại thời điểm quả bưởi đạt được động năng 32 J.
Phương pháp giải:
Thay v lần lượt bằng 3, 4 vào công thức \(K = \frac{1}{2}{v^2}\) để tính.
Thay K = 32 J để tìm v.
Lời giải chi tiết:
a) Với v = 3 m/s ta có \(K = \frac{1}{2}{.3^2} = \frac{9}{2}\) J
Với v = 4 m/s ta có \(K = \frac{1}{2}{.4^2} = 8\)J
b) Với K = 32 J ta có: \(32 = \frac{1}{2}{v^2}\)
suy ra v2 = 64. Do đó, v = 8 (m/s).
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 3 trang 9 SGK Toán 9 Chân trời sáng tạo
Vẽ đồ thị hàm số y = 2x2.
Phương pháp giải:
Để vẽ đồ thị hàm số \(y = a{x^2}\left( {a \ne 0} \right)\), ta thực hiện các bước sau:
+ Lập bảng giá trị của hàm số với một số giá trị của x (thường lấy 5 giá trị gồm số 0 và hai cặp giá trị đối nhau).
+ Trên mặt phẳng tọa độ Oxy, đánh dấu các điểm (x;y) trong bảng giá trị (gồm điểm (0;0) và hai cặp điểm đối xứng nhau qua trục Oy).
+ Vẽ đường parabol đi qua các điểm vừa được đánh dấu.
Lời giải chi tiết:
Bảng giá trị:

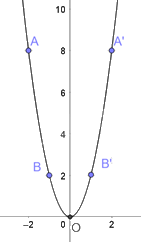
Trên mặt phẳng tọa độ, lấy các điểm A(-2;8), B(-1;2), O(0;0), B’(1;2), A’(2;8)
Đồ thị hàm số y = 2x2 là một đường parabol đỉnh O, đi qua các điểm trên và có dạng như dưới đây.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 4 trang 8 SGK Toán 9 Chân trời sáng tạo
Cho hàm số \(y = - \frac{3}{2}{x^2}\).
a) Lập bảng giá trị của hàm số khi x lần lượt nhận các giá trị -2; -1;0;1;2.
b) Vẽ đồ thị của hàm số. Có nhận xét gì về đồ thị của hàm số đó?
Phương pháp giải:
Thay lần lượt giá x vào hàm số \(y = - \frac{3}{2}{x^2}\)để tính y và lập bảng giá trị.
Từ bảng giá trị gọi các điểm và vẽ đồ thị là một đường cong đi qua các điểm trên.
Lời giải chi tiết:
a)
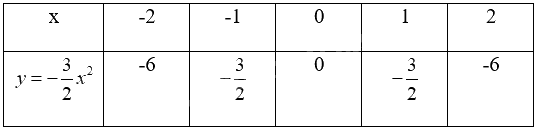
Lấy các điểm A(-2;6), B(-1; \( - \frac{3}{2}\)), O(0;0), B’(1; \( - \frac{3}{2}\)), A’(2;-6).
Đồ thị hàm số \(y = - \frac{3}{2}{x^2}\) là một đường cong đi qua các điểm nêu trên và có dạng như hình dưới.
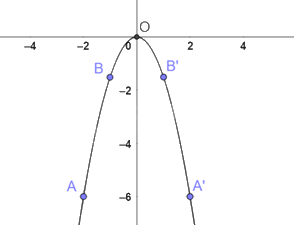
Nhận xét: Đồ thị nằm bên dưới trục hoành.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 3 trang 8 SGK Toán 9 Chân trời sáng tạo
Cho hàm số \(y = {x^2}\). Ta lập bảng giá trị sau:

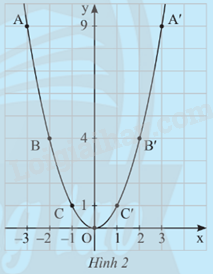
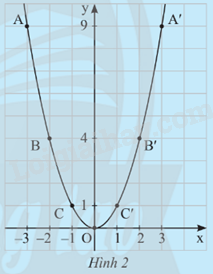
Từ bảng trên, ta lấy các điểm A(-3;9), B(-2;4), C(-1;1), O(0;0), C’(1;1), B’(2;4), A’(3;9) trên mặt phẳng tọa độ Oxy. Đồ thị của hàm số \(y = {x^2}\) là một đường cong đi qua các điểm nêu trên và có dạnh như Hình 2.
Từ đồ thị ở Hình 2, hãy trả lời các câu hỏi sau:
a) Đồ thị của hàm số có vị trí như thế nào so với trục hoành?
b) Có nhận xét gì về vị trí của các cặp điểm A và A’, B và B’, C và C’ so với trục tung?
c) Điểm nào là điểm thấp nhất của đồ thị?
Phương pháp giải:
Nhìn vào Hình 2 để nhận xét.
Lời giải chi tiết:
a) Đồ thị của hàm số có vị trí phía trên so với trục hoành.
b) Các cặp điểm A và A’, B và B’, C và C’ đối xứng với nhau qua trục tung.
c) Điểm thấp nhất của đồ thị là điểm O(0;0).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 3 trang 8 SGK Toán 9 Chân trời sáng tạo
Cho hàm số \(y = {x^2}\). Ta lập bảng giá trị sau:

Từ bảng trên, ta lấy các điểm A(-3;9), B(-2;4), C(-1;1), O(0;0), C’(1;1), B’(2;4), A’(3;9) trên mặt phẳng tọa độ Oxy. Đồ thị của hàm số \(y = {x^2}\) là một đường cong đi qua các điểm nêu trên và có dạnh như Hình 2.
Từ đồ thị ở Hình 2, hãy trả lời các câu hỏi sau:
a) Đồ thị của hàm số có vị trí như thế nào so với trục hoành?
b) Có nhận xét gì về vị trí của các cặp điểm A và A’, B và B’, C và C’ so với trục tung?
c) Điểm nào là điểm thấp nhất của đồ thị?
Phương pháp giải:
Nhìn vào Hình 2 để nhận xét.
Lời giải chi tiết:
a) Đồ thị của hàm số có vị trí phía trên so với trục hoành.
b) Các cặp điểm A và A’, B và B’, C và C’ đối xứng với nhau qua trục tung.
c) Điểm thấp nhất của đồ thị là điểm O(0;0).
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 4 trang 8 SGK Toán 9 Chân trời sáng tạo
Cho hàm số \(y = - \frac{3}{2}{x^2}\).
a) Lập bảng giá trị của hàm số khi x lần lượt nhận các giá trị -2; -1;0;1;2.
b) Vẽ đồ thị của hàm số. Có nhận xét gì về đồ thị của hàm số đó?
Phương pháp giải:
Thay lần lượt giá x vào hàm số \(y = - \frac{3}{2}{x^2}\)để tính y và lập bảng giá trị.
Từ bảng giá trị gọi các điểm và vẽ đồ thị là một đường cong đi qua các điểm trên.
Lời giải chi tiết:
a)
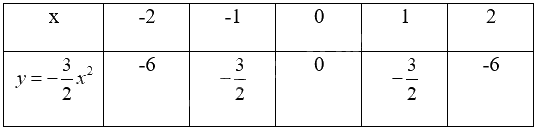
Lấy các điểm A(-2;6), B(-1; \( - \frac{3}{2}\)), O(0;0), B’(1; \( - \frac{3}{2}\)), A’(2;-6).
Đồ thị hàm số \(y = - \frac{3}{2}{x^2}\) là một đường cong đi qua các điểm nêu trên và có dạng như hình dưới.
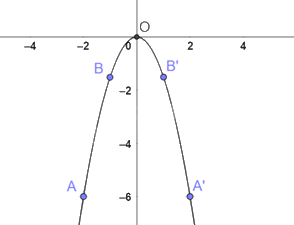
Nhận xét: Đồ thị nằm bên dưới trục hoành.
Video hướng dẫn giải
Trả lời câu hỏi Thực hành 3 trang 9 SGK Toán 9 Chân trời sáng tạo
Vẽ đồ thị hàm số y = 2x2.
Phương pháp giải:
Để vẽ đồ thị hàm số \(y = a{x^2}\left( {a \ne 0} \right)\), ta thực hiện các bước sau:
+ Lập bảng giá trị của hàm số với một số giá trị của x (thường lấy 5 giá trị gồm số 0 và hai cặp giá trị đối nhau).
+ Trên mặt phẳng tọa độ Oxy, đánh dấu các điểm (x;y) trong bảng giá trị (gồm điểm (0;0) và hai cặp điểm đối xứng nhau qua trục Oy).
+ Vẽ đường parabol đi qua các điểm vừa được đánh dấu.
Lời giải chi tiết:
Bảng giá trị:

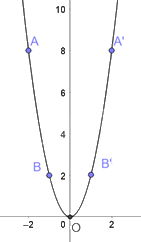
Trên mặt phẳng tọa độ, lấy các điểm A(-2;8), B(-1;2), O(0;0), B’(1;2), A’(2;8)
Đồ thị hàm số y = 2x2 là một đường parabol đỉnh O, đi qua các điểm trên và có dạng như dưới đây.
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 3 trang 10 SGK Toán 9 Chân trời sáng tạo
Động năng (tính bằng J) của một quả bưởi nặng 1 kg rơi với tốc độ v (m/s) được tính bằng công thức \(K = \frac{1}{2}{v^2}\).
a) Tính động năng của quả bưởi đạt được khi nó rơi với tốc độ lần lượt là 3 m/s, 4 m/s.
b) Tính tốc độ rơi của quả bưởi tại thời điểm quả bưởi đạt được động năng 32 J.
Phương pháp giải:
Thay v lần lượt bằng 3, 4 vào công thức \(K = \frac{1}{2}{v^2}\) để tính.
Thay K = 32 J để tìm v.
Lời giải chi tiết:
a) Với v = 3 m/s ta có \(K = \frac{1}{2}{.3^2} = \frac{9}{2}\) J
Với v = 4 m/s ta có \(K = \frac{1}{2}{.4^2} = 8\)J
b) Với K = 32 J ta có: \(32 = \frac{1}{2}{v^2}\)
suy ra v2 = 64. Do đó, v = 8 (m/s).
Mục 3 trong SGK Toán 9 tập 2 - Chân trời sáng tạo tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất. Các bài tập trong mục này yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, đồng thời rèn luyện kỹ năng tư duy logic và khả năng giải quyết vấn đề.
Bài 1 yêu cầu học sinh nhắc lại các khái niệm cơ bản về hàm số bậc nhất, bao gồm định nghĩa, dạng tổng quát, hệ số góc, và cách xác định hàm số.
Bài 2 yêu cầu học sinh xác định hàm số bậc nhất khi biết đồ thị của nó. Để làm được bài này, học sinh cần xác định được hai điểm thuộc đồ thị và sử dụng công thức tính hệ số góc.
Ví dụ: Cho đồ thị của hàm số đi qua hai điểm A(1; 2) và B(2; 4). Hãy xác định hàm số.
Bài 3 yêu cầu học sinh vẽ đồ thị của hàm số bậc nhất. Để vẽ đồ thị, học sinh cần xác định được ít nhất hai điểm thuộc đồ thị và nối chúng lại với nhau.
Ví dụ: Vẽ đồ thị của hàm số y = -x + 3
Bài 4 yêu cầu học sinh vận dụng kiến thức về hàm số bậc nhất để giải quyết các bài toán thực tế. Các bài toán này thường liên quan đến việc mô tả mối quan hệ giữa hai đại lượng bằng hàm số bậc nhất.
Ví dụ: Một người đi xe đạp với vận tốc 15 km/h. Hãy viết hàm số biểu thị quãng đường đi được của người đó theo thời gian.
Giải: Gọi x là thời gian đi (giờ) và y là quãng đường đi được (km). Ta có hàm số y = 15x
Hy vọng với lời giải chi tiết và hướng dẫn cụ thể trên đây, các em học sinh sẽ tự tin hơn khi giải các bài tập trong mục 3 trang 8, 9, 10 SGK Toán 9 tập 2 - Chân trời sáng tạo. Chúc các em học tập tốt!