Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 2 trang 95, 96 SGK Toán 9 tập 2 - Chân trời sáng tạo. Tại giaitoan.edu.vn, chúng tôi cung cấp các bài giải được trình bày rõ ràng, dễ hiểu, giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
Chúng tôi hiểu rằng việc học Toán đôi khi có thể gặp nhiều khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của chúng tôi đã biên soạn các lời giải chi tiết, kèm theo các ví dụ minh họa để giúp các em hiểu sâu sắc hơn về nội dung bài học.
Nhà khoa học cổ đại Archimèdes đã khám phá ra cách tính diện tích của mặt cầu như sau: Lấy một nửa hình cầu bán kính R và một hình trụ có bán kính đáy R. Dùng sợi dây quấn quanh nửa mặt cầu như Hình 10a, rồi cùng đoạn dây đó người ta quấn quanh hình trụ như Hình 10b thì thấy chiều cao của phần hình trụ được quấn dây bằng bán kính R. a) Tính theo R diện tích xung quanh của phần hình trụ được quấn dây ở Hình 10b. b) Từ đó dự đoán diện tích nửa mặt cầu ở Hình 10a.
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 2 trang 96 SGK Toán 9 Chân trời sáng tạo
Tìm diện tích bề mặt của Mặt Trăng, biết đường kính Mặt Trăng là khoảng
3474 km.
Phương pháp giải:
Dựa vào công thức tính diện tích mặt cầu là: S = \(4\pi {R^2}\)
Lời giải chi tiết:
Bán kính Mặt Trăng là: \(R = \frac{d}{2} = \frac{{3474}}{2}\) = 1737 km.
Diện tích bề mặt của Mặt Trăng là:
S = \(4\pi {R^2} = 4\pi .{(1737)^2} \approx \) 37914864 km2.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 3 trang 95SGK Toán 9 Chân trời sáng tạo
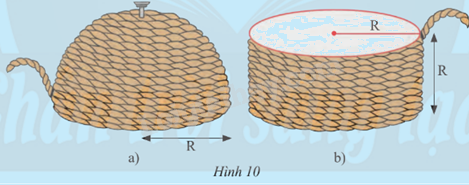
Nhà khoa học cổ đại Archimèdes đã khám phá ra cách tính diện tích của mặt cầu như sau: Lấy một nửa hình cầu bán kính R và một hình trụ có bán kính đáy R. Dùng sợi dây quấn quanh nửa mặt cầu như Hình 10a, rồi cùng đoạn dây đó người ta quấn quanh hình trụ như Hình 10b thì thấy chiều cao của phần hình trụ được quấn dây bằng bán kính R.
a) Tính theo R diện tích xung quanh của phần hình trụ được quấn dây ở Hình 10b.
b) Từ đó dự đoán diện tích nửa mặt cầu ở Hình 10a.
Phương pháp giải:
Dựa vào công thức tính diện tích xung quanh của hình trụ là: \({S_{xq}} = 2\pi rh\)
Lời giải chi tiết:
a) Diện tích xung quanh của phần hình trụ là: Scầu = Strụ = \(2\pi {R^2}\)
b) Diện tích nửa mặt cầu là: S = Strụ = \(2\pi {R^2}\)
Video hướng dẫn giải
Trả lời câu hỏi Vận dụng 2 trang 96 SGK Toán 9 Chân trời sáng tạo
Tìm diện tích bề mặt của Mặt Trăng, biết đường kính Mặt Trăng là khoảng
3474 km.
Phương pháp giải:
Dựa vào công thức tính diện tích mặt cầu là: S = \(4\pi {R^2}\)
Lời giải chi tiết:
Bán kính Mặt Trăng là: \(R = \frac{d}{2} = \frac{{3474}}{2}\) = 1737 km.
Diện tích bề mặt của Mặt Trăng là:
S = \(4\pi {R^2} = 4\pi .{(1737)^2} \approx \) 37914864 km2.
Video hướng dẫn giải
Trả lời câu hỏi Hoạt động 3 trang 95SGK Toán 9 Chân trời sáng tạo
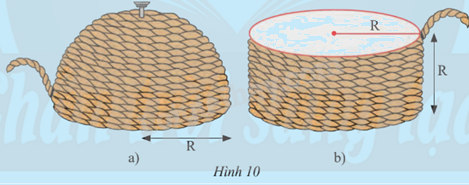
Nhà khoa học cổ đại Archimèdes đã khám phá ra cách tính diện tích của mặt cầu như sau: Lấy một nửa hình cầu bán kính R và một hình trụ có bán kính đáy R. Dùng sợi dây quấn quanh nửa mặt cầu như Hình 10a, rồi cùng đoạn dây đó người ta quấn quanh hình trụ như Hình 10b thì thấy chiều cao của phần hình trụ được quấn dây bằng bán kính R.
a) Tính theo R diện tích xung quanh của phần hình trụ được quấn dây ở Hình 10b.
b) Từ đó dự đoán diện tích nửa mặt cầu ở Hình 10a.
Phương pháp giải:
Dựa vào công thức tính diện tích xung quanh của hình trụ là: \({S_{xq}} = 2\pi rh\)
Lời giải chi tiết:
a) Diện tích xung quanh của phần hình trụ là: Scầu = Strụ = \(2\pi {R^2}\)
b) Diện tích nửa mặt cầu là: S = Strụ = \(2\pi {R^2}\)
Mục 2 của SGK Toán 9 tập 2 - Chân trời sáng tạo tập trung vào việc ôn tập và củng cố kiến thức về hàm số bậc nhất và hàm số bậc hai. Các bài tập trong mục này thường yêu cầu học sinh vận dụng các kiến thức đã học để giải quyết các bài toán thực tế, cũng như rèn luyện kỹ năng tư duy logic và phân tích.
Bài 1: (Trang 95) Cho hàm số y = 2x + 3. Tìm giá trị của x khi y = 5.
Lời giải: Thay y = 5 vào hàm số, ta có: 5 = 2x + 3. Giải phương trình này, ta được x = 1.
Bài 2: (Trang 95) Vẽ đồ thị của hàm số y = -x + 2.
Lời giải: Để vẽ đồ thị, ta cần xác định hai điểm thuộc đồ thị. Ví dụ, khi x = 0 thì y = 2, và khi x = 2 thì y = 0. Nối hai điểm này lại, ta được đồ thị của hàm số.
Bài 3: (Trang 96) Tìm giao điểm của hai đường thẳng y = x + 1 và y = -x + 3.
Lời giải: Để tìm giao điểm, ta giải hệ phương trình:
Bài 4: (Trang 96) Một người đi xe máy từ A đến B với vận tốc 40 km/h. Hỏi sau bao lâu người đó đến B, biết rằng quãng đường AB dài 120 km?
Lời giải: Thời gian người đó đi từ A đến B là: t = s/v = 120/40 = 3 giờ.
Để giải nhanh các bài tập về hàm số, các em cần nắm vững các công thức và tính chất cơ bản của hàm số. Ngoài ra, các em cũng nên luyện tập thường xuyên để rèn luyện kỹ năng giải toán và làm quen với các dạng bài tập khác nhau.
Hàm số có rất nhiều ứng dụng trong thực tế, ví dụ như trong việc dự báo thời tiết, tính toán chi phí sản xuất, và phân tích dữ liệu kinh tế. Việc hiểu rõ về hàm số sẽ giúp các em có thể áp dụng kiến thức đã học vào việc giải quyết các vấn đề thực tế.
Hy vọng rằng với lời giải chi tiết và hướng dẫn giải bài tập trong mục 2 trang 95, 96 SGK Toán 9 tập 2 - Chân trời sáng tạo, các em học sinh sẽ hiểu rõ hơn về nội dung bài học và tự tin giải các bài tập tương tự. Chúc các em học tập tốt!